Нарушение какого-либо из условий теоремы Коши в какой-нибудь точке может привести к тому, что через точку 
может не проходить ни одна интегральная кривая уравнения, а могут проходить несколько интегральных кривых.
Изолированные точки плоскости, в которых нарушается существование или единственность решения данного дифференциального уравнения, называется особыми точками этого уравнения.
Особые решения не могут быть получены из формулы общего решения ни при каком значении постоянной С. (см. пример, Вулих, стр. 289).
Заметим, что условия теоремы Коши являются лишь достаточными, но не необходимыми. Поэтому особые точки дифференциального уравнения
Следует искать среди точек разрыва функции 
и точек, где не существует производная 
; однако все такие точки не обязательно должны быть особыми.
Пример. Для уравнения 
общим решением является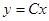 
, т.е. семейство всех прямых, проходящих через начальные координаты. Особая точка при х=0, т.е. (если х=0, то 
не существует; из выражения 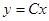получим y=0 при x=0) точка (0;0)
Интегрирование некоторых типов дифференциальных уравнений первого порядка
1. Интегрирование уравнений с разделяющимися переменными
а) Простейшим дифференциальным уравнением первого порядка является уравнение в форме, разрешенной относительно производной, и не содержащее у:
(1)
Как известно из курса интегрального исчисления, в этом случае для нахождения неизвестной функции y достаточно найти неопределенный интеграл от функции 
. Общее решение уравнения (1) запишется в виде:
Замечание: Здесь и всюду в дальнейшем символ 
будет означать какую-либо одну первообразную функцию.
Пример: Найти частное решение дифференциального уравнения 
, удовлетворяющее начальному условию 
.
Решение: Интегрирую, получаем общее решение 
. Для нахождения частного решения положим в общем решении x=1, y=2 и определим, что C=1. Следовательно, искомое частное решение имеет вид: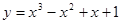 
Ответ. 
б) Пусть дано дифференциальное уравнение:
(2)
Где в правой части стоит произведение функции, зависящей только от х, на функцию, зависящую только от у. Такое уравнение называется уравнением с разделяющимися переменными. Пусть 
. В уравнении (2) заменим 
на 
: 
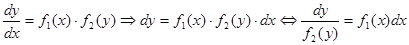(3)
В уравнении (3) переменные х и у отделены друг от друга. Равенство (3) можно рассматривать как равенство двух дифференциалов:
Но если дифференциалы двух функций равны, то сами функции отличаются разве лишь на постоянное слагаемое:
Это равенство дает общее решение данного уравнения. Следовательно, для решения уравнения (3) надо взять интегралы от обеих частей уравнения, ибо производя интегрирование получим искомую зависимость у от х, освобожденную от их дифференциалов.
Уравнение (3) называется уравнением с разделенными переменными.
Пример: Найти общий интеграл уравнения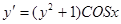 
.
Решение: Данное уравнение есть уравнение с разделяющимися переменными. Здесь 
. Эти функции всюду непрерывны, 
. Разделяя переменные, получим: 
. Интегрирую, находим: 
, или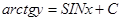 
- общий интеграл рассматриваемого дифференциального уравнения.
в) В общем случае можно дать такое определение.
Уравнением с разделяющимися переменными называется уравнение вида P(x)M(y)dx+Q(x)N(y)dy=0 (4)
Название уравнения объясняется тем, что в таком уравнении можно «отделить» переменные х и у друг от друга, уединив все члены с переменной х и dx в одной части уравнения, а все члены с переменной у и dy - в другой.
Для этого надо поделить левую часть уравнения (4) на M(y)Q(x) (помня при этом указания относительно возможного нарушения равносильности уравнений).
Замечание. При делении обеих частей уравнения на M(y)Q(x) должны помнить, что это преобразование законно производить только в той области, где ни M(y), ни Q(x) не обращаются в нуль.
Поделив получим:
По доказанному выше общий интеграл этого уравнения равен:
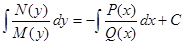, или 
.
Замечание. Можно было записать (см. Вулих, стр. 292) без произвольной постоянной С, включив ее в состав неопределенных интегралов.
Таким образом, отыскание общего интеграла уравнения свелось к интегрированию.
Замечание. При решении уравнений с разделяющимися переменными нужно находить и особые решения, если они есть.
Пример 1. Найти общий интеграл дифференциального уравнения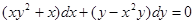 
.
Решение. 
С целью получения более удобной формы записи решения в качестве произвольной постоянной взяли 
, что не нарушает общности рассуждений.
Итак, общий интеграл данного дифференциального уравнения определяет семейство кривых второго порядка (семейство гипербол и элипсов, а при 
- мнимых элипсов).
Пример 2. (Физический пример)
Для очистки газа от некоторой газообразной же примеси его пропускают через скруббер (сосуд, содержащий тот или иной поглотитель). Количество газообразной примеси, поглощаемое тонким слоем поглотителя при установившемся режиме аппарата, пропорционально концентрации примеси, а также толщине и площади поперечного сечения слоя. Скруббер имеет форму конуса с радиусом основания R и высотой H. Газ поступает через вершину конуса. Найти зависимость концентрации газообразной примеси в скруббере как функцию расстояния слоя от вершины конуса, если концентрация примеси в поступающем газе равна a%, а в выходящем b%.
Решение.
 |
h
r
H dh
R
Обозначим: q% - концентрация примеси; h - расстояние слоя от вершины конуса; r - радиус сечения тонкого слоя конуса.
Составим дифференциальное уравнени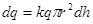е: 
, где 
.
Следовательно,
Так как q=a при h=0, то c=a и, следовательно, 
Найдем к: при h=H q=b, имеем 
.
Окончательно получим: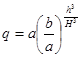 
2. Уравнения, приводящиеся к уравнениям с разделяющимися переменными.
Дифференциальные уравнения вида 
, где 
приводятся к уравнениям с разделяющимися переменными при помощи замены 
, где z – новая искомая функция (от аргумента х).
В случае b=0 сразу получим уравнение с разделяющимися переменными.
Произведем замену неизвестной функции у новой функцией z:
Интегрируя, получим общий интеграл этого уравнения: 
Пример.
Решить уравнение 
.
Решение. Положим z=y-x, y=z+x, 
. Подставляем в уравнение:
Кроме того решениями уравнения будут функции, которые получаем так: 
, откуда 
.
Пример. (Демидович, 2752)
Найти общий интеграл уравнения 
.
Решение. Введем новую переменную z, обозначим z=8x+2y+1, 
, 
, подставим в уравнение: 
Ответ: 
3. Интегрирование однородных уравнений
Уравнение, однородное относительно x и y, легко сводится к уравнению с разделяющимися переменными с помощью замены переменной.
Опредeление. Функция f(x,y) называется однородной функцией нулевого измерения, если при умножении аргументов x и y на произвольный параметр значение функции не измеряется, т.е. f(kx,ky)=f(x,y).
Например, функция 
- однородная функция нулевого измерения.
Покажем, что всякую функцию однородную нулевого измерения можно представить в виде функции отношения 
: доказано, пусть f(x,y) – однородная функция нулевого измерения. Пользуясь тем, что параметр можно выбрать произвольным, положим (параметр) 
. Тогда 
.
Определение. Уравнение 
называется однородным относительно x, y, если функция f(x,y) является однородной функцией нулевого измерения.
Таким образом, однородное уравнение можно записать в виде: 
, положим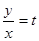 
, откуда 
. Подставим в уравнение: 
- получим уравнение с разделяющимися переменными 
, разделим переменные: 
Подставив после интегрирования вместо t отношение , получим общий интеграл дифференциального уравнения 
.
В общем случае можно дать такое определение.
Определение. Функция f(x,y) называется однородной функцией n-го измерения, если при любом k выполняется равенство 
Показатель степени “n” называется измерением (или степенью) однородности функции.
Например, функция 
- однородная функция третьего измерения.
Уравнение 
, в котором функции 
и 
- однородные функции одного и того же измерения, также является дифференциальным уравнением, однородным относительно х и у.
Доказано, из этого уравнения 
, а отношение 
будет однородной функцией нулевого измерения.
Пример. Решить уравнение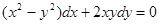 
. В приведенных выше обозначениях 
, 
. Обе функции – однородные второго измерения (т.е. одного и того же измерения). Следовательно, данное уравнение однородное. Вводим новую функцию t, положив 
Сокращаем на 
.
Вывод. Итак, решение однородного уравнения первого порядка проводится путем введения новой переменной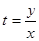 
, с помощью которой уравнение превращается в уравнение с разделяющимися переменными.
Замечание. Некоторые однородные уравнения проще решаются с помощью подстановки 
, которая, как легко убедится, также приводит однородное уравнение к уравнению с разделяющимися переменными.
Пример. 
4. Уравнения, приводящиеся к однородным.
К однородным уравнениям можно привести уравнения вида 
(1)
Замечание. При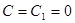 
уравнение (1), очевидно, есть однородное. Поэтому будем полагать, что хотя бы одно из них не равно нулю.
Сделаем замену переменных по формулам:
(2)
Числа 
и 
подберем так, чтобы уравнение (1) стало однородным. При указанной замене 
. Уравнение (1) принимает вид:
(*)
Чтобы последнее уравнение стало однородным, надо, чтобы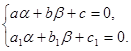 
(3)
Решая систему (3), определим и . Уравнение (*) перепишется так: 
- это однородное уравнение.
Замечание. Указанный прием неприменим в тех случаях, когда система уравнений (3) для нахождения и несовместна.
Это получается тогда, когда коэффициенты при х и у в числителе и знаменателе уравнения (1)пропорциональны: 
.
В таком случае надо вводить новую переменную z по формуле z=ax+by. Получится (после такой подстановки) уравнение с разделяющимися переменными x,y.
Пример. Решить уравнение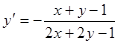 
(1)
Решение. Коэффициенты при x и y пропорциональны, поэтому новую переменную вводим по формуле 
Разделяем переменные: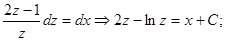 
; заменяем z:
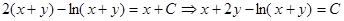
5. Линейные уравнения первого порядка
Определение. Дифференциальное уравнение называется линейным, если оно линейно (т.е. первой степени) относительно искомой функции у и ее производной 
.
Общий вид линейного уравнения первого порядка
(1)
где 
- непрерывные функции или постоянные.
Если правая часть уравнения (1) f(x)=0, то уравнение называется линейным однородным; в противном случае оно называется неоднородным (или уравнением с правой частью).
Пусть 
. приведем 2 способа интегрирования этого уравнения. (При f(x)=0 уравнение (1) одновременно является уравнением с разделяющимися переменными, поэтому не требует специального рассмотрения).
1. Способ подстановки.
Произведем в уравнении (1) замену переменной, положив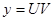 
.
Вычислим: 
.
Уравнение примет вид: 
.(2)
До сих пор мы не делали никаких предположений относительно U и V. теперь наложим условие на один из множителей (U и V,) а именно, предположим, что функция 
такова, что она обращает в тождественный нуль выражение, стоящее в квадратных скобках, т.е. что она является решением дифференциального уравнения 
(3)
Это есть уравнение с разделяющимися переменными из него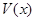 
:
Замечание. Нам достаточно найти только одно решение уравнения (3), поэтому в последней формуле берем за функцию 
(т.е. постоянную интегрирования С не пишем).
Очевидно, что 
, поэтому условие (3), наложенное на функцию V, не противоречит равенству y=UV. Доказано, любую величину можно представить в виде произведения двух сомножителей, из которых один отличен от нуля.
Найдя функцию V(x), переходим к размыканию функции U(x). Она должна быть такой, чтобы при найденной функции V произведение UV было решением уравнения (2). Для этого надо, чтобы U(x) была решением уравнения 
(4)
(это то, во что обращается уравнение (2) при подстановке туда вместо V(x) найденного для этой функции выражения).
В уравнении (4) переменные также разделяются:
(5)
Найденные функции U(x), V(x) подставляем в формулу y=UV, получим общее решение линейного уравнения(1):
(6)
Вывод. Таким образом, указанный прием (способ Бернулли) сводит решение линейного уравнения (1) к решению двух уравнений (3) и (4) с разделяющимися переменными.
Замечание 1. Линейное уравнение (1) не имеет особых решений (что видно из самого вывода формулы (6) – см. Вулих, стр. 302)
Замечание 2. При решении примеров не следует пользоваться готовой формулой (6), а надо находить постепенно функции U(x) и V(x), также как это было сделано в общем случае.
Пример. Найти частное решение уравнения 
, удовлетворяющее начальным условиям: y(2)=1.
Решение.
Cледовательно, 
Так как при х=2, у=1, то 
Ответ. у=1.
2. Способ вариации произвольной постоянной (метод Лагранжа)
3.
Вместо того, чтобы искать решение неоднородного уравнения (1), где 
, решим сначала соответствующее ему однородное уравнение
(7)
которое является уравнением с разделяющимися переменными. Его общее решение получается таким образом:
где С – произвольная постоянная.
Совершенно очевидно, что найденная функция у не может быть решением неоднородного уравнения.
Будем рассматривать С не как произвольную постоянную, а как некоторую функцию от х, т.е. С=С(х), то оказывается, что можно подобрать функцию С(х) так, чтобы функция (8) стала решением неоднородного уравнения (1).
Для нахождения функции С(х) вычислим производную функции 
(9), подставим выражения 
и в уравнение (1) и потребуем, чтобы оно при этом удовлетворялось, т.е. обратилось в тождество:
Производная неопределенного интеграла равна подынтегральной функции.
Это есть уравнение с разделяющимися переменными и неизвестной функцией С(х).
Подставляя найденное выражение С(х) в равенство (9), получим искомое решение неоднородного уравнения (1) снова в виде (6):
Замечание. Название способа происходит от того, что мы варьируем (изменением) произвольную постоянную С, считая ее функцией от х.
Этот способ, как и способ подстановки, позволяет свести линейное уравнение (1) к двум уравнениям с разделяющимися переменными.
Замечание. Нет необходимости запоминать формулу (6). Целесообразнее помнить лишь сам приведенный способ решения уравнения (10 и применять его в каждом конкретном случае заново.
Пример 1. Решить уравнение 
.
Решение. Данное уравнение является линейным относительно х и 
. Преобразуем его к нормальному виду:
а) Интегрируем соответствующее однородное уравнение:
б) Считаем «С» функцией от «у»; тогда 
Подставляя в заданное уравнение, найдем:
где С – произвольная постоянная.
Следовательно, 
.
Задача (Уваров, т. 2, стр. 396) – на линейное уравнение.
В электрической цепи (см. рис.), имеющей сопротивление R и индуктивность L, сила тока возбуждается электродвижущей силой E. Найти зависимость силы тока I (при установившемся режиме) от времени t, зная, что в момент времени t=0 она равна нулю.
Решение. Из физики известно, что потеря напряжения на сопротивлении в момент времени t равна RI(t), а потеря напряжения на индуктивности в этот момент равна 
.
По закону Кирхгофа в каждый момент времени t сумма потерь напряжений на всех участках цепи равна действующей активной электродвижущей силе.
Следовательно, функция I(t) подчиняется дифференциальному уравнению 
R и L- постоянные E=const.
- это линейное дифференциальное уравнение
Подставляя в неоднородное уравнение:
Следовательно, 
(*).
Определяем С из начального условия: I(0)=0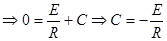 
Искомое частное решение будет: 
Пример: 
Решение: 
6. Уравнение Бернулли
Общий вид уравнения Бернулли 
, где P(x) и f(x) – заданные непрерывные функции от х (или постоянные), а n=const; 
.
При n=0 уравнение Бернулли переходит в линейное уравнение; при n=1 оно является уравнением с разделяющимися переменными, так как может быть преобразовано к виду: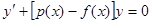 
и, следовательно, может быть проинтегрировано разделением переменных.
Уравнение Бернулли можно соответствующей подстановкой привести к линейному уравнению. Для этого разделим обе части уравнения на 
:
Положим 
,т.е. 
. Тогда 
.
Уравнение Бернулли принимает вид:
Это линейное уравнение первого порядка с неизвестной функцией z; решив его, находим функцию z от x. Возвращаясь к первоначальной переменной у путем обратной замены z на 
, получим общий интеграл уравнения Бернулли.
Кроме того, решением любого дифференциального уравнения Бернулли при 
является функция y=0, не получаемая из общего решения.
Таким образом, уравнение Бернулли сводится к линейному уравнению подстановкой 
.
Замечание. При решении уравнения Бернулли практически нет необходимости предварительно преобразовывать его в линейное; уравнение Бернулли можно интегрировать непосредственно теми же методами, что и линейное, минуя промежуточный этап – сведение к линейному уравнению.
Пример (Демидович, стр. 2792).
Найти общее решение уравнения
Решение. Здесь n=2, делим обе части уравнения на 
: 
.
Вводим новую переменную 
.
Уравнение принимает вид: 
.
Мы получили линейное неоднородное уравнение:
Общий интеграл дифференциального уравнения.
Задача. Составить уравнение кривой, проходящей через начало координат, зная, что середина отрезка ее нормали от любой точки кривой до оси Ox находится на параболе 
.
Решение.
y y
M(x,y) M(x,y)
N N
P x P(X,0) x
0 0
Возьмем на кривой произвольную точку M(x,y). Проведем нормаль к кривой в точке М; точка Р – точка пересечения нормали к кривой в т. М с осью Ox.
N - середина отрезка MP нормали. (см. чертеж)
Найдем координаты точки P: уравнение искомой кривой y=f(x); уравнение нормали к ней в точке М(x,y) имеет вид: 
, но ордината точки Р равна о; поэтому имеем 
Уравнение нормали к кривой: 
Найдем координаты точки N:
N - середина MP
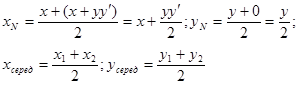
Но точка 
параболе , поэтому ее координаты удовлетворяют уравнению параболы:
(разделим на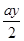 
)
- это уравнение Бернулли (n=-1)
Пусть 
Начальное условие: y=0 при x=0;
Оно позволяет найти 
.
Уравнение искомой линии имеет вид
7. Уравнение в полных дифференциалах
Рассмотрим дифференциальное уравнение первого порядка в симметричной относительно х и у дифференциальной форме:
(1)
Может случится, что левая часть уравнения (1) будет полным дифференциалом некоторой функции F(x,y), т.е. 
Определение. Уравнение 
, где левая часть представляет собой полный дифференциал некоторой функции двух переменных, называется уравнением в полных дифференциалах.
Такое уравнение может быть переписано в виде:
(2)
откуда интегрированием получаем общий интеграл F(x,y)=C.
Естественно, возникает вопрос: при каких условиях уравнение (1) представляет собой уравнение в полных дифференциалах dF(x,y)=0 и как найти функцию F(x,y)?
Ответом на этот вопроса служит следующая теорема:
Пусть для того чтобы выражение 
(*), где функции P(x,y) и Q(x,y) определены и непрерывны в области Д плоскости Oxy и имеют в ней непрерывные частные производные 
и 
, представляло собой полный дифференциал некоторой функции F(x,y), необходимо и достаточно, чтобы во всех точках области Д выполнялось условие: 
(3)
А) Необходимость. Предположим, что 
такая функция F(x,y), что 
. (4). Докажем, что имеет место равенство (3). Известно, что 
. Так как оно равно выражению (4), то имеем тождество:
Справедливое для любых dx и dy.
Сравнивая множители при dx и dy, получим:
Продифференцируем обе части первого равенства по y, а второго – по x; имеем:
Из равенства смешанных производных (см. теорему Шварца) заключаем, что
(3)
б) Достаточность. Пусть условие (3) выполняется. Докажем, что выражение (*) представляет собой полный дифференциал некоторой функции F(x,y), т.е., что справедливы равенства: 
(5)
(т.е. задача сводится к отысканию функции F(x,y)).
Возьмем первое из уравнений (5): 
;
Интегрируем его по переменной х:
(6)
где 
– абсцисса какой-либо точки М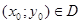 
- произвольная функция от у, заменяющая произвольную постоянную С (поскольку интегрирование производится по х в предположении, что у сохраняет неизменное значение).
Определим 
так, чтобы удовлетворялось и второе из уравнений (5): продифференцируем обе части равенства (6) по у; тогда получим
Но так как (см. равенства (5)) 
, то имеем 
.
По теореме о дифференцировании определенного интеграла по параметру
Поэтому имеем:
По условию 
(интегрируем это равенство по у)
Подставим значение в равенство (6):
Вывод: Итак, не только доказано существование функции F(x,y), но и выведена формула для нахождения этой функции.
Замечание. При решении соответствующих уравнений можно не пользоваться готовой формулой, а поступать таким же образом, как в общем случае (или с заменой определенных интегралов неопределенными).
Пример. Найти частный интеграл уравнения 
, удовлетворяющий начальному условию y(1)=e.
Решение.
Следовательно, это уравнение является уравнением в полных дифференциалах
Общий интеграл уравнения: 
(т.к. нет необходимости оставлять в записи две постоянные, то лучше их объединить в одну); или 
.
Найдем частный интеграл: y=e при х=1
Ответ.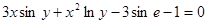 
Пример (Шестаков, стр. 140)
«Дифференциальные уравнения высших порядков»
Основные понятия
Все дифференциальные уравнения порядка выше первого называются дифференциальными уравнениями высших порядков.
Уравнение n-го порядка, кроме производной 
, может содержать также и младшие производные, так что общий вид такого уравнения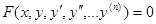 
(1), или, если это возможно, в форме, разрешенной относительно старшей производной:
(2)
Как и для уравнения первого порядка, общее решение будет зависеть от произвольных постоянных.
Для уравнения первого порядка таким дополнительным условием являлось задание значения 
,т.е. координат точки, через которую проходит интегрированная кривая.
Для уравнений высших порядков эти условия можно задавать различными способами.
Например, для уравнения второго порядка общее решение, как будет указано далее, зависит от двух произвольных постоянных. Для нахождения их значений нужно иметь два условия. Их можно получить, задав значения искомой функции в двух точках или иначе, задав в одной точке значения искомой функции и ее производной (первой).
Второй способ имеет широкое распространение при решении дифференциальных уравнений, к которым приводятся задачи механики. Доказано, если пользоваться терминами механики, то речь идет об отыскании закона движения, причем задано начальное положение точки (значение функции) и ее начальная скорость (первая производная).
Для уравнений порядка n в качестве начальных условий задаются в некоторой точке значения искомой функции и всех ее производных до (n-1)-го порядка включительно, т.е. при 
(3)
Систему чисел (3) называют системой начальных условий.
Задачу нахождения частного решения дифференциального уравнения (2), удовлетворяющего системе начальных условий (3), называют задачей Коши.