Теорема. Пусть дано дифференциальное уравнение (2):
И система начальных условий (3).
Если функция 
непрерывна в окрестности начальных условий и имеет непрерывные частные производные по аргументам 
, то существует, и притом единственное, решение уравнения, определенное и непрерывное в некотором интервале, содержащем 
, и удовлетворяющее заданной системе начальных условий.
На доказательстве этой теоремы мы останавливаться не будем.
В сопротивлении материалов часто бывает необходимость отыскать частное решение, если известны значения искомой функции в нескольких точках.
Такие же задачи или несколько более общие встречаются и в других областях, требующих применения дифференциальных уравнений.
Во многих из этих задач частные решения приходится находить из условий другого рода, которые принято называть граничными или краевыми.
Такие задачи являются, вообще говоря, более сложными, нежели задачи с начальными условиями.
Определение. Общим решением дифференциального уравнения (2) называется решение, содержащее произвольные постоянные, которые можно подобрать таким образом, чтобы удовлетворить любой допустимой системе начальных условий.
Общее решение уравнения n-го порядка зависит от n произвольных постоянных:
Иногда общее решение для уравнения (2) задается в неявной форме, т.е. определяется соотношением вида
Его называют общим интегралом уравнения (2)
Задача интегрирования дифференциальных уравнений высших порядков является значительно более сложной, нежели задача интегрирования уравнения первого порядка.
Интегрирование некоторых дифференциальных уравнений путем понижения порядка
Для некоторых типов дифференциальных уравнений высших порядков можно применить метод интегрирования путем понижения порядка, т.е. сведение путем замены переменных данного уравнения к другому, имеющему порядок ниже заданного.
Рассмотрим несколько простейших видов дифференциальных уравнений, допускающих понижение порядка.
Будем изучать их на примере уравнений второго порядка.
Дифференциальное уравнение второго порядка имеет вид
,
либо 
. Их общее решение (общий интеграл) зависит от двух произвольных постоянных.
Дифференциальное уравнение не содержит явно искомой функции, т.е. имеет вид
Введем новую переменную z, положив 
.
Тогда 
и уравнение (1) превращается в уравнение первого порядка с искомой функцией z:
Решаем это уравнение первого порядка (если оно интегрируемо в конечном виде), получим общее решение в виде
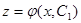
Заменяя z через 
, получаем:
Итак, общее решение 
содержит уже две произвольных постоянных.
Пример 1. 
- это и есть линейное уравнение первого порядка
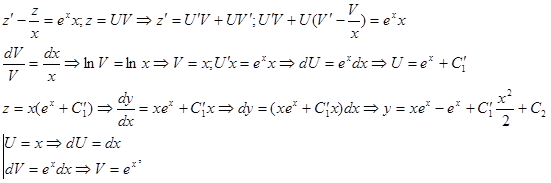
Ответ.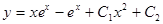 
Задача. Подводная лодка массы m без начальной скорости медленно погружается в воду, причем известно, что при таком погружении сила сопротивления воды пропорциональна скорости погружения (коэффициент пропорциональности равен k). Найти путь, пройденный лодкой за время t.
Решение.F –величина силы, действующей на лодку;
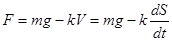
С другой стороны, по второму основному закону динамики; 
и мы имеем следующее дифференциальное уравнение:
По условию:
Окончательно получим:
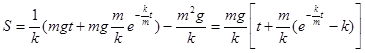
Дифференциальное уравнение не содержит явно независимой переменной, т. е. имеет вид
(2)
В этом случае понижение порядка достигается переходом к новому аргументу «у» и к новой функции 
. (
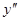пересчитаем так, чтобы получить производную по у).
Итак, положим 
. В таком случае 
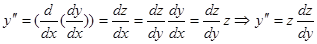(это преобразование как раз и позволило выразить 
через y и z).
Замечание. Необходимость такого преобразования вызывается тем, что после сделанного предположения, что у является независимой переменно, надо иметь в уравнении производную от функции z по у).
Теперь уравнение (2) преобразуется в уравнение первого порядка с неизвестной функцией z:
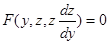
Решаем это уравнение (если возможно), получим общее решение в виде
Это уравнение с разделяющимися переменными
- общий интеграл данного дифференциального уравнения.
Пример. Найти частное решение уравнения 
, удовлетворяющее начальным условиям: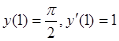 
Решение: Положим 
Используем начальные условия:
Частное решение:
Дифференциальное уравнение не содержит ни у, ни 
и может быть записано в виде
(3)
Это уравнение является простейшим типом уравнений, допускающих понижение порядка.
Здесь порядок понижается непосредственно путем последовательного интегрирования.
Из (3) сразу получаем:
Проинтегрировав таким образом дважды, получим общее решение уравнения (3).
Замечание. Несмотря на простоту этого типа уравнений, он играет важную роль, поэтому что к нему сводятся уравнения других видов, а также и потому, что к этому типу относятся некоторые уравнения, получающиеся при решении ряда задач сопротивления материалов, теоретической механики. (Пример – см. Гутер,, стр. 145)
Пример. Проинтегрировать дифференциальное уравнение
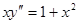
Решение.
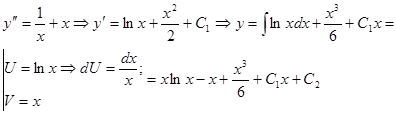
Уравнения, однородные относительно неизвестной функции и ее производных
Левая часть такого дифференциального уравнения 
- функция, однородная относительно 
, т.е. 
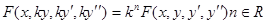(4).
Подстановкой 
мы понизим порядок уравнения на единицу. Доказано, тогда 
. Полагая 
(пользуясь тем, что параметр k можно выбрать произвольно) в равенстве (4), придем к соотношению:
И рассматриваемое уравнение может быть представлено в виде:
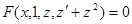
Если это уравнение удается проинтегрировать, то получим:
Пример. Решить однородное уравнение
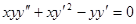
Решение. 
Сокращаем на 
.
Уравнение Бернулли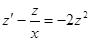 
Дифференциальное уравнение не содержит ни х, ни и может быть записано в виде
а) Так как в уравнении отсутствует х, то можно его решать приемом, указанным для случая 3.
б) Но можно дать и другой прием решения. Как известно,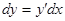 
. Умножим левую часть уравнения (5) на 
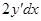, а правую - на 
:
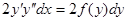
Левая часть представляет собой дифференциал от выражения 
, поэтому уравнение можно переписать следующим образом:
Задача. Определить скорость, с которой метеор ударяется о Землю, предполагая, что он падает прямолинейно с неограниченно большого расстояния из состояния покоя и при его движении к Земле ускорение обратно пропорционально квадрату его расстояния от центра Земли.
Решение. Обозначим расстояние метеора от центра Земли через r и составим дифференциальное уравнение:
Пришли к уравнению первого порядка.
Но r входит в уравнение, а r=r(t), поэтому сделаем такое преобразование:
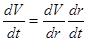Получим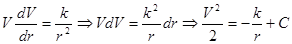 
Начальное условие: V=0 при 
Итак, 
Скорость при падении на Землю:
И т.д. (см. Гутер,, стр.139)
Задача. Найти закон движения материальной точки массы по прямой под действием отталкивающей силы, обратно пропорциональной третьей степени расстояния точки от неподвижного центра О.
O M x
S
Решение.
Пусть в момент времени t точка М находится на расстоянии S от точки О 
, с другой стороны, 
.Получим уравнение: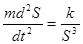 
(т.е. получим уравнение вида 
)
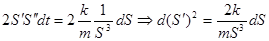т.е. умножим на 
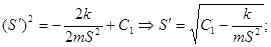знак «+» т.к. это скорость
или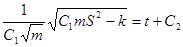 
Нужны дополнительные условия.
Замечание. Задача решения уравнений третьего, четвертого порядков и тем более уравнений еще более высоких порядков очень сложна. Для частных типов уравнений n-го порядка n>2 можно применять те приемы понижения порядка, которые только что рассмотрели, при тех же предположениях относительно вида уравнения.
Пример 1.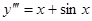 
Решение. 
Пример 2. 
Решение. Так как в уравнении отсутствует y, то положим 
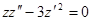- это уравнение второго порядка также допускает понижение порядка. Отсутствует независимая переменная, поэтому положим 
, т.е. будем считать z - аргумент.
(здесь взяли: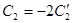 
)
