(1)
(его левая часть линейна относительно неизвестной функции y ее последовательных производных).
Коэффициенты 
и правая часть «b» - произвольные функции от х.
Обычно принято линейное уравнение писать в «приведенном виде», что достигается делением обеих частей уравнения на коэффициент 
получим уравнение следующего вида (при условии, что 
) (зависимость коэффициентов от х укажем явным образом):
Уравнение вида (2) называются линейным неоднородным уравнением, или уравнением с правой частью.
Если же 
, то уравнение принимает вид
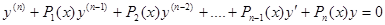
И его называют линейным однородным дифференциальным уравнением, или уравнением без правой части.
Для линейных дифференциальных уравнений теорему существования и единственности решения можно сформулировать так.
Теорема. Пусть коэффициенты 
линейного дифференциального уравнения (2) непрерывны на некотором отрезке [a,b]. Существует одно и только одно решение 
уравнения (2), определенное непрерывное на всем интервале ]a,b[, удовлетворяющее этому уравнению и любой системе начальных условий, если только значение 
]a,b[.
Доказательство этой теоремы опускаем.
Замечание. Условия существования и единственности решения выполняются для линейного уравнения не только в достаточно малой окрестности начальных условий (как это имеет место в общем случае), но на любом отрезке, на котором непрерывны функции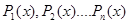 
(т.к. известно, что функции, непрерывна на замкнутом интервале, ограничены на нем). – см. Гутер,, стр. 157
Обозначим левую часть уравнения (3) через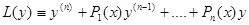 
.
Это выражение называется линейным дифференциальным оператором от функции у. Тогда линейное однородное уравнение (3) можно, воспользовавшись линейным оператором, записать в виде:
(3’)
Рассмотрим теоремы о свойствах частных решений линейного однородного дифференциального уравнения (3).
Теорема 1. Если функция 
является решением уравнения (3), то и функция 
, где C - произвольная постоянная, есть решение этого уравнения.
Доказательство. Так как - решение уравнения (3), то 
.
Вычислим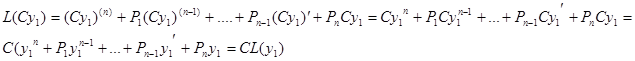 
Так как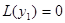 
. Это и означает, что функция 
также решение уравнения (3) (т.е. удовлетворяет уравнению (3))
Теорема 2. Если функции 
и 
являются решениями уравнения (3), то и функция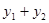 
есть решение этого уравнения.
Доказательство. Так как 
и – решения уравнения (3), то 
, 
С другой стороны, 
, т.е. функция 
, действительно, являются решением уравнения (3).
Замечание. Теорема верна и для нескольких слагаемых.
Теорема 3. Если 
- частные решения линейного однородного дифференциального уравнения (3), то их линейная комбинация 
(где 
- произвольные постоянные) есть также решение этого уравнения.
Эта теорема является очевидным следствием двух предыдущих.
Доказано, по теореме 1 слагаемые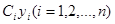 
- решения для (3), а тогда по теореме 2 и их сумма есть решение этого уравнения.
Линейная независимость функций.
Определитель Вронского.
Определение 1. Функции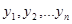 
, определенные на одном и том же отрезке [a,b], называется линейно зависимыми на [a,b], если существует n таких чисел 
, из которых хотя бы одно отлично от нуля, что выполняется тождественное соотношение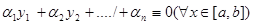 
(1).
Замечание. Предполагается, как видим, что числа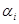 
не равны нулю одновременно.
Предположим, что 
, тогда тождество (1) можно переписать в виде
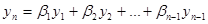(2)
где положено 
.
Поэтому линейная зависимость системы функций означает, хотя бы одна из функций системы представляет собой линейную комбинацию остальных.
Если же такие коэффициенты 
подобрать невозможно, т.е. никакая линейная комбинация функций 
не является тождественным нулем (разумеется, кроме случая, когда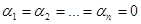 
), то такая система функций называется линейно независимой.
Рассмотрим несколько примеров:
1) Пусть 
Эти функции линейно зависимы на интервале 
.
Доказано, при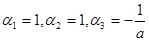 
имеем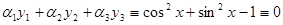 
.
2) 
- линейно независимы в : если при некоторых постоянных 
будем иметь: 
, то
при х=0, 
при х=1 из равенства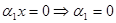 
Пример 2 (Уваров, стр. 447) 
- эти функции линейно независимы на 
. Пусть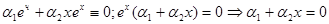 
В частности, при х=0 получаем из последнего равенства 
. А тогда из равенства 
при х=1, например.
См. Араман Линейная независимость.
Возникает необходимость в рассмотрении признаков, которые дали бы возможность установить линейную зависимость или независимость некоторой системы функций.
Пусть функции 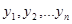имеют производные до (n-1)-го порядка включительно. Тогда из них можно построить определитель n-го порядка, который имеет вид:
Этот определитель также является функцией от x и обозначается
По имени польского математика И. Вронского, который впервые ввел его в рассмотрение, он назван определителем Вронского (или вронскианом) данной системы функций.
Вронскиан является средством изучения линейной зависимости или независимости системы функций. Его применение основано на следующих двух теоремах.
Теорема 1. Если функции 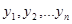линейно зависимы, то иx вронскиан тождественно равен нулю.
Доказательство. Для большей наглядности доказательство теоремы проведем для случая n=3. Пусть функции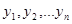 
- линейно зависимы. Тогда существуют коэффициенты 
(не равные одновременно нулю), для которых 
(3)
Предположим, что 
. В этом случае, разрешив равенство (3) относительно 
, получим: 
, где 
. Составим теперь для этих функций определитель Вронского и заменим в нем последний столбец, содержащий 
и ее производные:
Замечание. Можно было сразу к элементам третьего столбца прибавить элементы первого умноженные на 
и элементы второго, умноженные на 
.
Теорема 2. Если 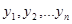- линейно независимые функции, удовлетворяющие некоторому линейному однородному дифференциальному уравнению n-го порядка, то их вронскиан не обращается в нуль ни водной точке.
Замечание. Функции рассматриваются при этом на некотором отрезке, лежащем строго внутри интервала ]a,b[, в котором можно гарантировать существование и единственность решения.
Таким образом, вронскиан функций 
определен на таком же отрезке, и теорема утверждает, что он на данном отрезке отличен от нуля.
Доказательство. Доказательство проведем методом «от противного»,ограничившись по прежнему случаем n=3.
Предположим, что 
хотя бы в одной точке 
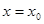. Покажем, что отсюда уже вытекает линейная зависимость функций 
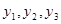, что противоречит предположению.
Итак, пусть существует точка 
, для которой 
. Тогда
Рассмотрим некоторую систему трех однородных уравнений с тремя неизвестными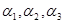 
коэффициентами которой служат строки определителя:
(4)
Определитель этой системы 
. Поэтому система (4) имеет ненулевое решение (если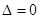 
для однородной системы, то она имеет ненулевое решение) т.е. хотя бы одно 
не равно нулю. С помощью этих чисел образуем новую функцию: 
(5), которая является линейной комбинацией функций 
(с коэффициентами, удовлетворяющими системе уравнений (4)).
Так как 
- решения некоторого линейного однородного дифференциального уравнения, то и функция 
также является решением этого уравнения (см. теорию в начале лекции).
Значит 
в силу первого из уравнений системы (4).
Аналогично,
Следовательно, функция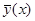 
в точке 
обращается в нуль вместе со своими производными, т.е. функция 
удовлетворяет не только дифференциальному уравнению, но также и нулевой системе начальных условий.
Дифференциальное уравнение однородное имеет и очевидное решение 
, удовлетворяющее той же нулевой системе начальных условий.
По теореме существования и единственности не может существовать двух различных решений дифференциального уравнения, удовлетворяющих одной и той же системе начальных условий.
Поэтому функция 
, где не все 
равны нулю. Последнее равенство означает линейную зависимость функций , что противоречит условиям теоремы. Следовательно, 
не обращается в нуль ни при каком значении х.
Определение. Систему частных решений линейного однородного дифференциального уравнения n-го порядка называют фундаментальной, если она состоит из n линейно независимых функций.
Структура общего решения линейного однородного дифференциального уравнения
Теорема. Если функции 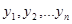образуют фундаментальную систему решений уравнения:
, то их линейная комбинация 
, где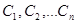 
- произвольные постоянные, является общим решением этого уравнения.
Доказательство. Для доказательства рассмотрим случай n=3. Тогда уравнение (1) будет иметь вид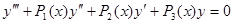 
.
Пусть - фундаментальная система решений уравнения (2). Составим линейную комбинацию 
, где 
- произвольные постоянные.
Так как - решения уравнения (2), то и функция (3) является решением этого уравнения. Остается показать, что функция (3) является общим решением уравнения (2).
Другими словами, достаточно показать, что любые начальные условия определяют решение, содержащиеся в формуле (3) (т.е. получающееся из этой формулы при надлежащем подборе постоянных 
).
Пусть задана некоторая система начальных условий:
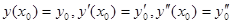
Подставим их в выражение (3):
Система (5) является неоднородной системой из трех алгебраических уравнений первой степени с тремя неизвестными 
. Ее определитель 
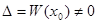, так как система 
фундаментальна, а значит, и линейно независима (по теореме второй вронскиан отличен от нуля в любой точке). Поэтому система (5) имеет единственное решение, т.е. можно подобрать произвольные постоянные 
так, чтобы функция (3) удовлетворяла начальным условиям (4).
Это означает, что функция (3) является общим решением уравнения (2).
Замечание. Приведенное доказательство может быть без изменения проведено и для любого n>3.
Вывод. Если система частных решений является фундаментальной, то общее решение уравнения (1) может быть сконструировано из частных, как их линейная комбинация с произвольными коэффициентами.
Тем самым задача интегрирования линейного однородного дифференциального уравнения сводится к задаче отыскания фундаментальной системы его частных решений. Последнюю не удается разрешить в общем виде.
Замечание. Смысл последней теоремы состоит еще и в том, что у линейного уравнения не может быть особых решения. (В уравнении (2) нет ни одного решения, не содержащегося в формуле (3)).
Пример. Показать, что функции 
и 
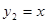образуют фундаментальную систему решений уравнения 
. Написать общее решение этого уравнения.
Решение. 1) Сначала покажем, что функции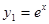 
и 
являются решениями данного уравнения:
2)Покажем, что функции 
и 
фундаментальную систему решений данного уравнения; т.е. что функции линейно независимы. Доказано, для этих функций вронскиан имеет вид: 
3) Общее решение уравнения имеет вид:
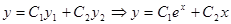
где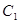 
и 
- произвольные постоянные.
Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Рассмотрим линейное однородное уравнение второго порядка:
В котором коэффициенты p и q являются постоянными.
В этом случае отыскание фундаментальной сиcтемы частных решений, а значит, и общего решения, сводится к чисто алгебраическим операциям – решению одного алгебраического уравнения второй степени (характеристического уравнения).
Левая часть этого уравнения представляет собой сумму самой функции y и ее производных 
, взятых с некоторыми постоянными коэффициентами. Чтобы такая сумма тождественно равнялась нулю, надо чтобы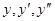 
были похожи, отличались друг от друга постоянными множителями.
Поэтому, например, ни одна из функций 
никак не может оказаться решением данного уравнения.
Вопрос к аудитории: «Не помните ли такую функцию, у которой производные похожи на саму функцию?»
Ответ: 
Итак, частные решения будем искать в виде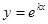 
.
Вид уравнения (1) показывает, что частные решения этого уравнения следует искать прежде всего среди таких функций, которые подобны своим производным (иначе при подстановке в левую часть (1) функции не произойдет взаимного уничтожения членов, ибо p и q теперь не функции).
Известно, что среди элементарных функций этим свойством обладает показательная функция. Поэтому будем искать частные решения в виде 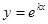, где k=const.
Так как 
, то для левой части уравнения (1) получаем: 
, yравнение приводится к виду: 
Множитель 
ни при каком значении x.Поэтому функция 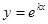тогда и только тогда удовлетворяет уравнению (1), когда число k является корнем уравнения
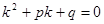
Уравнение (2) называется характеристическим уравнением данного дифференциального уравнения (1).
Оно получается из дифференциального уравнения (1) замещением в нем производных искомой функции соответствующей степенью неизвестного k, причем сама функция заменяется единицей.
Решение характеристического уравнения дает некоторую систему частных решений уравнения (1).
При решении характеристического уравнения могут представиться следующие случаи:
Корни характеристического уравнения действительные и различные (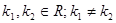
)
Пусть характеристическое уравнение имеет 2 различных действительных корня 
и 
.
Тогда частными решениями уравнения (1) будут функции 
и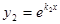 
.
Покажем, что они образуют фундаментальную систему, т.е. что они линейно независимы. Для этого составим определитель Вронского.
т.к. 
Следовательно, общее решение дифференциального уравнения (1) имеет вид:
Пример: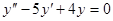 
Составим характеристическое уравнение: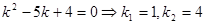 
Общее решение: 
Корни характеристического уравнения действительные и равные: 
Пусть , 
. Тогда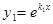 
является решением уравнения (1)
Нужно найти второе частное решение, линейно независимое с первым (функция 
тождественно равна функции и не может быть взята в качестве второго частного решения).
Положим 
, отсюда
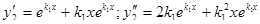
Подставим в левую часть уравнения (1):
Следовательно, функция является решением уравнения (1)
Покажем, что 
и 
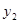образуют фундаментальную систему решения
Общее решение уравнения: 
Пример. 
Решение: 
Общее решение уравнения имеет вид 
Корни характеристического уравнения комплексные
Так как комплексные корни входят попарно сопряженными (трехчлен 
имеет действительные коэффициенты), то обозначим их так:
Им соответствует два частных решения
Выражение 
для общего решения неудобно, ибо содержит комплексные функции вида 
. Тогда как до сих пор мы ограничивались рассмотрением действительных функций действительного аргумента х.
Поэтому поставим своей целью получить общее решение таким, чтобы оно и в случае комплексных корней характеристического уравнения содержало бы лишь действительные функции.
Вместо решений 
рассмотрим некоторые их комбинации (которые также будут решениями уравнения (1) вследствие теорем 1 и 2 – см. начало предыдущей лекции).
Именно, рассмотрим функции
Применяя известные формулы Эйлера 
, преобразуем эти выражения следующим образом: 
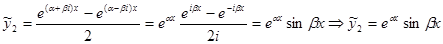
Итак, паре комплексных сопряженных корней характеристического уравнения можно поставить в соответствие пару действительных частных решений дифференциального уравнения.
Так как функции 
и 
образуют фундаментальную систему:
То общее решение уравнения:
Пример: 
Решение: 
.Общее решение данного уравнения имеет вид: 
Вывод: Таким образом, процесс решения линейного однородного уравнения с постоянными коэффициентами не содержит действия интегрирования, а состоит из простых алгебраических выкладок. В этом заключается большое преимущество линейных дифференциальных уравнений по сравнению с нелинейными.
Задача (Ноздрин И.Н., Степаненко И.М., Костюк Л.К., прикладные задачи по высшей математике, №507)
Длинный и тонкий призматический стержень сжимается продольно двумя, направленными по оси стержня, силами Р (см. рис.)
P y
x
l A
P
Определить критическое значение силы Р, при которой стержень начинает выпучиваться (задача Эйлера), если уравнение изогнутой оси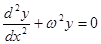 
, где 
; Е - модуль упругости, I - момент инерции поперечного сечения.
Решение: 
- общее решение уравнения.
Используем начальные условия: 
(это будет тривиальное решение) – прямолинейная форма равновесия.
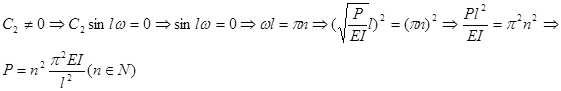
Наименьшая из этих сил P называется критической силой Эйлера, создающей изгиб стержня).
Линейные неоднородные дифференциальные уравнения
Неоднородным линейным дифференциальным уравнением называют уравнение вида
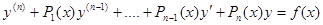(1)
Пользуясь выражением для линейного дифференциального оператора, можно записать уравнение (1) в виде:
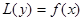(2)
Часто приходится наряду с уравнением (2) рассматривать однородное уравнение 
, получающееся из уравнения (2) отбрасыванием правой части. Такое однородное уравнение называют соответствующим данному неоднородному.
Структура общего решения линейного неоднородного дифференциального уравнения
Теорема. Общее решение линейного неоднородного дифференциального уравнения представляет сумму частного решения этого уравнения и общего решения соответствующего однородного.
Доказательство. Рассмотрим уравнение (2): 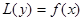. Обозначим через 
- известное частное решение этого уравнения, 
. Введем новую искомую функцию Y, связанную с y равенством:
Тогда уравнение (2) перейдет в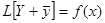 
, или (для простоты доказательства возьмем n=3)
т.е. функция оказывается удовлетворяющей соответствующему однородному уравнению, т.е. L(Y)=0. Если функции 
образуют фундаментальную систему частных решений, то 
Общее решение неоднородного уравнения получает вид: 
.
Доказательство этого:
Доказательство того, что выражение (3) представляет общее решение, проводится так же, как и доказательство теоремы об общем решении однородного уравнения.
Наличие изменяет только правые части системы для нахождения произвольных постоянных, что не отражается на ее разрешимости.
Доказано, пусть даны начальные условия:
Для того чтобы функция (3) удовлетворяла этим условиям, должно быть:
где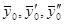 
- значения функции и ее производных в точке 
.
Перепишем эту систему в виде:
(4)
Определитель этой системы есть вронскиан 
, который отличен от нуля (как и для однородного уравнения) – так как система фундаментальна, а значит, и линейно независима.
Следовательно, система (4) совместна и имеет единственное решение, откуда вытекает, что функция (3) является общим решением рассматриваемого дифференциального уравнения.
Такое же рассуждение можно применить для уравнения любого порядка.
Вывод. Таким образом, для решения неоднородного линейного уравнения новым по сравнению с решением однородного уравнения является лишь отыскание какого-либо частного решения неоднородного уравнения.
На этом основан способ решения неоднородных уравнений.
Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Перейдем к рассмотрению способа неопределенных коэффициентов для нахождения частного решения неоднородного линейного уравнения.
Способ неопределенных коэффициентов применим для неоднородных уравнений с постоянными коэффициентами и со специальным видом правой части.
Рассмотрим линейное неоднородное дифференциальное уравнение второго порядка, в котором коэффициенты p и q - постоянные величины:
(1)
Нахождение общего решения соответствующего однородного уравнения мы рассматривали выше. Остается найти частное решение неоднородного уравнения.
Если правая часть содержит показательные функции (экспоненты), синусы, косинусы и многочлены или их целые рациональные комбинации (т.е. линейные комбинации указанных функций), то способ неопределенных коэффициентов позволяет подобрать частное решение неоднородного уравнения.
Способ неопределенных коэффициентов основан на знании формы частного решения. Естественно, что частное решение следует искать в форме, аналогичной форме правой части. Однако форма частного решения зависит также и от вида левой части уравнения.
Рассмотрим различные правые части в уравнении (1):
1. Правая часть уравнения (1) имеет вид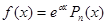 
(2)
где 
- многочлен степени n.
Таким образом будем рассматривать уравнение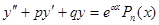 
, в котором коэффициенты p и q - постоянные.
Частное решение будем искать в форме 
, где Q(x) - многочлен, степень и коэффициенты которого надлежит подобрать.
Будет показано, что при надлежащем подборе степени этого многочлена нахождение решения в такой форме всегда возможно.
Результат подстановки функции в уравнение (2) даст следующее: для краткости Q(x) аргумент опускается.
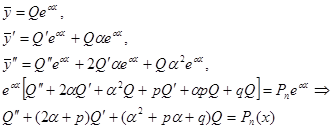
Для нахождения из равенства (3) неопределенных коэффициентов многочлена необходимо и достаточно, чтобы степени многочленов в левой и правой частях равенства (3) совпадали, т.е. чтобы степень левой части, так же как и правой, равнялась n.
Отсюда уже ясно, какова должна быть степень Q(x) в различных случаях. Возможны следующие частные случаи:
1. Число 
не является корнем характеристического уравнения, т.е.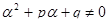 
. Для того чтобы равенство (3) обратилось в тождество, нужно взять в качестве Q(x) многочлен степени n (степень левой части в точности равна степени Q(x), так как производные от многочлена Q(x) имеют степень ниже, нежели степень Q(x) и для того чтобы иметь возможность найти неопределенные коэффициенты, многочлен Q(x) должен быть степени n.
Cтало быть, в том случае, когда правая часть имеет вид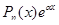 
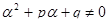и , частное решение следует искать в форме 
2. Пусть теперь число является однократным корнем характеристического уравнения (т.е. – корень характеристического уравнения первой кратности):
Левая часть равенства (3) будет начинаться с 
(левая часть не содержит Q(x). т.е. в левой части отсутствует член), поэтому степень многочлена Q(x) следует выбирать так, чтобы производная Q’(x) имела степень n. Сам многочлен Q(x) будет тогда иметь степень n+1.
Более того, равенство (3) позволяет определить только коэффициенты членов многочлена, содержащих x в соответствующей степени, свободный член в производные не входит, поэтому его можно полагать произвольным, в частности равным нулю.
Следовательно, 
.
3) число является двукратным корнем (т.е. корнем второй кратности) характеристического уравнения: 
Для того, чтобы равенство (3) обратилось в тождество, нужно взять в качестве Q(x) многочлен степени n+2 (в котором не надо брать свободного члена и члена с первой степенью x, т.к. эти члены не войдут в выражение второй производной); тогда 
Пример. Найти общее решение уравнения 
Решение. Соответствующее однородное уравнение
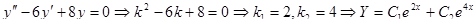
Следовательно, совпадает с корнем характеристического уравнения (т.е. 
– корень первой кратности характеристического уравнения); 
Следовательно, 
Общее решение уравнения: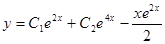 
Правая часть уравнения (1) имеет вид
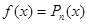
Многочлен можно рассматривать как частный случай выражения
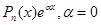
Пример. Найти общее решение уравнения
Решение: 
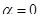- является корнем первой кратности характеристического уравнения
Подставим в уравнение: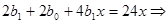 
Общее решение уравнения: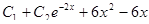 
Правая часть уравнения (1) имеет вид
Здесь комбинации выражени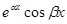й 
и 
можно рассматривать как комбинацию выражений, содержащих 
и 
(см. формулы Эйлера).
Аналогично рассмотренному выше можно установить, что в этом случае уравнению (1) будет удовлетворять функция, построенная по одному из следующих правил:
1) Если комплексные числа 
(где