Понятие перцептрона имеет интересную, но незавидную историю. В результате неразвитой терминологии нейронных сетей прошлых лет, резкой критики и непонимания задач исследования перцептронов, а иногда и ложного освещения прессой, изначальный смысл этого понятия исказился. Сравнивая разработки Розенблатта и современные обзоры и статьи, можно выделить 4 довольно обособленных класса перцептронов:
· Перцептрон с одним скрытым слоем - это классический перцептрон, которому посвящена бо́льшая часть книги Розенблатта, и рассматриваемый в данной статье: у него имеется по одному слою S-, A- и R-элементов.
· Однослойный перцептрон - это модель, в которой входные элементы напрямую соединены с выходными с помощью системы весов. Является простейшей сетью прямого распространения — линейным классификатором, и частным случаем классического перцептрона, в котором каждый S-элемент однозначно соответствует одному A-элементу, S—A связи имеют вес +1 и все A-элементы имеют порог 
= 1. Однослойные перцептроны фактически являются формальными нейронами, то есть пороговыми элементами Мак-Каллока — Питтса. Они имеют множество ограничений, в частности, они не могут идентифицировать ситуацию, когда на их входы поданы разные сигналы («задача XOR», см. ниже).
· Многослойный перцептрон (по Розенблатту) - это перцептрон, в котором присутствуют дополнительные слои A-элементов. Его анализ провёл Розенблатт в третьей части своей книги.
· Многослойный перцептрон (по Румельхарту) - это перцептрон, в котором присутствуют дополнительные слои A-элементов, причём, обучение такой сети проводится по методу обратного распространения ошибки, и обучаемыми являются все слои перцептрона (в том числе S—A). Является частным случаем многослойного перцептрона Розенблатта.
В настоящее время в литературе под термином «перцептрон» понимается чаще всего однослойный перцептрон (англ. Single-layer perceptron), причём, существует распространённое заблуждение, что именно этот простейший тип моделей предложил Розенблатт. В противоположность однослойному ставят «многослойный перцептрон» (англ. Multilayer perceptron), опять же, чаще всего подразумевая многослойный перцептрон Румельхарта, а не Розенблатта. Классический перцептрон в такой дихотомии относят к многослойным.
Обучение перцептронов
Важным свойством любой нейронной сети является способность к обучению. В своей книге Розенблатт пытался классифицировать различные алгоритмы обучения перцептрона, называя их системами подкрепления.
Система подкрепления - это любой набор правил, на основании которых можно изменять с течением времени матрицу взаимодействия (или состояние памяти) перцептрона.
Описывая эти системы подкрепления и уточняя возможные их виды, Розенблатт основывался на идеях Д. Хебба об обучении, предложенных им в 1949 году, которые можно перефразировать в следующее правило, состоящее из двух частей:
· Если два нейрона по обе стороны синапса (соединения) активизируются одновременно (то есть синхронно), то прочность этого соединения возрастает.
· Если два нейрона по обе стороны синапса активизируются асинхронно, то такой синапс ослабляется или вообще отмирает.
Обучение с пощрением
Классический метод обучения перцептрона — это метод коррекции ошибки. Он представляет собой такой вид обучения с поощрением, при котором вес связи не изменяется до тех пор, пока текущая реакция перцептрона остается правильной. При появлении неправильной реакции вес изменяется на единицу, а знак (+/-) определяется противоположным от знака ошибки.
Допустим, мы хотим обучить перцептрон разделять два класса объектов так, чтобы при предъявлении объектов первого класса выход перцептрона был положителен (+1), а при предъявлении объектов второго класса — отрицательным (−1). Для этого выполним следующий алгоритм:
1. Случайным образом выбираем пороги для A-элементов и устанавливаем связи S—A (далее они изменяться не будут).
2. Начальные коэффициенты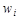 
полагаем равными нулю.
3. Предъявляем обучающую выборку: объекты (например, круги либо квадраты) с указанием класса, к которым они принадлежат.
◦ Показываем перцептрону объект первого класса. При этом некоторые A-элементы возбудятся. Коэффициенты 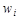, соответствующие этим возбуждённым элементам, увеличиваем на 1.
◦ Предъявляем объект второго класса и коэффициенты 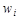тех A-элементов, которые возбудятся при этом показе, уменьшаем на 1.
4. Обе части шага 3 выполним для всей обучающей выборки. В результате обучения сформируются значения весов связей .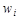
Теорема сходимости перцептрона, описанная и доказанная Ф. Розенблаттом (с участием Блока, Джозефа, Кестена и других исследователей, работавших вместе с ним), показывает, что элементарный перцептрон, обучаемый по такому алгоритму, независимо от начального состояния весовых коэффициентов и последовательности появления стимулов всегда приведет к достижению решения за конечный промежуток времени.
Обучение без поощрения
Кроме классического метода обучения перцептрона Розенблатт также ввёл понятие об обучении без поощрения, предложив следующий способ обучения:
Альфа-система подкрепления - это система подкрепления, при которой веса всех активных связей 
, которые ведут к элементу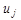 
, изменяются на одинаковую величину 
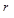, а веса неактивных связей за это время не изменяются.
Затем, с разработкой понятия многослойного перцептрона, альфа-система была модифицирована и её стали называть дельта-правило. Модификация была проведена с целью сделать функцию обучения дифференцируемой (например, сигмоидной), что в свою очередь нужно для применения метода градиентного спуска, благодаря которому возможно обучение более одного слоя.