Так как сети с обратными связями имеют пути, передающие сигналы от выходов к входам, то отклик таких сетей является динамическим, т. е. после приложения нового входа вычисляется выход и, передаваясь по сети обратной связи, модифицирует вход. Затем выход повторно вычисляется, и процесс повторяется снова и снова. Для устойчивой сети последовательные итерации приводят к все меньшим изменениям выхода, пока в конце концов выход не становится постоянным. Для некоторых сетей процесс никогда не заканчивается, такие сети называют неустойчивыми. Проблема устойчивости будет рассмотрена в следующем разделе, а здесь мы рассмотрим основной цикл работы сети.
Как только веса заданы, сеть может быть использована для получения запомненного выходного вектора по данному входному вектору, который может быть частично неправильным или неполным. Для этого выходам сети сначала придают значения этого начального вектора. Затем сеть последовательно меняет свои состояния согласно формуле:
| (9) |
где 
- функция активации, 
и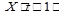 
- текущее и следующее состояния сети, до тех пор, пока состояния 
и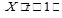 
не совпадут (или, в случае синхронного режима работы, не совпадут состояния 
с 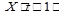и одновременно 
с X(t)). Именно этот процесс называется конвергенцией сети.
Это же можно описать так называемым локальным полем 
действующим на нейрон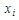 
со стороны всех остальных нейронов сети:
| (10) |
После расчета локального поля нейрона 
это значение используется для расчета значения выхода через функцию активации, которая в данном случае является пороговой (с нулевым порогом). Соответственно, значение выхода нейрона i в текущий момент времени 
рассчитывается по формуле:
|
|
| (11) |
, где 
- весовой коэффициента между нейронами i и j,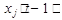 
- значения выходов нейрона j в предыдущий момент времени.
Во время работы сети Хопфилда признаком нахождения решения является момент, когда достигается аттрактор, статический (когда на каждом следующем шаге повторяется устойчивое состояние ) или, возможно, динамический (когда до бесконечности чередуются два разных состояния 
). Это конечное состояние сети и является ее реакцией на данный образ.
Обычно ответом является такое устойчивое состояние, которое совпадает с одним из запомненных при обучении векторов, однако при некоторых условиях (в частности, при слишком большом количестве запомненных образов) результатом работы может стать так называемый ложный аттрактор ("химера"), состоящий из нескольких частей разных запомненных образов, а также в синхронном режиме сеть может прийти к динамическому аттрактору. Обе эти ситуации в общем случае являются нежелательными, поскольку не соответствуют ни одному запомненному вектору - а соответственно, не определяют класс, к которому сеть отнесла входной образ.
Идея работы сети Хэмминга состоит в нахождении расстояния Хэмминга от тестируемого образа до всех образцов. Расстоянием Хэмминга называется число отличающихся битов в двух бинарных векторах. Сеть должна выбрать образец с минимальным расстоянием Хэмминга до неизвестного входного сигнала, в результате чего будет активизирован только один выход сети, соответствующий этому образцу.
Алгоритм функционирования сети Хэмминга следующий:
|
|
1. На входы сети подается неизвестный вектор 
, исходя из которого рассчитываются состояния нейронов первого слоя (верхний индекс в скобках указывает номер слоя):
| (12) |
После этого полученными значениями инициализируются значения аксонов второго слоя:
| (13) |
2. Вычислить новые состояния нейронов второго слоя:
| (14) |
и значения их аксонов:
| (15) |
Функция активации 
имеет вид порога, причем высота порога должна быть достаточно большой, чтобы любые возможные значения аргумента не приводили к насыщению.
3. Проверить, изменились ли выходы нейронов второго слоя за последнюю итерацию. Если да – перейди к шагу 2. Иначе – конец.
Для сети Хопфилда могут существовать две модификации отличающиеся по времени передачи сигнала: асинхронный и синхронный режимы.