ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА
ПОВЕРХНОСТНОГО НАТЯЖЕНИЯ ЖИДКОСТИ
ПО МАКСИМАЛЬНОМУ ДАВЛЕНИЮ В ПУЗЫРЬКЕ
Методические указания к выполнению
лабораторных работ по физике для студентов
всех специальностей всех форм обучения
Одобрено и рекомендовано к печати
научно-методическим семинаром
кафедры «Общая физика» СГТУ
Саратов 2011
Составители – Вахлюева Валентина Ивановна.
Боженькин Василий Михайлович.
Беляев Илья Викторович.
Рецензент – д.т.н., профессор кафедры ОФ Сысоев Виктор Владимирович
© Саратовский государственный
технический университет 2011 г.
Жидкость – агрегатное состояние вещества, промежуточное между газообразным и твердым, поэтому она обладает свойствами как газообразных так и твёрдых веществ. Жидкости, подобно твёрдым телам обладают большой объёмной упругостью, обладают определенным объёмом, сопротивляются изменению своего объёма, а подобно газам не обладают упругостью формы, принимают форму сосуда, в котором они находятся. В жидкостях имеет место так называемый ближний порядок в расположении частиц, то есть их упорядоченное расположение, повторяющееся на расстояниях, сравнимых с межатомными (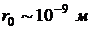 ). Молекулы в жидкости интенсивно взаимодействуют друг с другом. Силы их взаимодействия специфичны, то есть существенно зависят от природы взаимодействующих молекул и сильно различаются по величине для разных жидкостей.
). Молекулы в жидкости интенсивно взаимодействуют друг с другом. Силы их взаимодействия специфичны, то есть существенно зависят от природы взаимодействующих молекул и сильно различаются по величине для разных жидкостей.
При увеличении внешнего давления на величину 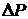 объём жидкости уменьшается на некоторую величину
объём жидкости уменьшается на некоторую величину 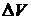 . При этом между сближающимися молекулами возникают огромные силы отталкивания, поэтому -
. При этом между сближающимися молекулами возникают огромные силы отталкивания, поэтому - 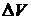 составляет лишь незначительную долю первоначального объёма –
составляет лишь незначительную долю первоначального объёма – 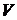 . Изотермическая сжимаемость жидкости
. Изотермическая сжимаемость жидкости 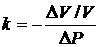 , то есть, при увеличении давления на 1 атм объём жидкости уменьшается на 10-4 ¸ 10-5 от своего первоначального значения. Сравнительно мало меняют свой объём жидкости и при нагревании. Термический коэффициент расширения жидкости
, то есть, при увеличении давления на 1 атм объём жидкости уменьшается на 10-4 ¸ 10-5 от своего первоначального значения. Сравнительно мало меняют свой объём жидкости и при нагревании. Термический коэффициент расширения жидкости 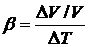 порядка 10-4 К-1.
порядка 10-4 К-1.
|
|
Поэтому в отличие от газов, работа изобарического расширения при нагревании жидкости на 1К относительно мала
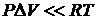 .
.
Величины 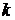 и
и 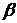 различны для разных жидкостей, непостоянны и являются сложными функциями давления и температуры. Для воды наблюдается аномалия: в интервале от 0 до 40С при нагревании происходит уменьшение объёма, то есть величина
различны для разных жидкостей, непостоянны и являются сложными функциями давления и температуры. Для воды наблюдается аномалия: в интервале от 0 до 40С при нагревании происходит уменьшение объёма, то есть величина 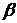 становится отрицательной.
становится отрицательной.
Характер теплового движения молекул в жидкости существенно отличается от теплового движения молекул газа. Поскольку средние расстояния 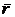 между молекулами в жидкости близки к
между молекулами в жидкости близки к 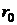 , отвечающему минимальному значению потенциальной энергии взаимодействия, то есть равновесию, то молекулы большую часть времени колеблются около своих положений равновесия. В силу хаотичности теплового движения скорости и амплитуды колебаний соседних молекул различны, и время от времени соседние молекулы расходятся друг от друга настолько, что отдельные молекулы перескакивают на расстояние порядка d, застревают в новых положениях равновесия, и начинают колебаться около них. С ростом температуры растёт средняя энергия теплового движения, а с ней и амплитуда колебаний и частота перескоков молекул из одного положения равновесия в соседние. При этом жидкость «разрыхляется», то есть при нагревании объём её возрастает.
, отвечающему минимальному значению потенциальной энергии взаимодействия, то есть равновесию, то молекулы большую часть времени колеблются около своих положений равновесия. В силу хаотичности теплового движения скорости и амплитуды колебаний соседних молекул различны, и время от времени соседние молекулы расходятся друг от друга настолько, что отдельные молекулы перескакивают на расстояние порядка d, застревают в новых положениях равновесия, и начинают колебаться около них. С ростом температуры растёт средняя энергия теплового движения, а с ней и амплитуда колебаний и частота перескоков молекул из одного положения равновесия в соседние. При этом жидкость «разрыхляется», то есть при нагревании объём её возрастает.
|
|
Поскольку в жидкости 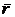 близко к
близко к 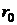 , то потенциальная энергия взаимодействия соседних молекул близка к величине
, то потенциальная энергия взаимодействия соседних молекул близка к величине  . При плотной упаковке молекул каждая из них окружена 12 ближайшими соседями, и её потенциальная энергия внутри жидкости приближенно равна
. При плотной упаковке молекул каждая из них окружена 12 ближайшими соседями, и её потенциальная энергия внутри жидкости приближенно равна 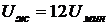 .
.
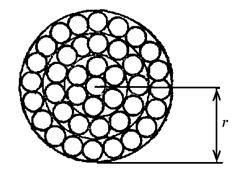 Молекулы взаимодействуют и на больших расстояниях, и, с ростом
Молекулы взаимодействуют и на больших расстояниях, и, с ростом 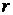 , энергия взаимодействия между двумя молекулами, как показывает детальное рассмотрение этой задачи, убывает как
, энергия взаимодействия между двумя молекулами, как показывает детальное рассмотрение этой задачи, убывает как 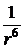 , то есть, если учесть все окружающие молекулы, энергия взаимодействия молекулы с окружающими будет уменьшатся быстрее, как
, то есть, если учесть все окружающие молекулы, энергия взаимодействия молекулы с окружающими будет уменьшатся быстрее, как 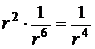 (так как в каждом последующем слое число молекул возрастает как
(так как в каждом последующем слое число молекул возрастает как 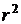 ). Поэтому полную энергию любой молекулы внутри жидкости можно практически считать не зависящей от объёма жидкости.
). Поэтому полную энергию любой молекулы внутри жидкости можно практически считать не зависящей от объёма жидкости.
Если слой жидкости тонкий, то энергия молекулы будет зависеть уже от его толщины и от растворенных в жидкости примесей. Если энергия взаимодействия молекулы растворенного вещества с молекулой растворителя 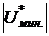 меньше энергии взаимодействия молекул растворителя
меньше энергии взаимодействия молекул растворителя 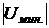 между собой, то при выходе растворенной молекулы на поверхность и вытеснении ею одной молекулы растворителя на поверхности в объём жидкости будет выделяться энергия
между собой, то при выходе растворенной молекулы на поверхность и вытеснении ею одной молекулы растворителя на поверхности в объём жидкости будет выделяться энергия 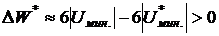 . Так как
. Так как 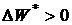 , то растворенные молекулы будут вытесняться на поверхность жидкости и одновременно будут понижать поверхностное натяжение раствора. Такие вещества носят название поверхностно - активных веществ.
, то растворенные молекулы будут вытесняться на поверхность жидкости и одновременно будут понижать поверхностное натяжение раствора. Такие вещества носят название поверхностно - активных веществ.
Расстояние r0, начиная с которого силами притяжения между молекулами можно пренебречь, называют радиусом молекулярного действия, а сфера радиуса r0 – сферой молекулярного действия.
|
|
Над поверхностью жидкости находится насыщенный пар. При не слишком высоких упругостях насыщенного пара расстояния между молекулами в паре велики по сравнению с их диаметрами, и потенциальная энергия молекул в паре практически равна нулю 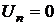 . Поскольку
. Поскольку 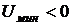 , то и
, то и 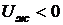 и, следовательно
и, следовательно 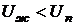 , то есть потенциальная энергия молекулы внутри жидкости меньше, чем потенциальная энергия той же молекулы в паре. При переходе молекулы из жидкости в пар необходима затрата работы по преодолению сил сцепления её с окружающими соседями
, то есть потенциальная энергия молекулы внутри жидкости меньше, чем потенциальная энергия той же молекулы в паре. При переходе молекулы из жидкости в пар необходима затрата работы по преодолению сил сцепления её с окружающими соседями

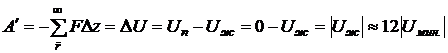
Следовательно, на испарение 1 моля, то есть N0 (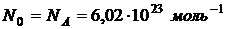 ,
, 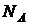 - число Авогадро) молекул жидкости, необходимо затратить работу
- число Авогадро) молекул жидкости, необходимо затратить работу
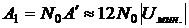
на преодоление внутренних сил сцепления между молекулами, то есть разрыв связей между ними.
Молярный объём жидкости 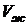 меньше, чем молярный объём пара
меньше, чем молярный объём пара 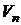 . При испарении происходит расширение вещества, что связано с добавочной работой расширения против сил внешнего давления
. При испарении происходит расширение вещества, что связано с добавочной работой расширения против сил внешнего давления
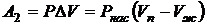 .
.
Тогда полная работа, производимая при испарении 1 моля жидкости, равна
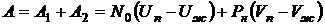 .
.
При испарении жидкости необходимую для этого энергию подводят в виде тепла. Температура при этом не меняется. Поэтому подводимое при испарении тепло называют скрытой теплотой испарения. При повышении температуры 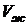 растёт,
растёт, 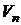 убывает, и свойства жидкости и её насыщенного пара сближаются. При критической температуре (см. реальные газы, уравнение Ван-дер-Ваальса)
убывает, и свойства жидкости и её насыщенного пара сближаются. При критической температуре (см. реальные газы, уравнение Ван-дер-Ваальса) 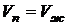 и, так как с увеличением плотности насыщенного пара расстояние между его молекулами уменьшается, потенциальная энергия
и, так как с увеличением плотности насыщенного пара расстояние между его молекулами уменьшается, потенциальная энергия 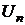 становится отличной от нуля и стремится к
становится отличной от нуля и стремится к 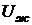 . При критической температуре
. При критической температуре 
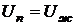 ;
; 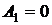 ;
; 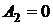 ;
; 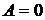 , исчезает различие между жидкостью и паром, скрытая теплота испарения обращается в нуль. Жидкость, налитая в сосуд, заполняет его и принимает форму сосуда. Сила тяжести прижимает жидкость ко дну сосуда, а свободная поверхность жидкости устанавливается горизонтально. Над поверхностью жидкости находятся насыщенный пар и газообразный воздух. Условия, в которых молекулы жидкости находятся на границах раздела, будут отличаться от условий внутри объёма жидкости. Молекулы, находящиеся в поверхностном слое жидкости, то есть на границе жидкость – газ, имеют в среднем только шесть ближайших соседей, а не 12. Поэтому её потенциальная энергия примерно равна
, исчезает различие между жидкостью и паром, скрытая теплота испарения обращается в нуль. Жидкость, налитая в сосуд, заполняет его и принимает форму сосуда. Сила тяжести прижимает жидкость ко дну сосуда, а свободная поверхность жидкости устанавливается горизонтально. Над поверхностью жидкости находятся насыщенный пар и газообразный воздух. Условия, в которых молекулы жидкости находятся на границах раздела, будут отличаться от условий внутри объёма жидкости. Молекулы, находящиеся в поверхностном слое жидкости, то есть на границе жидкость – газ, имеют в среднем только шесть ближайших соседей, а не 12. Поэтому её потенциальная энергия примерно равна 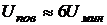 и больше, чем потенциальная энергия той же молекулы внутри жидкости,
и больше, чем потенциальная энергия той же молекулы внутри жидкости, 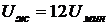 (так как
(так как 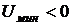 ). Поэтому для извлечения молекулы изнутри жидкости на её свободную поверхность надо затратить внешнюю работу
). Поэтому для извлечения молекулы изнутри жидкости на её свободную поверхность надо затратить внешнюю работу
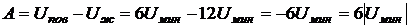 .
.
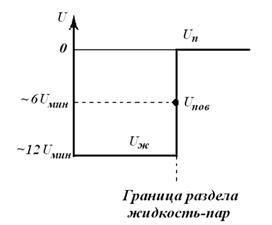 При обратном переходе молекулы из поверхностного слоя жидкости внутрь объёма её потенциальная энергия будет уменьшаться на ту же величину
При обратном переходе молекулы из поверхностного слоя жидкости внутрь объёма её потенциальная энергия будет уменьшаться на ту же величину 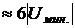 . Молекулы, находящиеся на свободной поверхности жидкости, будут стремиться, следовательно, перейти внутрь её объёма. Число молекул на поверхности жидкости пропорционально величине свободной поверхности. Поэтому стремление молекул втянуться внутрь объёма жидкости означает стремление сократить свободную поверхность жидкости и
. Молекулы, находящиеся на свободной поверхности жидкости, будут стремиться, следовательно, перейти внутрь её объёма. Число молекул на поверхности жидкости пропорционально величине свободной поверхности. Поэтому стремление молекул втянуться внутрь объёма жидкости означает стремление сократить свободную поверхность жидкости и 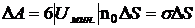 , где
, где 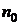 - число молекул на единице площади поверхности,
- число молекул на единице площади поверхности, 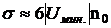 - коэффициент поверхностного натяжения, или просто поверхностное натяжение данной жидкости.
- коэффициент поверхностного натяжения, или просто поверхностное натяжение данной жидкости.
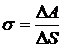 и
и 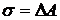 при
при 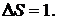
Коэффициент поверхностного натяжения 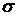 численно равен работе, которую надо затратить для увеличения поверхности жидкости на единицу площади
численно равен работе, которую надо затратить для увеличения поверхности жидкости на единицу площади 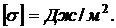
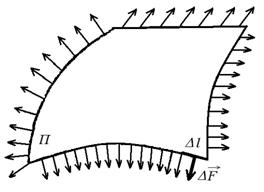 Выделим мысленно на поверхности жидкости площадку, ограниченную контуром П. Молекулы стремятся уйти внутрь жидкости с поверхности этой площадки, а площадка – сократиться. Плёнка находится в равновесии, а это значит, что на неё со стороны остальной поверхности действуют макроскопические растягивающие силы. То есть, к каждому элементу контура
Выделим мысленно на поверхности жидкости площадку, ограниченную контуром П. Молекулы стремятся уйти внутрь жидкости с поверхности этой площадки, а площадка – сократиться. Плёнка находится в равновесии, а это значит, что на неё со стороны остальной поверхности действуют макроскопические растягивающие силы. То есть, к каждому элементу контура 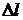 приложена сила поверхностного натяжения
приложена сила поверхностного натяжения 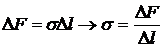 и
и 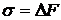 , если
, если 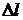 = 1. Коэффициент поверхностного натяжения численно равен силе поверхностного натяжения, действующей на единицу длины контура, ограничивающего поверхность
= 1. Коэффициент поверхностного натяжения численно равен силе поверхностного натяжения, действующей на единицу длины контура, ограничивающего поверхность 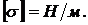
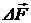 перпендикулярна к элементу контура
перпендикулярна к элементу контура 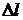 и лежит в плоскости, касательной к поверхности.
и лежит в плоскости, касательной к поверхности.
При переходе молекул с поверхности жидкости внутрь и обратно изменяется и кинетическая энергия их хаотического теплового движения. Следовательно, быстро сжимающаяся плёнка будет нагреваться, а быстро растягивающаяся плёнка – охлаждаться. Поэтому соотношение 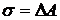 при
при 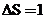 и
и 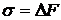 при
при 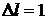 справедливы лишь при достаточно медленных изотермических процессах.
справедливы лишь при достаточно медленных изотермических процессах.
С ростом температуры взаимодействие молекул жидкости несколько ослабляется, так как при увеличении кинетической энергии молекул жидкость «разрыхляется» и среднее расстояние между молекулами увеличивается. Поэтому с увеличением температуры величина 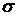 должна уменьшаться. Для большинства жидкостей поверхностное натяжение падает с температурой практически линейно по закону
должна уменьшаться. Для большинства жидкостей поверхностное натяжение падает с температурой практически линейно по закону 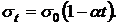
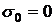 при
при 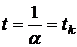 - критическая температура данной жидкости и
- критическая температура данной жидкости и
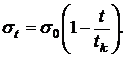
Если бы процесс увеличения площади протекал адиабатически, то совершенная над жидкостью работа была бы равна приращению внутренней энергии жидкости
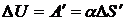 .
.
Но в этом случае приращение внутренней энергии слагалось бы не только из приращения поверхностной энергии 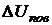 , но и из приращения объёмной энергии, то есть энергии внутренних частей жидкости
, но и из приращения объёмной энергии, то есть энергии внутренних частей жидкости 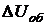 . Это вызвано тем, что увеличение поверхности сопровождается охлаждением жидкости (при переходе молекул из глубины жидкости в поверхностный слой скорость молекул уменьшается). Для того, чтобы внутренняя энергия изменялась только за счет поверхностной энергии (то есть чтобы (
. Это вызвано тем, что увеличение поверхности сопровождается охлаждением жидкости (при переходе молекул из глубины жидкости в поверхностный слой скорость молекул уменьшается). Для того, чтобы внутренняя энергия изменялась только за счет поверхностной энергии (то есть чтобы ( ), процесс увеличения поверхности жидкости нужно производить изотермически. В этом случае процесс увеличения поверхности за счет совершения работы
), процесс увеличения поверхности жидкости нужно производить изотермически. В этом случае процесс увеличения поверхности за счет совершения работы 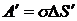 будет сопровождаться притоком из окружающей среды тепла
будет сопровождаться притоком из окружающей среды тепла 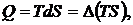 где
где 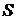 – энтропия поверхностного слоя жидкости (состояние и энтропия внутренних слоёв жидкости не изменяется). Таким образом, приращение внутренней энергии будет равно
– энтропия поверхностного слоя жидкости (состояние и энтропия внутренних слоёв жидкости не изменяется). Таким образом, приращение внутренней энергии будет равно
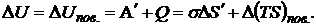
Это можно представить в виде:
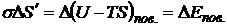
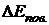 - свободная энергия поверхностного слоя жидкости.
- свободная энергия поверхностного слоя жидкости.
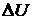 - внутренняя энергия, которой обладает поверхностный слой жидкости и которая при его сокращении может быть превращена в работу.
- внутренняя энергия, которой обладает поверхностный слой жидкости и которая при его сокращении может быть превращена в работу.
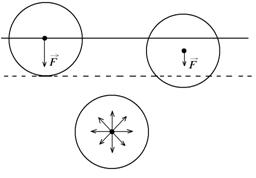
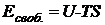
Для молекулы, находящейся на поверхности жидкости, молекулы нижней половины создают равнодействующую 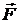 , которая не будет уравновешиваться силой взаимодействия молекул верхней половины сферы (взаимодействие со стороны молекул воздуха и паров ничтожно). Поэтому молекулы поверхностного слоя будут как бы втягиваться внутрь жидкости. То есть молекулы поверхностного слоя сжимают жидкость, производя на неё давление – молекулярное давление, тождественное с внутренним (молекулярным) давлением газа, выраженным членом
, которая не будет уравновешиваться силой взаимодействия молекул верхней половины сферы (взаимодействие со стороны молекул воздуха и паров ничтожно). Поэтому молекулы поверхностного слоя будут как бы втягиваться внутрь жидкости. То есть молекулы поверхностного слоя сжимают жидкость, производя на неё давление – молекулярное давление, тождественное с внутренним (молекулярным) давлением газа, выраженным членом 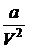 в формуле Ван-дер-Ваальса. Пользуясь этой формулой, можно вычислить молекулярное давление жидкостей. Оно оказывается равным тысячам атмосфер – этим и объясняется крайне малая сжимаемость жидкостей. Жидкость уже сжата большим молекулярным давлением и небольшое изменение внешнего давления вследствие этого мало влияет на изменение её объёма.
в формуле Ван-дер-Ваальса. Пользуясь этой формулой, можно вычислить молекулярное давление жидкостей. Оно оказывается равным тысячам атмосфер – этим и объясняется крайне малая сжимаемость жидкостей. Жидкость уже сжата большим молекулярным давлением и небольшое изменение внешнего давления вследствие этого мало влияет на изменение её объёма.
Таким образом, жидкость ведет себя так, как будто её поверхность представляет собой упругую пленку, стремящуюся сократится. Об этом говорит нам особое расположение молекул её поверхностного слоя, которые связаны между собой силами поверхностного натяжения. Об этом говорят и различные опыты. Направлена сила поверхностного натяжения по касательной к поверхности жидкости, перпендикулярно к участку контура, на который она действует.
Поверхностная плёнка жидкости по своим свойствам сходна с растянутой упругой плёнкой. Всякая изогнутая поверхностная пленка оказывает на жидкость добавочное давление по сравнению с тем, которое испытывает жидкость с плоской поверхностной пленкой: в случае выпуклой поверхности это добавочное давление положительно, в случае вогнутой – отрицательно.
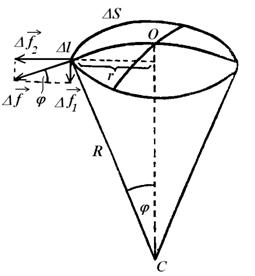
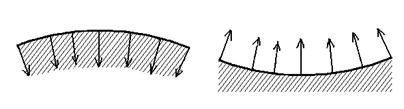
Определим добавочное давление над сферической поверхностью жидкости. Сферический сегмент 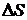 . Силы поверхностного натяжения, приложенные к контуру этого сегмента, повсюду касательны к сферической поверхности. На элемент
. Силы поверхностного натяжения, приложенные к контуру этого сегмента, повсюду касательны к сферической поверхности. На элемент 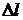 действует сила
действует сила 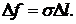 Эта сила составляет некоторый угол с радиусом
Эта сила составляет некоторый угол с радиусом 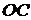 . Поэтому имеется отличная от нуля составляющая этой силы
. Поэтому имеется отличная от нуля составляющая этой силы  , направленная параллельно радиусу
, направленная параллельно радиусу 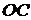 . Если поверхность выпукла, центр
. Если поверхность выпукла, центр 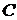 лежит внутри жидкости. В этом случае сила
лежит внутри жидкости. В этом случае сила 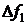 , сжимает жидкость, лежащую под сегментом
, сжимает жидкость, лежащую под сегментом 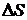 , то есть образует положительное давление; если поверхность вогнута, центр
, то есть образует положительное давление; если поверхность вогнута, центр 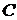 лежит вне жидкости. В этом случае
лежит вне жидкости. В этом случае  , растягивает жидкость, то есть оказывает отрицательное давление.
, растягивает жидкость, то есть оказывает отрицательное давление.
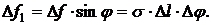
Такие силы 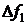 приложены ко всем элементам контура. Поэтому ко всему сферическому сегменту
приложены ко всем элементам контура. Поэтому ко всему сферическому сегменту 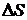 приложена параллельно радиусу
приложена параллельно радиусу 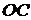 сила
сила
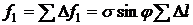
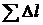 - длина контура, ограничивающего шаровой сегмент
- длина контура, ограничивающего шаровой сегмент 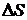 . Этот контур есть окружность радиуса
. Этот контур есть окружность радиуса 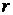 , то есть
, то есть 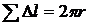 . Следовательно
. Следовательно
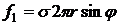
 ®
® 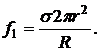
Давление 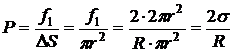 - добавочное давление, оказываемое на жидкость со стороны сферической поверхности.
- добавочное давление, оказываемое на жидкость со стороны сферической поверхности.
Наличие добавочного давления под изогнутой поверхностью ведет к тому, что внутри пузырька воздух находится под большим давлением, чем внешний воздух. Разность давлений воздуха внутри и вне пузыря тем больше, чем меньше радиус пузыря.
В случае произвольной искривленной поверхности, кривизна определяется соотношением 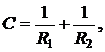
 где
где 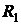 и
и 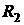 - радиусы кривизны двух взаимно перпендикулярных сечений. Кривизна
- радиусы кривизны двух взаимно перпендикулярных сечений. Кривизна 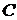 имеет одно и тоже значение для любой пары таких взаимно перпендикулярных нормальных сечений. Это средняя кривизна поверхности в точке
имеет одно и тоже значение для любой пары таких взаимно перпендикулярных нормальных сечений. Это средняя кривизна поверхности в точке 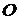 .
.
Рассуждая аналогично, как для сферы, получим
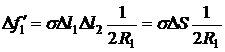
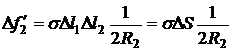 ,
,
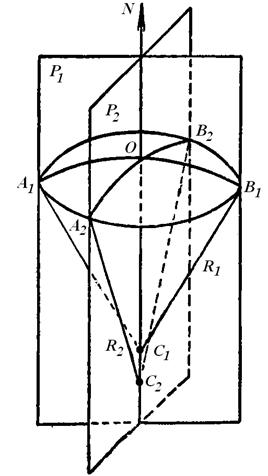
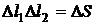 - площадь выделенного элемента. Выберем на кривой поверхности жидкости, имеющей произвольный вид, точку
- площадь выделенного элемента. Выберем на кривой поверхности жидкости, имеющей произвольный вид, точку 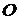 и проведем через эту точку два взаимно перпендикулярных сечения
и проведем через эту точку два взаимно перпендикулярных сечения 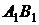 и
и 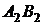 с радиусами кривизны
с радиусами кривизны 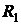 и
и 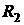 . Для определения давления, действующего на жидкость со стороны изогнутой поверхности, надо рассмотреть составляющую этой силы
. Для определения давления, действующего на жидкость со стороны изогнутой поверхности, надо рассмотреть составляющую этой силы 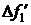 , направленной параллельно радиусу
, направленной параллельно радиусу 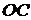 .
.
Поэтому 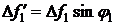 ,
, 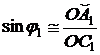 .
.
Дуга 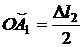 , а отрезок
, а отрезок 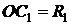 нормального сечения
нормального сечения 
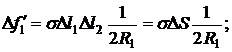
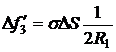 ;
; 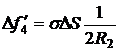
Соответственно, 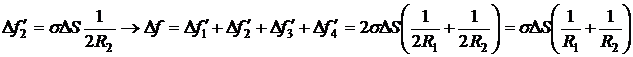
Давление 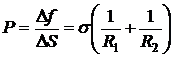 - формула Лапласа.
- формула Лапласа.
Дополнительное давление не зависит от r, то есть от того, в каком месте поверхности жидкости мы произвели мысленное сечение.
Плоскую поверхность жидкости можно рассматривать как предельный случай сферы бесконечно большого радиуса 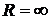 . В этом случае
. В этом случае 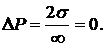
В случае плоской поверхности силы поверхностного натяжения направлены вдоль поверхности и не создают дополнительного давления; давление внутри жидкости равно внешнему давлению.
В случае шарообразного пузыря избыточное давление 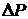 (по сравнению с атмосферным) внутри пузыря уравновешивается давлением со стороны стенок пузыря, обусловленным поверхностным натяжением. Если давление внутри пузыря увеличивается, то совершаемая при этом работа
(по сравнению с атмосферным) внутри пузыря уравновешивается давлением со стороны стенок пузыря, обусловленным поверхностным натяжением. Если давление внутри пузыря увеличивается, то совершаемая при этом работа 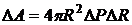 переходит в поверхностную энергию пузыря
переходит в поверхностную энергию пузыря 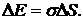
Согласно закону сохранения энергии,
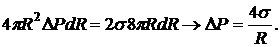
Так как это давление создается двумя изогнутыми поверхностями пузыря (внешней и внутренней), то давление, создаваемое одной поверхностью, в два раза меньше. (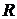 – радиус пузыря;
– радиус пузыря; 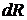 – увеличение радиуса при увеличении внутри него давления;
– увеличение радиуса при увеличении внутри него давления; 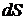 – суммарное увеличение внутренней и внешней поверхности пузыря:
– суммарное увеличение внутренней и внешней поверхности пузыря: 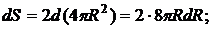
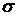 - поверхностное натяжение).
- поверхностное натяжение).
Если жидкость находится в сосуде, то, кроме свободной поверхности, существует граница раздела между жидкостью и твердым телом – стенками сосуда. Молекулы жидкости, соприкасающиеся со стенкой сосуда, взаимодействуют со своими ближайшими соседями как жидкости, так и твердого тела. Энергия такого взаимодействия приближённо равна
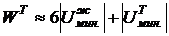 ,
,
где 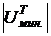 - энергия взаимодействия молекулы жидкости с молекулой твердого тела.
- энергия взаимодействия молекулы жидкости с молекулой твердого тела.
При переходе такой молекулы из пограничного слоя в объём жидкости будет выделяться энергия
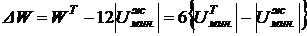 .
.
Если молекула жидкости сильнее взаимодействует с молекулами твердого тела, чем с молекулами той же жидкости, то 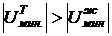 и
и 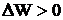 .
.
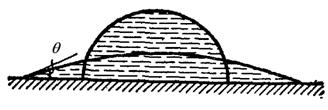
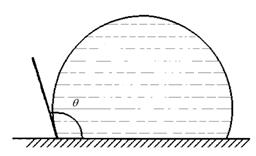
В этом случае жидкость будет стремиться увеличить поверхность соприкосновения с твердым телом и растечься по последнему. В этом случае принято говорить, что жидкость смачивает твердое тело (например, вода смачивает стекло). При таком растекании будет одно – временно возрастать и свободная поверхность капли, на что необходима затрата энергии. Процесс растекания жидкости прекратится, когда угол 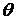 между свободной поверхностью жидкости и твёрдым телом сделается достаточно малым, достигнув некоторого предельного значения
между свободной поверхностью жидкости и твёрдым телом сделается достаточно малым, достигнув некоторого предельного значения 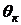 , характерного для данной пары жидкость – твердое тело, и называется краевым углом. Для жидкости, смачивающей данную поверхность, краевой угол
, характерного для данной пары жидкость – твердое тело, и называется краевым углом. Для жидкости, смачивающей данную поверхность, краевой угол 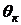 – острый (
– острый (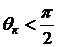 ) и тем меньше, чем лучше смачивание. Для очень хорошо смачивающей жидкости
) и тем меньше, чем лучше смачивание. Для очень хорошо смачивающей жидкости 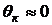 .
.
Если 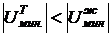 , то
, то 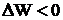 и жидкость будет стремиться сократить поверхность соприкосновения с твердым телом (ртуть – стекло). Жидкость несмачивающая. Краевой угол для несмачивающих жидкостей – тупой (
и жидкость будет стремиться сократить поверхность соприкосновения с твердым телом (ртуть – стекло). Жидкость несмачивающая. Краевой угол для несмачивающих жидкостей – тупой (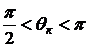 ).
).
 Форма, которую принимает свободная поверхность жидкости, зависит от сил поверхностного натяжения, от взаимодействия с ограничивающими поверхность твёрдыми стенками, а также от силы земного тяготения, действую- щей на жидкость. Особыми оказываются условия равновесия на линии раздела жидкость – газ – твердая стенка в тонких пленках и в узких сосудах - капиллярах. Такие явления называются капиллярными. Эти явления обусловлены тем, что благодаря действию сил поверхностного натяжения давление внутри жидкости может отличаться на некоторую величину
Форма, которую принимает свободная поверхность жидкости, зависит от сил поверхностного натяжения, от взаимодействия с ограничивающими поверхность твёрдыми стенками, а также от силы земного тяготения, действую- щей на жидкость. Особыми оказываются условия равновесия на линии раздела жидкость – газ – твердая стенка в тонких пленках и в узких сосудах - капиллярах. Такие явления называются капиллярными. Эти явления обусловлены тем, что благодаря действию сил поверхностного натяжения давление внутри жидкости может отличаться на некоторую величину 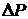 от внешнего давления
от внешнего давления 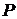 газа или пара над поверхностью жидкости.
газа или пара над поверхностью жидкости.
Если слой жидкости расположить между двумя близкими параллельными пластинками, поверхность жидкости примет форму круглого цилиндра радиуса 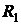 ,
, 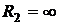 .
. 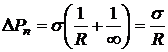 .
.
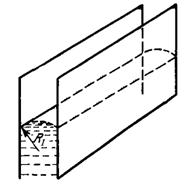
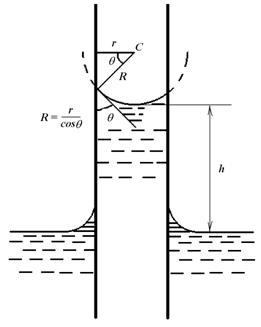
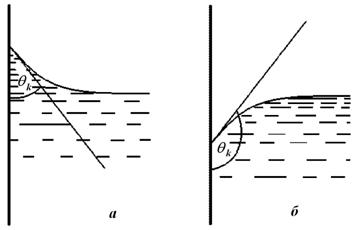
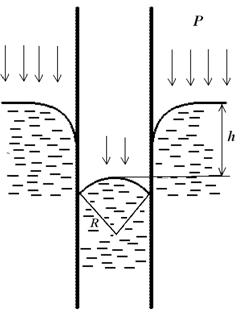 В узких трубках (капиллярах) вследствие смачивания или несмачивания жидкостью стенок капилляра кривизна поверхности жидкости (то есть мениск) становится значительной. Возникающее при этом дополнительное давление
В узких трубках (капиллярах) вследствие смачивания или несмачивания жидкостью стенок капилляра кривизна поверхности жидкости (то есть мениск) становится значительной. Возникающее при этом дополнительное давление 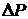 вызывает заметное поднятие или опускание уровня жидкости. Рассмотрим несмачивающую жидкость. Внутри капилляра образуется мениск и под действием дополнительного давления
вызывает заметное поднятие или опускание уровня жидкости. Рассмотрим несмачивающую жидкость. Внутри капилляра образуется мениск и под действием дополнительного давления 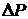 жидкость в капилляре опускается на некоторую глубину. В широком сосуде благодаря силе тяжести можно считать поверхность жидкости практически плоской. В узкой трубке можно пренебречь действием силы тяжести по сравнению с силами поверхностного натяжения и поверхность жидкости считать сферой некоторого радиуса
жидкость в капилляре опускается на некоторую глубину. В широком сосуде благодаря силе тяжести можно считать поверхность жидкости практически плоской. В узкой трубке можно пренебречь действием силы тяжести по сравнению с силами поверхностного натяжения и поверхность жидкости считать сферой некоторого радиуса 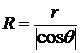 , где
, где 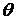 - краевой угол на границе жидкость – твердая стенка.
- краевой угол на границе жидкость – твердая стенка.
На уровне поверхности жидкости в капилляре давление в жидкости равно
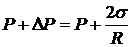 ,
,
где 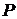 – внешнее давление в газе. По закону сообщающихся сосудов оно должно быть равно полному давлению на том же уровне в широком сосуде
– внешнее давление в газе. По закону сообщающихся сосудов оно должно быть равно полному давлению на том же уровне в широком сосуде 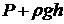 , где
, где 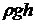 – гидростатическое давление столба жидкости плотности
– гидростатическое давление столба жидкости плотности 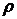 на глубине
на глубине 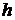 (
(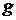 – ускорение силы тяжести). То есть,
– ускорение силы тяжести). То есть,
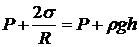 ®
® 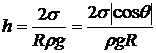 .
.
Точно такое же выражение получим и в случае поднятия жидкости в капилляре. При полном смачивании 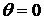 ,
, 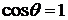 , радиус мениска
, радиус мениска 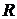 равен радиусу капилляра
равен радиусу капилляра 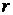 и высота поднятия жидкости
и высота поднятия жидкости 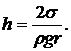
Цель работы: Определение коэффициента поверхностного натяжения жидкости по максимальному давлению в пузырьке.
Приборы и принадлежности: колбы с водой и исследуемой жидкостью, пипетка, пропущенная сквозь пробку, манометр, система, создающая разрежение в колбе, воронка.
Если опустить тонкий капилляр в жидкость и создать в капилляре давление большее, чем над поверхностью жидкости, то из капилляра в жидкость будут пробулькивать пузырьки. Вследствие явления поверхностного натяжения пузырек сжимается добавочным давлением, возникающим на его внутренней поверхности. Это давление зависит от радиуса пузырька 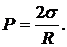
Радиус пузырька изменяется в процессе его образования и отрыва от капилляра. Сначала радиус пузырька велик, а добавочное давление мало. По мере продавливания пузырька, радиус его уменьшается. При этом возрастает сдерживающее его добавочное давление (оно обратно пропорционально радиусу).
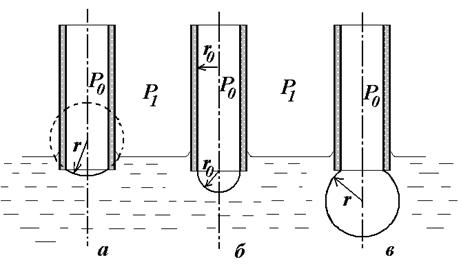
Так продолжается до тех пор, пока радиус пузырька 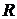 не станет равным радиусу капилляра
не станет равным радиусу капилляра 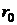 . При дальнейшем продавливании пузырька он теряет устойчивость. Радиус его снова увеличивается, добавочное давление уменьшается, что вызывает его дальнейшее расширение. Расширение идет лавинообразно, пузырек пробулькивает в жидкость и процесс повторяется.
. При дальнейшем продавливании пузырька он теряет устойчивость. Радиус его снова увеличивается, добавочное давление уменьшается, что вызывает его дальнейшее расширение. Расширение идет лавинообразно, пузырек пробулькивает в жидкость и процесс повторяется.
В момент перед пробулькиванием, сдерживающее давление 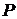 достигает максимума, а радиус принимает значение
достигает максимума, а радиус принимает значение 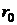 . Формула добавочного давления примет вид
. Формула добавочного давления примет вид 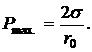
Определить 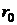 трудно, так как конец капилляра имеет обычно не слишком правильную форму. Поэтому используют относительный метод измерения.
трудно, так как конец капилляра имеет обычно не слишком правильную форму. Поэтому используют относительный метод измерения.
Сначала погружают капилляр в дистиллированную воду, для которой коэффициент поверхностного натяжения 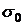 известен. Измеряют добавочное давление
известен. Измеряют добавочное давление  в момент перед пробулькиванием пузырька. Затем тот же капилляр погружают в исследуемую жидкость и измеряют добавочное давление
в момент перед пробулькиванием пузырька. Затем тот же капилляр погружают в исследуемую жидкость и измеряют добавочное давление 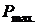 жидкости.
жидкости.
Для воды
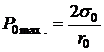 .
.
Для исследуемой жидкости
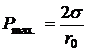 .
.
Радиус пузырька в момент отрыва один и тот же и равен радиусу капилляра 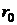 .
.
Взяв отношение последних равенств и решив его относительно 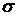 , получим
, получим
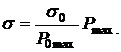
Полученная формула является рабочей формулой для определения 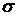 .
.
Измерения
Схема установки
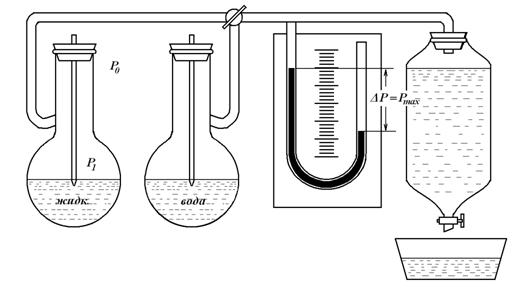
Трубочка с оттянутым капилляром (пипетка) пропущена сквозь пробку, плотно закрывающую колбу с исследуемой жидкостью, и погружена в жидкость на незначительную глубину.
Колба соединена с системой, в которой создается разряжение. При вытекании воды из сосуда, давление в системе 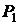 становится ниже атмосферного давления
становится ниже атмосферного давления 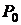 . Давление в пипетке остается атмосферным, так как она открыта сверху. Под действием разности давлений
. Давление в пипетке остается атмосферным, так как она открыта сверху. Под действием разности давлений 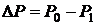 в жидкость из капилляра пробулькивают пузырьки.
в жидкость из капилляра пробулькивают пузырьки.
Разность давлений 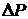 (в относительных единицах) измеряют манометром, одно колено которого соединено с системой, а другое – с атмосферой.
(в относительных единицах) измеряют манометром, одно колено которого соединено с системой, а другое – с атмосферой.
Легко видеть, что манометр измеряет добавочное давление в пузырьке. На воздушный пузырёк изнутри действует атмосферное давление 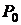 , передаваемое через капилляр, а снаружи – давление в системе
, передаваемое через капилляр, а снаружи – давление в системе 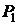 , передаваемое через жидкость, и добавочное давление
, передаваемое через жидкость, и добавочное давление 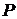 , созданное поверхностным натяжением жидкости. Гидростатическим давлением пренебрегаем, так как капилляр погружен на небольшую глубину.
, созданное поверхностным натяжением жидкости. Гидростатическим давлением пренебрегаем, так как капилляр погружен на небольшую глубину.
До отрыва пузырька давления снаружи и внутри практически уравновешиваются, так что 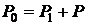 . Отсюда следует, что
. Отсюда следует, что 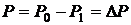 , то есть разность давлений равна добавочному давлению.
, то есть разность давлений равна добавочному давлению.
Измерения сводятся к определению максимального добавочного давления 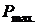 для исследуемой жидкости и
для исследуемой жидкости и  для воды.
для воды.
Порядок измерений следующий.
1. Погружают пипетку в колбу с водой, плотно вставив пробку. Чтобы воздух не проходил в систему вторую колбу перекрывают.
2. Слегка открывают кран, чтобы из него медленно по каплям вытекала вода в подставленный сосуд. Если пузырьки пробулькивают очень быстро, нужно замедлить течение воды.
3. Наблюдают за манометром. Перед пробулькиванием пузырька разность уровней в коленях манометра будет максимальной. Так как за уровнями трудно следить одновременно, то при пробулькивании одного пузырька берут отсчет по максимуму высоты в одном колене, где уровень выше, при пробулькивании следующего – отсчет по минимуму в другом колене. При пробулькивании следующих пузырьков отсчеты повторяют в том же порядке. Результаты немедленно записывают в таблицу. Измерения проводить не менее пятираз.
Таблица 1
| № опыта | Температура в лаборатории | Уровень в левом колене | Уровень в правом колене | 
| 
| 
|
| … | ||||||
| n |
Добавочное давление  равно разности отсчетов, а если шкала манометра имеет нуль посередине, то сумме отсчетов. Отсчеты по манометру производят с точностью до 1 мм.
равно разности отсчетов, а если шкала манометра имеет нуль посередине, то сумме отсчетов. Отсчеты по манометру производят с точностью до 1 мм.
4. Переключаем кран на колбу с исследуемой жидкостью и производим те же измерения, что и с водой. Заполняем аналогичную таблицу и определяем пять значений 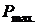 для жидкости.
для жидкости.
5. Получаем пятьзначений 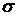 , подставив измеренные добавочные давления в рабочую формулу. Поверхностное натяжение воды
, подставив измеренные добавочные давления в рабочую формулу. Поверхностное натяжение воды 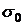 находим из таблицы 2, предварительно определив температуру в лаборатории.
находим из таблицы 2, предварительно определив температуру в лаборатории.
Таблица 2
Температура, 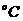
| ||||||
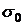 10 10 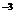 Н/м Н/м
| 74,22 | 73,49 | 73,05 | 72,75 | 71,97 | 71,18 |
Для промежуточных значений температуры вычисляют 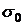 методом линейной интерполяции. Например, для
методом линейной интерполяции. Например, для 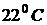
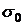 будет вычисляться следующим образом. При изменении температуры н
будет вычисляться следующим образом. При изменении температуры н