Расчет на прочность стальных зубчатых передач

 

5.1.1 Проверочный расчет цилиндрической прямозубой передачи.

Цилиндрические колёса, входящие в состав данной коробки скоростей имеют окружную скорость меньше 16 м/с, следовательно, целесообразно применять прямозубые передачи, а для конической передачи используем косозубые колёса. Расчет модуля таких передач поводится по изгибным () и контактным () напряжениям, а затем большее значение приводится к стандартному.

Для прямозубой цилиндрической передачи:

Исходные данные:

· количество зубьев шестерни составляет z=56,

· передаточное отношение равно i=1,

Расчетные формулы для стальных закаленных цилиндрических прямозубых зубчатых передач коробок скоростей и подач имеют вид:

 

, мм.

, мм.

 

где - крутящий момент на валу шестерни (меньшего колеса) передачи в Нм;

z - число зубьев шестерни;

i - передаточное число, равное отношению числа зубьев большего колеса к числу зубьев меньшего колеса (), независимо от того, понижающей передача или повышающая;

- знак плюс для подач наружного зацепления, минус внутреннего;

- коэффициент формы зуба, 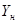=0,495;

 

 

b - рабочая ширина зубчатого венца колеса в мм; 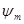=7;

 

- коэффициенты, учитывающие увеличение нагрузки на передачу по сравнению с номинальной вследствие неравномерного характера процесса резания в работы привода;

 

 

где 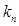‑ коэффициент перегрузки.

, ‑ коэффициенты динамичности нагрузки, учитывающие дополнительные динамические нагрузки на зубья колес, возникающие при работе передачи вследствие погрешностей ее изготовления и монтажа, а также деформаций зубьев под нагрузкой; ведя окружная скорость передачи

 

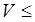1 м/с, то = =1;

 

коэффициенты неравномерности распределения нагрузки по длине зуба; учитывают увеличение нагрузки на опасном участке контактной линии вследствие упругих деформации валов и подшипников и погрешностей изготовления сопряженных колес, ведущих к взаимному перекосу контактирующих зубьев;

- допускаемое напряжение на изгиб и контактную прочность а определяются по формулам:

 

 

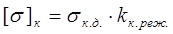
‑ длительные пределы выносливости зубьев при расчете на изгиб и контактную прочность в ;

‑ коэффициент, учитывающий влияние режима шлифования зубьев на величину допускаемого изгибного напряжения;

‑ коэффициенты переменности режима работы, учитывающие благоприятное влияние переменного режима работы универсального станка на величину допускаемого напряжения, когда через рассчитываемую передачу не всегда передается полная мощность, что позволяет повысить допускаемые напряжения по сравнению с длительными пределами выносливости; величина 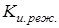берется из табл., а 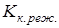рассчитывается по формуле:

 

 

где - расчетное (базовое) число циклов нагружения при испытании материала шестерни на усталостную прочность;

- количество передач в группе, где находится рассматриваемая передача;

- расчетная частота вращения шестерни в мин^-1;

‑ коэффициенты увеличения и , зависящие от степени универсальности станка в расположения передачи ближе к входному или выходному валу привода;

Определяем значения, необходимые для нахождения .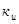

Учитывая отсутствие упругих и деформирующих элементов упругих муфт, резкий пуск и торможение и неравномерный характер процесса резания принимаем =1,4.

Предварительно принимаем модуль m=3

Определяем величину окружной скорости:

 

,м/с

 

Определяем отношение по формуле:

 

 

Принимаем 7-й класс точности, тогда =1,05

Определяем величину отношения:

 

 

Учитывая, что шестерня расположена вблизи одной опоры и вал жесткий принимаем =1,15.

Определяем значение коэффициента :

 

В качестве материала зубчатого колеса примем сталь 40Х. Вид термообработки – объемная закалка.

Для расчета допускаемого напряжения определим следующие параметры:

· предел выносливости принимаем =1,9*10⁸Н/м,

· коэффициент шлифования зуба принимаем =1,

· коэффициент универсальности станка принимаем для передачи расположенной ближе к входному валу =1,4

Определяем допускаемое изгибное напряжение:

 

Н/м²

 

Рассчитываем модуль зубчатой передачи по изгибным напряжениям:

 

 

Для расчета модуля по контактным напряжениям определяем: коэффициент увеличения нагрузки, для этого находим значения его составляющих.

Учитывая отсутствие упругих и деформирующих элементов упругих муфт, резкий пуск и торможение и неравномерный характер процесса резания принимаем =1,4.

По сделанным ранее расчетам принимаем =1,03.

Аналогично принимаем =1,1.

Определяем значение коэффициента :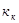

 

Для расчета допускаемого напряжения определим следующие параметры:

· предел выносливости принимаем =9,5*10⁸ ,

· коэффициент универсальности станка рассчитываем, для этого принимаем:

количество передач р=2,

базовое число циклов =7*10⁷,

 

=1,2;

=1,7.

 

Рассчитываем:

 

 

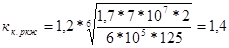
Определяем допускаемые контактные напряжения:

 

Н/м²

 

Рассчитываем модуль зубчатой передачи по изгибным напряжениям:

 

 

Принимаем ближайший стандартный модуль m=3

5.1.2 Проверочный расчет косозубой конической передачи

Исходные данные:

 

· количество зубьев шестерни составляет z=35,

· передаточное отношение равно i=1,

· угол наклона зуба - β = 25°,

· материал колеса - сталь 40Х, ТО – объёмная закалка.

 

Расчетные формулы для стальных закаленных цилиндрических прямозубых зубчатых передач коробок скоростей и подач имеют вид:

 

 

где - крутящий момент на валу шестерни (меньшего колеса) передачи в Нм;

z - число зубьев шестерни;

i - передаточное число, равное отношению числа зубьев большего колеса к числу зубьев меньшего колеса (), независимо от того, понижающей передача или повышающая;

- коэффициент, учитывающий форму зуба и концентрацию напряжений, выбирают в зависимости от эквивалентного числа зубьев z_v.

 

Z_v= .

 

В зависимости от Z_v выбираю у_F=3,815;

Коэффициент нагрузки предварительно принимаю K =1,5;

Коэффициент ширины колеса =7;

Определяем допускаемое изгибное напряжение:

 

Н/м²;

 

- коэффициент, учитывающий изменение нагрузочной способности по изгибающим напряжениям конической передачи по сравнению с цилиндрической прямозубой, =0,65+0,11i=0,65+0,11=0,76 (при твердости HRC > 45).

Тогда

 

 

Определяем внешний круговой модуль через средний модуль :

 

мм

 

Округляем полученное значение до стандартного, тогда =4,5 мм.

Определяем внешнее конусное расстояние:

 

мм, тогда фактический средний модуль равен:

 

 

где ,

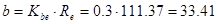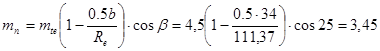мм, округляем до числа из стандартного ряда, и тогда мм;

 

мм.

 

Определенное значение внешнего конусного расстояния сравниваем с подсчитанным по формуле, так как имеем косозубую передачу:

 

= ≈77,2 мм

 

где - сумма зубьев колес пары;

111,37>77,2 - условие выполняется.

 

5.1.3 Проверочный расчет передач

Проверочный расчет конической передачи

Исходные данные:

 

m_te1,2 = 2,5, z_1,2 = 35, 7-A, δ = 45°; β = 25°, сталь 40Х, ТО - закалка ТВЧ.

 

Проверочный расчет на изгибную прочность

 

,

где 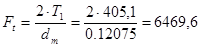Н,

d_m=m_mn*z=3,45*35=120,75мм,

K_F= K_Fβ· K_FV=1·1,4=1,4,

K_H= K_Hβ· K_HV=1,05·1,2=1,26,

K_Fβ=1+(K_Hβ - 1)·1.5=1+(1-1)·1.5=1,

Z_v= .

 

В зависимости от Z_v выбираю у_F=3,815. Тогда

 

МПа<[ ]=2,66·10⁸МПа –

 

Условие изгибной прочности выполняется.

Проверочный расчет на контактные напряжения

 

МПа<[ ],

[ ]=13,3·10⁸МПа

 

Условие контактной прочности выполняется.

Прочностной расчет конической передачи проведен успешно.

Проверочный расчет цилиндрической передачи.

Исходные данные:

 

m_1,2 = 3, z_1,2 = 56, 7-A, сталь 40Х, ТО - закалка ТВЧ.

 

Проверочный расчет на изгибную прочность

 

,

где ,Н,

где K – коэффициент нагрузки,

 

K= K_β · K_V · K_α

 

K_β – коэффициент неравномерности распределения нагрузки по длине зуба, K_β = 1,3;

K_V – коэффициент динамичности нагрузки, K_V=1,22;

K_α – коэффициент, учитывающий неравномерность распределения нагрузки между зубьями цилиндрических колес:

 

K_α = 1+0,06(П_ст-5),

 

где П_ст – назначенная степень точности передачи, П_ст=7

 

K_α = 1+0,06(7-5) = 1,12;

d=m*z=3*56=168 мм,

K= K_β · K_V · K_α= 1,3·1,22·1,12=1,78

Н.

 

В зависимости от Z_v выбираю у_F=3,825. Тогда:

 

МПа<[ ]=2,66·10⁸МПа –

 

Условие изгибной прочности выполняется.

Проверочный расчет на контактные напряжения

 

МПа<[ ], [ ]=13,3·10⁸МПа

Условие контактной прочности выполняется.

Прочностной расчет цилиндрической передачи проведен успешно.

 

5.2 Расчет зубчатой ременной передачи

 

Передача зубчатым ремнем по сравнению с клиновым или плоским ремнем при одинаковых габаритах позволяет передавать большой крутящий момент. Благодаря отсутствию скольжения она может быть использована для синхронизации вращения рабочих органов станка, манипулятора или промышленного робота. Передачу можно использовать при малых межцентровых расстояниях, повышенном значении передаточного числа. Допускается работа передачи в масле. В то же время для передачи зубчатым ремнем характерны повышенный шум при частоте вращения шкивов более 1500 об/мин, большая масса зубчатого ремня, относительно сложная конструкция шкивов.

Нагрузка на ремень. Исходные данные: номинальная мощность передаваемая ремнем Р=5,5 кВт, частота вращения шкива n=1600 об/мин, передаточное отношение передачи i=1.

Предварительно выбираю модуль передачи:

 

мм

 

Принимая модуль стандартным 5 мм, определяю наименьшее допускаемое число зубьев меньшего шкива , вычисляю диаметр его делительной окружности 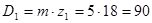мм и окружную скорость ремня:

 

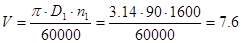м/с

Допускаемая удельная окружная сила, передаваемая ремнем , для модуля 5 мм равна 35Н/см.

Удельная расчетная сила, передаваемая ремнем, при которой долговечность передачи составляет 4000-7000ч,

 

 

- коэффициент, учитывающий передаточное число передачи, = 2;

- коэффициент, учитывающий число зубьев на дуге обхвата меньшева шкива, = 0,9;

- коэффициент, учитывающий наличие в передаче натяжного ролика, 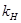= 1;

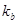- коэффициент, учитывающий неравномерность распределения нагрузки между витками каната в зависимости от ширины ремня, = 1;

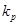- коэффициент, учитывающий влияние режима и длительности работы передачи, = 0,59;

- коэффициент, учитывающий влияние окружной скорости ремня на его долговечность, снижение работоспособности зубьев ремня из-за повышения частоты их нагружения и износа, = 1;

- коэффициент, учитывающий влияние длины ремня или межосевого расстояния а на его долговечность, а именно, повышение частоты нагружения зубьев ремней меньшей длины, их нагрев, неравномерность нагрузки по длине зубьев, =1;

 

Н/см.

 

Расчетная окружная сила, передаваемая ремнем:

Н

 

Расчетная ширина ремня:

 

мм

 

Принимаю ширину ремня стандартной 25мм.

Число зубьев и диаметр делительной окружности шкива:

 

мм;

 

Длина ремня без учета его провисания:

 

мм.

 

Ближайший по длине ремень выбирают по стандарту и вычисляют уточненное межосевое расстояние:

 

.

 

Проверка ремня по давлению на его зубьях

Расчетное давление на зубьях ремня:

 

,

где - коэффициент, учитывающий неравномерность распределения окружной силы между зубьями ремня по дуге охвата, = 2;

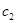- коэффициент, учитывающий неравномерность распределения давления по высоте зубьев ремня, 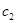=1,5;

- коэффициент, учитывающий неравномерность распределения давления по длине зубьев ремня, =1;

и ширина и высота ремня соответственно, мм.

 

, что позволяет использовать данный ремень, так как , при .

 

Параметры шкива

 

Для передачи с зубчатым ремнем шкивы принимают следующими:

Модуль передачи:

 

мм;

 

Диаметр окружности выступов:

 

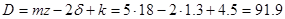мм;

 

Высота зуба мм;

Угол впадины

Окружной шаг по средней линии зубьев:

мм;

 

Толщина зуба:

 

мм;

 

Длина зуба:

 

мм;

 

Радиус головки зуба:

 

мм;

 

Радиус ножки зуба:

 

мм.