Скалярное, векторное, смешанное произведение.
Скалярное произведение 
хорошо известно из школьного курса.
Если 
то получаем 
.
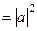Скалярное произведение обладает хорошо известным свойством:
.
Чтобы его запомнить, рассмотрим идею доказательства. Расположим первый вектор на оси Ох, пусть его координаты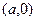 
, второй вектор 
. Тогда их скалярное произведение равно 
. С другой стороны, произведение модулей на косинус угла:
.
Векторное произведение.
Определение. Вектор 
называется векторным произведением векторов 
, обозначается 
, если выполнены 3 условия:
1) 
, 
.
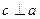2) Векторы 
образуют правоориентированную тройку, то есть с конца вектора 
кратчайший поворот от 
к 
виден против часовой стрелки.
3) 
параллелограмма, образованного парой векторов 
, то есть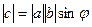 
.
Таблица свойств скалярного и векторного произведений:
сходство и различия.
| 
|
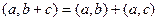
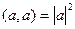
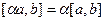
Метод нахождения векторного произведения с помощью определителя: Можно записать в 1-ю и 2-ю строку исходные два вектора, в третьей строке добавить произвольные обозначения осей 
, и вычислить этот определитель.
= 
. Миноры порядка 2 вычислятся, эти числа как раз и будут координатами 
нового вектора, который является векторным произведением.
Пример. Найти векторное произведение векторов (1,1,1) и (1,2,3)
= 
= 
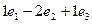. Ответ (1,-2,1).
Также можно проверить, что он действительно перпендикулярен исходным векторам (скалярно умножить на 1-й или на 2-й вектор, получим 0).
Примечание. Определитель можно вычислять либо разложением по 3-й строке, либо ранее известными методами, в том числе добавить копии двух первых столбцов справа.
Смешанное произведение. Определеятся так: 
.
Этот объект корректно определён и существует: векторное произведение первой пары есть какой-то вектор, и его можно скалярно умножить на ещё один, третий вектор, в итоге получится константа.
Смешанное произведение вычисляется с помощью определителя так: 
.
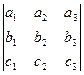Обоснование: Если рассмотреть разложение этого определителя по третьей строке, то получится
, то есть 1-я координата векторного произведения 
как раз и умножается на 1-ю координату вектора , 2-я на 2-ю и т.д. то есть это и есть 
.
Геометрический смысл: объём параллелепипеда, образованного тремя векторами.
ЛЕКЦИЯ № 4. 17.09.2019
Глава 2. СИСТЕМЫЛИНЕЙНЫХ УРАВНЕНИЙ
Введение, основные методы решения
Список вопросов на доказательства (к экзамену).
Лекция 1.
1. Докажите, что модуль определителя квадратной матрицы 2 порядка равен площади параллелограмма, построенного на этих векторах.
2. Докажите, что 
(выполнить для матриц порядка 2).
3. Докажите, что существует n! перестановок порядка n.
Лекция 2.
4. Доказать свойство определителя: Если все элементы какой-либо строки представлены в виде сумм двух элементов, то определитель равен сумме двух определителей, где в первом из них в этой строке - первые слагаемые, а во втором - вторые.
5. Доказать свойство определителя: Если к любой строке прибавить другую строку, домноженную на число, 
не изменится.
6. Теорема. Если матрица треугольная, то 
.
7. Лемма. Если 
и 
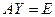, то 
.
8. Теорема. Обратная матрица 
существует тогда и только тогда, когда А невырожденная.
Лекция 3.
9. Теорема. Система линейно зависима 
хотя бы один из векторов этой системы является линейной комбинацией остальных.
10. Если система векторов содержит вектор 
, то она ЛЗС.
Литература.
1. Л.И.Магазинников, А.Л. Магазинникова. Линейная алгебра. Аналитическая геометрия. Учебное пособие https://edu.tusur.ru/publications/2244
2. Л.И.Магазинников, А.Л.Магазинников. Дифференциальное исчисление. Учебное пособие https://edu.tusur.ru/publications/2246
3. Магазинников Л.И. Высшая математика I. Практикум по линейной алгебре и аналитической геометрии: Учебное пособие Томск: ТУСУР, 2007. - 162 с.
Все учебные пособия кафедры математики можно найти на сайте кафедры по ссылке: https://math.tusur.ru/book.html