Скалярным произведением векторов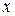 
и 
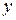называется число (скаляр), обозначаемое как 
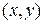(или просто 
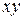) и определяемое соотношением
.
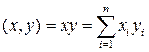Основные свойства этой операции
1. свойство симметрия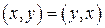 
;
2. дистрибутивное свойство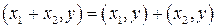 
;
3. 
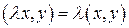для любого вещественного 
;
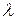4. 
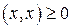, причём 
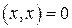тогда и только тогда, когда 
.
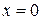Величина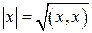 
называется модулем (длиной)вектора .
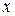Для любых двух векторов 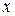и 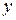справедливо неравенство Коши-Буняковского 
.
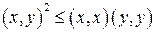Векторы 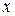и 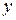называются коллинеарными, если 
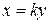. Практически это означает, координаты этих векторов пропорциональны.
Векторы 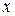и 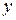называются ортогональными, если их скалярное произведение равно нулю: 
.
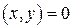Вещественное линейное пространство называется евклидовым пространством, если в нём определено скалярное произведение элементов. В евклидовом пространстве удобно использовать базис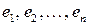 
, все элементы которого взаимно ортогональны и имеют единичную длину, т.е.
,
где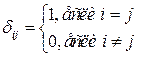 
- символ Кронекера.
Такие базисы называются ортонормированными и существуют в любом евклидовом пространстве. В ортонормированном базисе координаты вектора 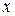можно представить в виде 
, а разложение вектора по базису
.
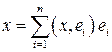Введение в рассмотрение скалярного произведения позволяет в дальнейшем использовать такие геометрически содержательные понятия, как ортогональность, угол и длина. Эти свойства широко используются при объяснении (обосновании и изложении) метода наименьших квадратов, в частности получении системы нормальных уравнений, а также для объяснения свойств МНК – оценок.
3. Матрицы, операции над матрицами.
Прямоугольная таблица чисел, содержащая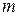 
строк и 
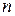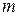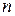столбцов, называется матрицей (точнее, числовой матрицей). Пара чисел и называются размером (порядком) матрицы. Обозначаются матрицы следующим образом: 
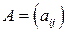или
|
|
.
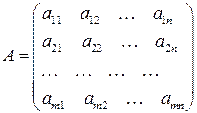Числа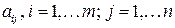 
, составляющие матрицу, называются её элементами.
В случае, если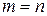 
, матрица называется квадратной, а число 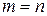- порядком матрицы.
Матрицу размера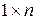 
называют матрицей – строкой, а матрицу размера 
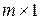- матрицей – столбцом. Очевидно, что матрица размера 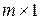может рассматриваться как элемент векторного пространства 
.
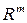Главной диагональю квадратной матрицы размера 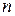называется совокупность элементов 
.
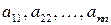Квадратная матрица называется диагональной, если все её элементы, не лежащие на главной диагонали, равны нулю. Диагональная матрица, все диагональные элементы которой равны единице, называется единичной и обозначается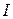 
.
Две матрицы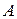 
и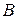 
называются равными, если они одинакового размера и соответствующие элементы равны.
Определим основные операции над матрицами.
Суммой матриц 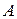и 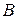одинакового размера называется матрица того же размера, определяемая равенством
,
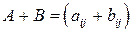т.е. при сложении матриц их соответствующие элементы складываются.
Произведением матрицы 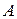на число 
называется матрица того же размера, определяемая равенством
,
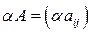т.е. при умножении матрицы на число все элементы этой матрицы умножаются на это число.
Операции сложения и умножение матриц на число обладают следующими свойствами:
· коммутативностью 
;
· сочетательное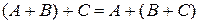 
;
· дистрибутивностью умножения на число относительно суммы матриц 
;
· дистрибутивностью умножения относительно суммы чисел 
;
· сочетательным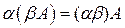 
.
Матрица, все элементы которой равны нулю, называется нулевой матрицей и обозначается 
. С помощью нулевой матрицы можно сформулировать такие свойства:
|
|
· 
.
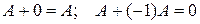Транспонированием матрицы 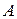называется операция, в результате которой меняются местами строки и столбцы матрицы с сохранением порядка их следования. Полученная в результате этой операции матрица называется транспонированной и обозначается 
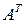. Таким образом
.
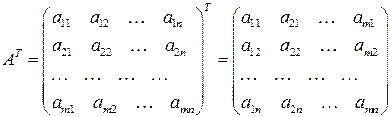Для операции транспонирования справедливы следующие очевидные свойства
· 
;
· 
.
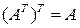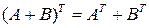Произведением матриц 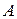размера 
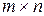и 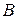размера 
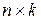называется матрица 
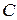размера 
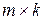(обозначается 
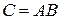), элементы которой определяются по формуле
.
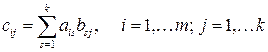В том случае, когда произведения матриц определены, будут справедливы следующие свойства:
· сочетательное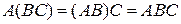 
;
· дистрибутивное относительно суммы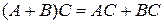 
или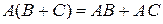 
;
· 
.
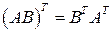Следует особо отметить, что в общем случае существование произведения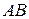 
не влечёт за собой существование произведения 
.
И даже в том случае, когда оба этих произведения 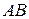и существуют, они могут не равняться друг другу. Матрицы, для которых выполняется равенство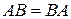 
, называются коммутативными.
Скалярное произведение двух векторов 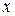и 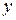удобно выразить в форме произведения матриц 
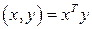. С другой стороны, элементы произведения матриц можно рассматривать как скалярные произведения строк первой матрицы на столбцы второй.
Рассмотрение столбцов матрицы 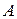размера 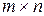в качестве 
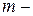мерных векторов позволяет установить их линейную зависимость. Максимальное число линейно векторов – столбцов матрицы 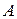называется рангом по столбцам. Аналогичным образом можно сформулировать понятие ранга по строкам – для этого достаточно перейти к рассмотрению транспонированной матрицы 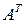. Доказывается, что ранг по столбцам матрицы 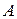равен рангу по строкам. Эта величина называется рангом матрицы 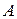и обозначается 
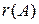. Очевидно (из определения следует,), что 
. Для нулевой матрицы полагают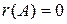 
.
|
|
Каждой квадратной матрице по определённому правилу можно поставить в соответствие число (обозначается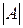 
или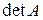 
), называемое определителем (детерминантом) матрицы. Для вычисления определителя матрицы 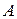можно использовать формулы
, 
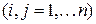
где 
- квадратная матрица порядка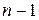 
, которая получается из матрица 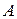вычеркиванием 
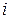-ой строки и 
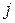-го столбца. Определитель 
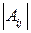называется минором элемента 
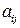. Приведённые формулы называются разложением определителя матрицы 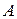по 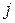-му столбцу и 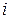-ой строке соответственно.
Свойства определителей, используемые при построении и исследовании эконометрических моделей, связаны с некоторыми действиями, которые не меняют его величины, а также позволяют установить равенство нулю определителя. Укажем основные из них.
· 
;
· 
;
· 
;
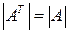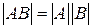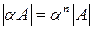· величина определителя не изменится, если к элементам одной строки (столбца) прибавить элементы другой строки (столбца), умноженные на одно и то же число;
· при перестановке любых двух строк (столбцов) величина определителя умножается на –1;
· величина определителя, содержащего две пропорциональные строки (столбца), равна нулю;
· сумма произведений элементов любой строки (столбца) на алгебраические дополнения другой строки (столбца) равна нулю, т.е.
.
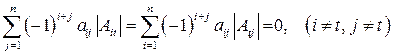Матрица 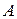называется невырожденной, если её определитель отличен от нуля. Всякая невырожденная матрица 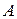имеет единственную обратную матрицу 
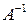, которая по определению удовлетворяет следующим равенствам
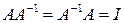
где 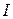- единичная матрица. Для обратных матриц основными являются свойства
· 
;
· 
;
· 
,
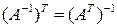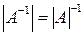которые выполняются, если только существуют все входящие в соответствующие равенства матрицы.
Собственным вектором квадратной матрицы 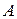порядка 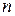называется ненулевой вектор 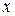, удовлетворяющий равенству
,
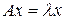где 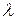- некоторое вещественное число. При этом число 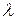называется собственным значением матрицы 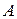, соответствующим собственному вектору .
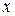Очевидно, что собственный вектор 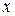определён с точностью до коэффициента пропорциональности, и поэтому обычно нормируется условием 
. Для нахождения собственных значений переходят к уравнению матричному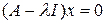 
, которое представляет собой однородную систему уравнений. Для существования ненулевого решения такой системы необходимо и достаточно, чтобы определитель системы равнялся нулю, т.е. 
.
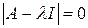Уравнение 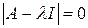называется характеристическим уравнением матрицы 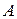. Корни этого уравнения будут собственными значениями матрицы 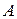. При этом учитывается кратность корней характеристического уравнения.
Если все корни характеристического уравнения простые, т.е. имеют кратность равную 1, то соответствующие им собственные векторы линейно независимы.
Приложение 2.
Элементы теории вероятностей и математической статистики: основные понятия и факты.
Изучение систематических курсов теории вероятностей и математической статистики является обязательным условием успешного освоения эконометрики. Справочный материал этого Приложения призван напомнить читателю основные понятия и терминологию этих предметов. Материал не претендует на полноту и математическую строгость изложения и ни коем образом не подменяет основных учебников в этой области.