· Нормальное распределение.
Это распределение полностью определяется математическим ожиданием μ и средним квадратическим отклонением s. Плотность нормального распределения записывается в виде:
,
где 
.
Кривая плотности нормального распределения имеет форму симметричного колокола, см. рис.П2.1.
Рис.П2.1.Кривая плотности и интегральная кривая нормального распределения при μ=1 иs=0,8
· Логнормальное распределение
Переменная называется логнормально распределенной, если ее логарифм нормально распределен. Такая ситуация возникает, когда рассматривают распределение произведения большого числа случайных, одинаково распределенных независимых величин. Обозначим за μ математическое ожидание и за s среднее квадратическое отклонение логарифма логнормального распределения. Тогда математическое ожидание и дисперсия самого логнормального распределения вычисляются по формулам:
M(Y) = 
; D(Y) = 
.
Из определения вытекает, что для плотности логнормального распределения справедливо соотношение
.
На рис.П2.2 отражены кривые плотности и интегральной функции логнормального распределения
Рис.П2.2.Кривая плотности и интегральная кривая логнормального распределения при μ=1 и s=0,8.
· 
-квадрат распределение
Пусть 
- нормальные независимые случайные величины с нулевым математическим ожиданием и единичной дисперсией. Тогда сумма квадратов этих величин 
имеет распределение с n степенями свободы. Плотность -распределения выражается формулой:
,
где Г(x)= 
- гамма функция, в частности Г(n+1)=n!.
На рис.П2.3 изображены кривые плотности и интегральной функции распределения
Рис.П2.3.Кривая плотности и интегральная кривая -распределения при n=10.
· Распределение Стьюдента
Пусть 
, а 
- распределенная по закону независимая от 
случайная величина с k степенями свободы. Тогда случайная величина 
распределена по закону Стьюдента (t -распределение) с k степенями свободы. На рис.П2.4 изображены графики кривых плотности и интегральной функции t -распределения с k =5 степенями свободы.
Рис.П2.4.Кривая плотности и интегральная кривая t -распределения при k=5.
· Распределение Фишера.
Если U и V независимые -распределенные случайные величины со степенями свободы n1 и n2, то величина
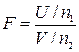
является распределением Фишера со степенями свободы n1 и n2.
Рис.П2.5.Кривая плотности и интегральная кривая F -распределения при n1=5 и n2=5.
Основные понятия математической статистики. Точечные оценки параметров.
В математической статистике исследуемую случайную величину, в общем случае – многомерную, принято называть генеральной совокупностью, а её реализации в последовательности независимых испытаний – выборкой из генеральной совокупности, или коротко – выборкой. Сами значения случайной величины принято называть элементами выборки, а их количество – объёмом выборки. Основной задачей статистического исследования является описание генеральной совокупности по имеющейся выборке. Как правило, эта задача сводится к нахождению закона распределения случайной величины 
или определению её числовых характеристик.
Статистикой называется любая функция элементов выборки 
. Очевидно, если рассматривать элементы выборки как независимые одинаково распределённые случайные величины, то и статистику следует рассматривать как случайную величину, имеющую свой закон распределения.
Любые характеристики случайной величины, полученные по выборке, называются выборочными или эмпирическими. Статической оценкой называется выборочная характеристика, используемая в качестве приближённого значения неизвестной характеристики генеральной совокупности. Так, статистической оценкой плотности распределения непрерывной случайной величины является гистограмма.
Статистическая оценка, представленная в виде числа – точки на числовой прямой, называется точечной. Пригодность использования в приложениях точечной оценки зависит от наличия у неё таких свойств как несмещённость, состоятельность, эффективность.
Пусть - случайная выборка и 
выборочная оценка некоторого параметра 
. Оценка 
называется несмещенной, если для любого фиксированного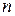 
выполняется равенство 
. Это равенство гарантирует, что использование этой оценки не приводит к систематическим ошибкам.
Оценка называется состоятельной, если она сходится по вероятности к значению параметра , т.е. выполняется условие 
для любого 
. Выполнение этого условия означает, что с увеличением объема выборки возрастает наша уверенность в малом по абсолютной величине отклонении оценки от истинного значения параметра .
Оценка называется эффективной, если она обладает наименьшей дисперсией по сравнению с любыми другими оценками. Эффективная оценка является наилучшей в смысле минимума среднеквадратичного отклонения оценки от истинного значения параметра .
В качестве оценки математического ожидания принято использовать среднее выборочное
Эта оценка является несмещённой, состоятельной, а в случае нормального распределения генеральной совокупности – эффективной.
Несмещенной, состоятельной оценкой дисперсии является выборочная (исправленная) дисперсия
.
Выборочная ковариация определяется формулой
,
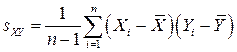где 
и 
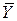- выборочные средние величин и 
соответственно. Величина 
является выборочной оценкой коэффициента ковариации 
. Оценкой коэффициента корреляции является выборочный коэффициент корреляции
.
И нтервальные оценки и проверка статистических гипотез.
Интервальной оценкой параметра называется интервал 
, который с заданной вероятностью 
(
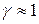) накрывает неизвестное значение . При этом сам интервал называется д оверительным, а вероятность - доверительной или уровнем надежности. Величина 
называется уровнем значимости.
Для построения интервальной оценки параметра необходимо знать закон распределения статистики и задать уровень надёжности . Границы доверительного интервала определяются условием
.
Доверительный интервал для математического ожидания нормально распределенной случайной величины , построенный по выборке на уровне надёжности имеет вид
,
где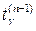 
- двусторонняя - квантиль распределения Стьюдента с 
-ой степенью свободы, а 
- среднеквадратичное отклонение выборочной средней.
Доверительный интервал для дисперсии нормально распределенной случайной величины с заданным уровнем надежности определяется следующим образом:
,
где 
и 
- квантили уровней 
и 
распределения 
, т.е. величины, удовлетворяющие соотношениям 
и 
.
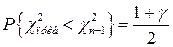Статистической гипотезой принято считать любое предположение о законе распределения случайной величины генеральной совокупности или о значениях параметров закона распределения. Высказанное предположение, которое подлежит проверке, обозначается 
и называется основной или нулевой гипотезой. Наряду с основной гипотезой в рассмотрение вводится и противоречащая ей гипотеза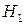 
, которая называется конкурирующей или альтернативной 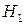. Цель проверки статистической гипотезы заключается в том, чтобы установить, не противоречит ли высказанная гипотеза имеющимся выборочным данным .
Для проверки нулевой гипотезы формируется статистический критерий - специальная статистика 
, распределение которой в условиях известно. По известному распределению статистического критерия определяется множество значений, которые величина 
принимает с вероятностью , близкой к единице, т.е. практически достоверно. Это множество называется областью принятия нулевой гипотезы . Дополнение этого множества образует критическую область (или область отвержения ).
Проверка нулевой гипотезы осуществляется следующим образом. По выборочным данным вычисляется значение критерия 
. Если значение 
принадлежит критической области, то проверяемая гипотеза отвергается, как противоречащая выборочным данным, и принимается альтернативная гипотеза 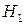. Если же принадлежит области принятия нулевой гипотезы, то принимается гипотеза как не противоречащая имеющимся данным. В этом случае говорят, что нулевая гипотеза принимается на уровне значимости .
Уровень значимости 
характеризует вероятность совершить ошибку первого рода, заключающуюся в напрасном отвержении имеющей место нулевой гипотезы - 
. Ошибкой второго рода называется ошибка принятия ложной гипотезы .
В компьютерных системах, в частности в STATISTICA, для выборочного значения критерия определяется уровень значимости нулевой гипотезы 
(или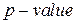 
- 
-значение), величина которого определяется условием 
. Это значение характеризует вероятность ошибки, связанной с распространением утверждения нулевой гипотезы на всю генеральную совокупность. Чем меньше - значение, тем увереннее происходит отвержение основной гипотезы. В практических задачах в качестве стандартного уровня принят 5%-ый уровень значимости.
В заключение укажем на принцип двойственности теории построения доверительных интервалов и проверки гипотез о значениях параметров распределения. Нетрудно убедиться в том, что при выбранном уровне надежности доверительный интервал для некоторого параметра составляют те значения параметра, которые совместимы с гипотезой 
при уровне значимости .
Приложение 3