Гетероскедастические модели (ОАРУГ - модели).

В 1986 году Болеслев [ 23 ] обобщил работу Энгла предположив, что условная дисперсия может представлять АРСС - процесс. В этом случае ошибки наблюдений описываются формулой

 

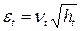, (11.17)

где s_n² =1 и

 

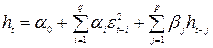(11.18)

Так как n_t - белый шум не зависящий от прошлых реализаций e_t-i, то условные и безусловные средние e_t равны нулю. Важным моментом является формула условной дисперсии для e_t:

 

M_t-1e_t² = h_t . (11.19)

 

Обобщенная АРУГ(p,q) - модель (ОАРУГ - модель) позволяет ввести авторегрессионые компоненты и слагаемые типа скользящего среднего в гетероскедастическую дисперсию.

Выгода от применения ОАРУГ - моделей ясна, также применение этих моделей может придать более экономный и простой вид описанию модели. Более экономные модели содержат меньше коэффициентов для оценивания и, значит, меньше ограничений на эти коэффициенты.

Ключевым моментом в ОАРУГ - моделях является тот факт. что возмущения {y_t}- последовательности образуют АРСС - процесс. Например, мы оцениваем {y_t} - последовательность с помощью некоторой АРСС - модели. Если модель адекватна, то АКФ и ЧАКФ остатков будут указывать на белый шум. Однако, АКФ квадратов остатков могут помочь идентифицировать порядок ОАРУГ - процесса. Так как

M_t-1e_t² = h_t, то перепишем (11.18) в виде

(11.20)

Уравнение (11.20) представляет АРСС - процесс для {e_t²} - последовательности. Если присутствует в процессе условная гетероскедастичность, то коррелограмма квадратов остатков будет удовлетворять условиям именно такой модели. Техника построения коррелограммы следующая:

1. Оцениваем {y_t} - последовательность с помощью лучшей из АРСС - моделей, как это описано в десятой главе. Найдем e_t²-квадраты ошибок модели. Вычисляем выборочную дисперсию остатков s² по формуле

 

, где T - число остатков.

2. Вычисляем и графически изображаем выборочные автокорреляции квадратов остатков по формуле:

 

.

 

3. Для больших выборок стандартное отклонение r(i) может быть приближенно взятым равным Т^-1/2. Если значение r(i) значительно отличается от нуля, то это свидетельствует о наличии ОАРУГ -процесса.

Как и в главе 10, Q-статистика

имеет c² - распределение с n - степенями свободы, если e_t² не коррелированы. Если эта гипотеза отвергается, то это свидетельствует о необходимости принять ОАРУГ - модель. На практике обычно полагают n =T/4.

Более строгий тест, использующий мультипликатор Лагранжа, для обнаружения существования АРУГ - процесса предложил Энгл в 1982 году. Его методология включает два шага:

1. МНК - оценку наиболее подходящей АР(n) -модели

 

y_t = a₀ + a₁y_t-1 + a₂y_t-2+...+a_ny_t-n +e_t.

 

2. Вычисляем квадраты ошибок модели e_t². Строим авторегрессию порядка q квадратов остатков

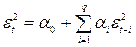. (11.21)

Если не подходит ни одна из АРУГ моделей, то все a_i (i = 1,...,q) равны нулю и R² -статистика будет мала. Статистика будет сходится к c_q² - распределению. Если больше критического значения c_q² - распределения при заданном уровне значимости, то это свидетельствует о необходимости принять АРУГ - гипотезу.

 

11.3 АРУГ-М модели

Энгл, Лилиен и Робинс [26] обобщили АРУГ - модель, позволив среднему процесса зависеть от собственной условной дисперсии. Этот класс моделей, названный АРУГ-М - моделями удобен для изучения рынка ценных бумаг. Основная мысль состоит в том, что избегающие риска агенты (участники рынка) будут требовать компенсацию за то, что держат в своем портфеле рискованные ценные бумаги. Известно, что степень риска часто измеряется дисперсией доходности, поэтому премия за риск будет возрастающей функцией условной дисперсии доходности. Энгл с соавторами выразили эту мысль, выписав превышение доходности y_t от держания рискованных ценных бумаг над государственными облигациями, рассчитанными на погашение в течение одного периода времени принятого за единицу, в виде:

y_t = m_t + e_t, (11.22)

где m_t - премия за риск, побуждающая избегающих риска агентов держать долгосрочные ценные бумаги, а не краткосрочные государственные облигации; e_t - непредсказуемые колебания доходностей долговременных рискованных ценных бумаг.

Заметим, что ожидаемое превышение доходностей от держания долгосрочных ценных бумаг должно быть равно премии за риск

M_t-1y_t = m_t. (11.23)

Энгл, Лилиен и Робинс предполагали, что премия за риск является возрастающей функцией условной дисперсии e_t; другими словами, чем больше условная дисперсия доходностей, тем большая компенсация необходима участнику рынка, чтобы продолжать держать долгосрочные ценные бумаги. Математически это означает, что

m_t = b + dh_t, d > 0, (11.24)

 

где h_t - условная дисперсия e_t. Выразим h_t как АРУГ - процесс

 

. (11.25)

 

Система уравнений (11.22),(11.23),(11.24),(11.25) образуют основу АРУГ-М модели.

Если рассмотреть случай a₁= a₂=... = a_q=0, то АРУГ-М модель вырождается в хорошо известную модель с постоянной премией за риск. Как и в предыдущих случаях, принятие АРУГ-М модели может быть осуществлено на основании теста, использующего выражение типа (11.21). Статистика асимптотически распределена как c² с числом степеней свободы равным числу ограничений.

Используя поквартальные данные с 1960:1 до 1984:2, Энгл, Лилиен и Робинс (1987) построили превышение доходностей государственных шестимесячных облигаций над трехмесячными. Пусть r_t - обозначает квартальную доходность трехмесячных облигаций за период от t до t+1. В конце двух кварталов, вложив $1 инвестор получит (1+ r_t)(1+ r_t+1) долларов. Пусть R_t означает квартальную доходность от шестимесячных облигаций. Тогда (1+R_t)², это доход, полученный держателем шестимесячной облигации в конце срока хранения. Превышение от держания шестимесячной облигации (без учета квадратичных членов) приблизительно составит

y_t = 2R_t - r_t+1- r_t. (11.26)

Подставляя y_t в виде константы плюс возмущение, получаем уравнение

y_t = 0.142 + e_е (11.27)

(4.04) (в скобках дана t- статистика свободного члена).

Это превышение 0,142% за квартал составило четыре стандартных отклонения от нуля. После 1979 года наступил период более высокой изменчивости, чем в предыдущем периоде наблюдений. Чтобы тестировать наличие АРУГ ошибок, квадратичные ошибки были представлены регрессией со взвешенным средним квадратичных ошибок:

 

h_t = a₀ +a₁(0,4e²_t-1 + 0,3e²_t-2 +0,2e²_t-3 +0,1e²_t-4 )

 

При гипотезе a₁ = 0 получено значение = 10,1, которое должно быть распределено как χ² c одной переменной степенью свободы. При 1% уровне значимости, критическое значение χ² - распределения равно 6,635. Следовательно, гетероскедастичность присутствуют без сомнения.

Итак, существуют АРУГ - ошибки и, следовательно, уравнение (11.27) не отражает суть процесса.

Оценки коэффициентов по методу максимального правдоподобия (ММП - метод) АРУГ - М модели и соответствующие t - статистики цитируемой работы приводятся ниже

 

y_t = -0,0241 + 0,687h_t +e_t

t (-1,29) (5,15)

 

h_t = 0,0023 + 1,64(0,4e²_t-1 + 0,3e²_t-2 + 0,2e²_t-3 + 0,1e²_t-4)

t (1, 08) (6,3)

 

Оценка 1,64 параметра АРУГ-уравнения показывает, что безусловная дисперсия бесконечная (хотя условная дисперсия конечная). Изменения в величине e_t-i ведут к увеличению условной дисперсии. Поэтому и появляются периоды спокойствия и высокой изменчивости. В течение периода высокой изменчивости, премия за риск растёт.

11.4 ММП - оценивание ОАРУГ и АРУГ - М моделей.

В этом пункте мы описываем метод максимума правдоподобия необходимый для понимания и написания программ для АРУГ моделей.

Предположим, что значения íy_tý последовательности нормально распределены со средним m и постоянной дисперсией s². Из теории вероятностей следует, что логарифм функции правдоподобия, использующей Т независимых наблюдений, распределенных по нормальному закону, имеет вид

 

,

где L - функция правдоподобия.

Задача состоит в максимизации функции правдоподобия по неизвестным параметрам m и s по известным выборочным данным íy_tý. Приравнивая нулю частные производные первого порядка, имеем

 

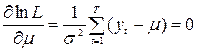
Решая систему уравнений относительно m и s, получаем

 

m* = å y_t/T,

s² = å (y_t- m*)²/T.

Те же принципы применяются и в регрессионном анализе.

Предположим, что последовательность {e_t} получена из модели

e_t = y_t- bx_t.

В классической регрессионной модели среднее e_t предполагается равным нулю, а дисперсия равной s², и различные реализации {e_t} независимы и подчинены нормальному распределению вероятностей. Тогда функция правдоподобия принимает вид:

.

 

Максимизируя по s² и Т, получаем стандартные формулы МНК для коэффициентов регрессии

s² = å (e_t)²/T,

b* = å x_ty_t/ å(x_t)².

До сих пор мы получали линейные относительно неизвестных условия первого порядка. К сожалению, для АРУГ- моделей условия первого порядка оказываются нелинейными и их решение требует некоторых более сложных алгоритмов.

Например, рассмотрим АРУГ(1) процесс для ошибок регрессионной модели. Будем снова предполагать,что

e_t = y_t- bx_t, но e_t представимо в виде:

и,поэтому, условная дисперсия e_t равна

h_t = a₀ +a₁e_t-1².

Хотя условная дисперсия e_t не постоянна, легко ввести необходимые поправки в функцию правдоподобия

,

где

h_t= a₀ +a₁e_t-1² = a₀ +a₁(y_t-1 - bx_t-1)².

Следует максимизировать функцию относительно a₀, a₁ и b. Многие компьютерные программы позволяют провести такую максимизацию итерационными методами.

В заключение главы, заметим, что для построения эконометрических моделей с изменяющейся дисперсией существуют, кроме специализированного пакета E-Views и соответствующего модуля пакета МАТЛАБ, богатая по возможностям, распространяемая бесплатно для российских пользователей, программа MATRIXER, автор Александр Цыплаков (https://www.matrixer.narod.ru/).

11.5. Контрольные вопросы к главе 11.

1. Чем была вызвана необходимость исследования моделей с условной гетероскедастичностью?

2. Дайте определение АРУГ моделей, какому процессу подчиняется в этих моделях условная дисперсия ошибки исходного временного ряда.

3. Покажите, что прогнозы для M_t-1(e_t)² модели (11.16) имеют вид авторегрессии порядка q, то есть являются процессами вида

M_t-1(e_t)² = a₀ +Sa_ie_t-i² .

4. Дайте определение ОАРУГ –модели. Какие отличия в поведении условной дисперсии остатков АРУГ моделей и ОАРУГ –моделей.

5. Опишите область применения АРУГ-М модели и ее отличия от АРУГ моделей.

6. Опишите метод максимального правдоподобия для оценок коэффициентов АРУГ-модели Энгла (11.4, 11.11).