Геометрическая интерпретация метода наименьших квадратов

Для геометрического вывода условий, которым должны удовлетворять оценки коэффициентов , рассмотрим частный случай исходных данных. Предположим, что имеются только два наблюдения, которые могут быть представлены в виде векторов и . Кроме этого будем предполагать, что прямая регрессионной модели проходит через начало координат, т.е. что . Заметим, что это предположение не является сколько-нибудь существенным, поскольку для его выполнения достаточно центрирования исходных данных. В этом случае уравнению будут соответствовать следующие геометрические построения, представленные на рисунке П.1.

 

2-ая

координата

 

 

 

 

 

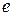
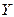
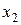
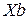
1-ая

координата

 

Рис П.1.. Геометрический вывод системы нормальных уравнений.

 

Вектор (или ) получается умножением вектора на число и, следовательно, будет коллинеарен вектору . Вектор будет равняться разности векторов и . Значение оценки вектора следует выбрать таким образом, чтобы модуль вектора был минимальным. Как следует из геометрических построений, минимальное расстояние от точки с координатами до прямой будет достигаться на перпендикуляре, опущенном из этой точки на указанную прямую. Следовательно, необходимым и достаточным условием минимизации будет условие ортогональност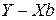и и . Известно, что необходимым и достаточным условием ортогональности двух векторов является равенство нулю их скалярного произведения. Таким образом, получаем уравнение 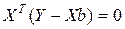, которое называется нормальным. Выполнив соответствующие преобразования, приходим в общем случае к системе нормальных уравнений

 

.

 

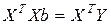Если матрица системы невырожденная, то существует обратная матрица 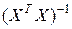, и система нормальных уравнений будет иметь решение

.

 

Оценки вектора , полученные при решении системы нормальных уравнений, называются оценками, полученными по методу наименьших квадратов, или, сокращённо – МНК-оценками. Зная значения решения , можно вычислить расчётные (прогнозные) значения переменной

.

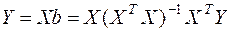Геометрически вектор является ортогональной проекцией вектора 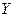на линейное пространство, натянутое на векторы , т.е. наилучшей аппроксимацией 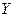линейной комбинацией векторов .

Из геометрических соображений также следует, что векторы и 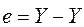ортогональны, и, следовательно, выполняется равенство

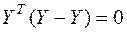или .

 

 

 

Приложение 4

Критические точки распределения Стьюдента

	Уровень значимости (двусторонняя критическая область)
0.10	0.05	0.02	0.01	0.002	0.001
	6.31 2.92 2.35 2.13 2.01 1.94 1.89 1.86 1.83 1.81 1.80 1.78 1.77 1.76 1.75 1.75 1.74 1.73 1.73 1.73 1.72 1.72 1.71 1.71 1.71 1.71 1.71 1.70 1.70 1.70 1.68 1.67 1.66 1.64	12.7 4.30 3.18 2.78 2.57 2.45 2.36 2.31 2.26 2.23 2.20 2.18 2.16 2.14 2.13 2.12 2.11 2.10 2.09 2.09 2.08 2.07 2.07 2.06 2.06 2.06 2.05 2.05 2.05 2.04 2.02 2.00 1.98 1.96	31.82 6.97 4.54 3.75 3.37 3.14 3.00 2.90 2.82 2.76 2.72 2.68 2.65 2.62 2.60 2.58 2.57 2.55 2.54 2.53 2.52 2.51 2.50 2.49 2.49 2.48 2.47 2.46 2.46 2.46 2.42 2.39 2.36 2.33	63.7 9.92 5.84 4.60 4.03 3.71 3.50 3.36 3.25 3.17 3.11 3.05 3.01 2.98 2.95 2.92 2.90 2.88 2.86 2.85 2.83 2.82 2.81 2.80 2.79 2.78 2.77 2.76 2.76 2.75 2.70 2.66 2.62 2.58	318.3 22.33 10.22 7.17 5.89 5.21 4.79 4.50 4.30 4.14 4.03 3.93 3.85 3.79 3.73 3.69 3.65 3.61 3.58 3.55 3.53 3.51 3.49 3.47 3.45 3.44 3.42 3.40 3.40 3.39 3.31 3.23 3.17 3.09	637.0 31.6 12.9 8.61 6.86 5.96 5.40 5.04 4.78 4.59 4.44 4.32 4.22 4.14 4.07 4.01 3.96 3.92 3.88 3.85 3.82 3.79 3.77 3.74 3.72 3.71 3.69 3.66 3.66 3.65 3.55 3.46 3.37 3.29
	0.05	0.025	0.01	0.005	0.001	0.0005
Уровень значимости (односторонняя критическая область)

 

 

Приложение 5

Критические точки распределения Фишера

(уровень значимости ;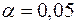

число степеней свободы большей дисперсии,

число степеней свободы меньшей дисперсии)

 

												¥
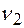
	18.5	19.0	19.2	19.2	19.3	19.3	19.4	19.4	19.4	19.4	19.4	19.4	19.5
	10.1	9.55	9.28	9.12	9.01	8.94	8.88	8.84	8.81	8.78	8.74	8.64	8.53
	7.71	6.94	6.59	6.39	6.26	6.16	6.09	6.04	6.00	5.96	5.91	5.77	5.63
	6.61	5.79	5.41	5.19	5.05	4.95	4.88	4.82	4.78	4.74	4.68	4.53	4.36
	5.99	5.14	4.76	4.53	4.39	4.28	4.21	4.15	4.10	4.06	4.00	3.84	3.67
	5.59	4.74	4.35	4.12	3.97	3.87	3.79	3.73	3.68	3.63	3.57	3.41	3.23
	5.32	4.46	4.07	3.84	3.69	3.58	3.50	3.44	3.39	3.34	3.28	3.12	2.93
	5.12	4.26	3.86	3.63	3.48	3.37	3.29	3.23	3.18	3.13	3.07	2.90	2.71
	4.96	4.10	3.71	3.48	3.33	3.22	3.14	3.07	3.02	2.97	2.91	2.74	2.54
	4.84	3.98	3.59	3.36	3.20	3.09	3.01	2.95	2.90	2.86	2.79	2.61	2.40
	4.75	3.88	3.49	3.26	3.11	3.00	2.92	2.85	2.80	2.76	2.69	2.51	2.30
	4.67	3.80	3.41	3.18	3.02	2.92	2.84	2.77	2.72	2.67	2.60	2.42	2.21
	4.60	3.74	3.34	3.11	2.96	2.85	2.77	2.70	2.65	2.60	2.53	2.35	2.13
	4.54	3.68	3.29	3.06	2.90	2.79	2.70	2.64	2.59	2.55	2.48	2.29	2.07
	4.49	3.63	3.24	3.01	2.85	2.74	2.66	2.59	2.54	2.49	2.42	2.24	2.01
	4.45	3.59	3.20	2.96	2.81	2.70	2.62	2.55	2.50	2.45	2.38	2.19	1.96
	4.41	3.55	3.16	2.93	2.77	2.66	2.58	2.51	2.46	2.41	2.34	2.15	1.92
	4.38	3.52	3.13	2.90	2.74	2.63	2.54	2.48	2.42	2.38	2.31	2.11	1.88
	4.35	3.49	3.10	2.87	2.71	2.60	2.51	2.45	2.39	2.35	2.28	2.08	1.84
	4.32	3.47	3.07	2.84	2.68	2.57	2.49	2.42	2.37	2.32	2.25	2.05	1.81
	4.30	3.44	3.05	2.82	2.66	2.55	2.46	2.40	2.34	2.30	2.23	2.03	1.78
	4.28	3.42	3.03	2.80	2.64	2.53	2.44	2.37	2.32	2.27	2.20	2.01	1.76
	4.26	3.40	3.01	2.78	2.62	2.51	2.42	2.36	2.30	2.25	2.18	1.98	1.73
	4.24	3.39	2.99	2.76	2.60	2.49	2.40	2.34	2.28	2.24	2.16	1.96	1.71
	4.17	3.32	2.92	2.69	2.53	2.42	2.33	2.27	2.21	2.16	2.09	1.89	1.62
	4.08	3.23	2.84	2.61	2.45	2.34	2.25	2.18	2.12	2.08	2.00	1.79	1.51
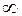
	3.84	3.00	3.60	2.37	2.21	2.10	2.01	1.94	1.83	1.83	1.75	1.52	1.00

 

Литература

 

1. Айвазян С.А., Мхитарян В.С. Прикладная статистика и основы эконометрики. - М.: ЮНИТИ, 1998.- 1022 с.

2. Айвазян С.А. Прикладная статистика. Исследование зависимостей / С.А. Айвазян, И.С. Енюков, Л.Д. Мешалкин. – М.: Финансы и статистика, -1985. - 487 с.

3. Арженовский С.В., Молчанов И.Н. Статистические методы прогнозирования. Учебное пособие/Рост.гос.экон.унив. - Ростов-н./Д.,-2001.-74с.

4. Боровиков В.П., Боровиков И.П. STATISTICA Статистический анализ и обработка данных в среде Windows. - М.: Изд-во Филинъ,-1997, -608 с.

5. Боровиков В.П., Ивченко Г.И. Прогнозирование в системе STATISTICA в системе Windows. Основы теории и интенсивная практика на компьютере: Учеб. пособие. – М.: Финансы и статистика, 1999.- 384 с.

6. Вайну Я.Я. Корреляция рядов динамики.- М.: Статистика. 1977.-С. 120

7. Гантмахер Ф.Р. Теория матриц. – М.1953, - 491 с.

8. Доугерти К. Введение в эконометрику / Пер. с англ. - М.: Инфра-М, 1997, - 401 с.

9. Дуброва Т.А. Статистические методы прогнозирования в экономике. – М.: МЭСИ, 2001. -52 с.

10. Ибрагимов Н.М. и др. Регрессионный анализ / Н.М. Ибрагимов, В.В. Карпенко, Е.А. Коломак, В.И. Суслов; Электронная версия https://econom.nsc.ru/jep/books/013/7.pdf — ЭФ НГУ, 1997.

11. Ильин В.А., Поздняк Э.Г. Линейная алгебра. – М.: Наука, 1978, - 304 с.

12. Кендал М., Дж. Стьюарт А. Многомерный статистический анализ и временные ряды. – М.: Наука, 1976. - 735 с.

13. Кремер Н.Ш., Пупко Б.А. Эконометрика: Учебник для вузов / Под ред. проф. Н.Ш. Кремера. – М.: ЮНИТИ-ДАНА, 2002. 311 с.

14. Лугачев М.И., Ляпунцов Ю.П. Методы социально-экономи­ческого прогнозирования. – М.: МГУ, ТЕИС, 1999. – 155 с.

15. Луговская Л.В. Эконометрика в вопросах и ответах: учеб. пособие.-М.:ТК Велби, Изд-во Проспект, 2005.- 208с.

16. Лукашин Ю.П. Регрессионные и адаптивные методы прогнозирования. Учеб. пособие.- М.: МЭСИ, 1997.

17. Носко В.П. Эконометрика. Введение в анализ временных рядов: Курс лекций.-М..2002//https://www/iet/ru/mipt/2/text/curs­­­_econometrics_lectures/htm

18. Магнус Я.Р. и др. Эконометрика: Начальный курс: учеб.- 4-е изд. / Я.Р. Магнус, П.К. Катышев, А.А. Пересецкий. - М.: Дело, 2000. -400 с.

19. Магнус Я.Р., Нейдеккер Х. Матричное дифференциальное исчисление с приложениями к статистике и эконометрике: Пер. с.англ./ Под ред. С.А. Айвазяна. – М.:ФИЗМАТЛИТ, 2002. – 496 с.

20. Четыркин Е.Н. Статистические методы прогнозирования. - М.: Статистика, 1975.

21. Эконометрика: Учебник для вузов.- 2-е изд, перераб. и доп./А.И. Орлов.-М.:Издательство «Экзамен»,2003-576с.

22. Эконометрика: Учебник/ Н.П.Тихомиров, Е.Ю. Дорохина –М.:Издательство «Экзамен», 2003.-512с.

23. Эконометрика: Учебник / Под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп.- М.: Финансы и статистика, 2005. - 576 с.

24. Bolleslev, Tim “Generalized Autoregressive Conditional Heteroscedasticity”, Journal of Econometrics 31, (1986), pp.307-327.

25. Box, Georg and Gwilym Jenkins. Time Series Analysis, Forecasting, and Control. San Francisco, Calif.: HoldenDay,1976.

26. W. Enders. Applied econometric time series, John Wiley and sons, Inc., 1995. – 433 p.

27. Engle, Robert., David Lilien, and Russel Robins “ Estimating Time Varying Risk Premia in the Term Structure: The ARCH-M Model”, Econometrica 55 (March 1987), pp. 391-407.

28. Engle,R.F. and Granger, C.W.J. Cointegration and Error Correction: Representation, Estimation and Testing, Econometrica,55 (1987), pp.251-276.

29. James D. Hamilton. Time Series Analysis//Prinston Univ.Press, Prinston, New Jersey, 1994-407p.

30. Granger C. W. J. Essays in econometrics: collected papers of Clive W. J. / C. W. J. Granger. In 2 vol. Vol. 2. Causality, integration and cointegration and long memory / C. W. J. Granger; ed. by E. Ghysels, N. R. Swanson, M. W. Watson. Cambridge; New York: Cambridge University Press, 2001. 378 p.

31. Greene, William H. Econometric Analysis, 5-th ed. //Prentice Hall, NY, 2003 - 1052p.

32. Makridakis S. G. Empirical evidence versus personal experience // Journal of Forecasting. – 1983. - № 2. - p. 295 – 306.

33. Makridakis S., Andersen A., Carbone R., Fildes R., Hibon M., Lewandowski R., Newton J., Parzen R., & Winkler R. The accuracy of extrapolation (time series) methods: Results of a forecasting competition // Journal of Forecasting. -1982. - № 1. - Р. 11 - 153.

34. Laurent, S. and J.P.Peters, "G@RCH 2.2: an Ox Package for Estimating and Forecasting Various ARCH Models," Journal of Economic Surveys, 16 (2002, No.3), 447-485.

35. P. C. B. Phillips, Understanding spurious regressions in Econometrics, J. Econometrics 33 (1986), 311-340.

36. Terence C. Mills The Econometric Modelling Financial Time Series // Cambridge, University Press. – 1993. - 247 p.

37. Ruey S. Tsay Analysis of Financial Time Series//John Wiley & Sons. Inc., New York, 2002, -455 p.