РАЗНОСТНЫЕ СХЕМЫ
ДЛЯ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
Численные методы.
Для простейших краевых задач, сформулированных в различных курсах математической физики, приводятся некоторые точные решения. Задачи для нелинейных уравнений с коэффициентами достаточно сложного вида или даже линейные задачи, но в областях сложной формы, редко удается решить классическими методами. В таких случаях прибегают к приближенным методам. Обычно рассматривают два вида приближенных решений: аналитические и численные. Рассмотрим численные методы, основанные на разностной аппроксимации производных. Такой подход называют разностным методом, методом конечных разностей или методом сеток. Применение разностных методов основано на их универсальности и наличию хорошо разработанной теории.
Пусть требуется найти решение дифференциальной задачи
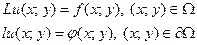. (1.1)
Задача (1.1) поставлена в некоторой области Ω с границей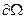 
. Здесь u – искомое решение уравнения; L – некоторый дифференциальный оператор, сокращенно обозначающий соответствующую дифференциальную операцию; f – правая часть уравнения (заданная функция). Как известно, для единственности решения уравнения к нему необходимо присоединить еще и краевые условия (начальные и граничные). Эти условия также записаны в виде символического равенства. Здесь ℓ – некоторый оператор, сокращенно обозначающий левую часть краевого условия; φ – правая часть краевого условия (заданная функция).
Пример 1. Рассмотрим задачу Дирихле для уравнения Лапласа в квадрате
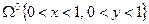с границей 
:
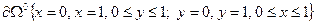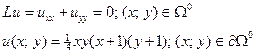
Таким образом, для поставленной задачи оператор L преобразует функцию u в дифференциальное выражение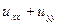 
.
В таких случаях пишут, что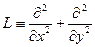 
: правая часть уравнения 
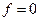; оператор граничных условий является тождественным оператором, т.е. он преобразует функцию u в u: 
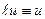; правая часть краевого условия имеет вид
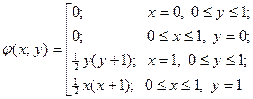
Разностный метод решения краевой задачи (1.1) можно представить в виде двух этапов:
1) построение разностной схемы, аппроксимирующей данную непрерывную задачу;
2) получение решения разностной задачи и оценка погрешности этого решения.
Суть метода состоит в следующем.
1. При построении разностной схемы первым шагом является замена области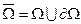 
непрерывного изменения аргументов областью дискретного их изменения – сеточной областью 
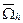(или просто сеткой), т.е. конечным (дискретным) множеством точек 
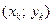называемых узлами сетки.
Пример 2. Для квадрата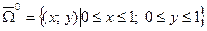 
сеточную область можно построить следующим образом. Проведем прямые линии 
.
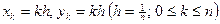Множество точек пересечения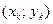 
этих прямых линий и составят сеточную область 
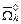, а сами точки образуют узлы сетки.
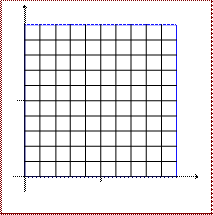
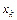
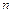
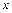
Рис. 1.1
Вместо функций непрерывного аргумента рассматриваются функции дискретного аргумента, определенные в узлах сетки и называемые сеточными функциями.
2. Второй шаг в построении разностной схемы состоит в аппроксимации производных, которые входят в дифференциальное уравнение и граничные условия, их разностными аналогами - линейными комбинациями значений сеточной функции в некоторых узлах сетки, называемых шаблоном.
3. Начальные и краевые условия тоже заменяются разностными начальными и краевыми условиями для сеточной функции.
4. При этом краевая задача для дифференциального уравнения заменяется дискретной краевой задачей (разностной схемой). Разностная схема представляет собой систему конечного числа линейных (если исходная задача была линейной) алгебраических уравнений. Следует иметь в виду, что для одной краевой задачи можно построить большое число различных разностных схем, среди которых далеко не все пригодны для использования на практике.
5. Если полученная таким образом разностная краевая задача разрешима и ее решение при измельчении сетки приближается (сходится) к решению исходной задачи для дифференциального уравнения, то оно и принимается за приближенное решение исходной задачи.
Несмотря на кажущуюся простоту метода, прежде чем приступить к решению конкретной задачи, необходимо уметь дать ответы на следующие вопросы:
1. Как выбрать сетку?
2. Как написать разностную схему на этой сетке?
Если эти вопросы решены, то важно иметь информацию по следующим вопросам:
1. Сколь хорошо разностная схема аппроксимирует исходную задачу?
2. Устойчива ли разностная схема и в каком смысле?
3. Какова скорость сходимости решения разностной задачи к решению исходной задачи?
4. Существует ли решение алгебраической системы и единственно ли оно; как это решение фактически вычислить (за возможно меньшее число действий).
Основные понятия и обозначения теории разностных схем
Сетка.
Исходным пунктом при построении разностных схемы является замена области непрерывного изменения аргумента некоторым конечным множеством точек, лежащих в этой области.
Это множество есть область определения функций дискретного аргумента; оно называется разностной сеткой.
Соответственно функции дискретного аргумента, определенные на этой сетке, носят название сеточных функций.
Рассмотрим простейшие примеры сеток.
Пусть область изменения аргумента x есть отрезок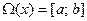 
. Для одномерной задачи простейшим примером пространственной разностной сетки является равномерное разбиение отрезка 
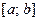на n равных частей, длина которых есть 
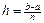(равномерная разностная сетка).
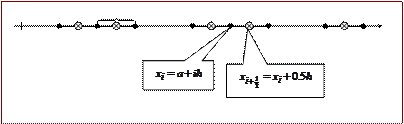
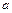
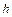
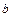
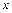
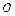
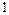
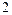
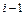
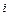
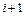
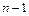
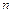
Рис. 1.2
Точки деления отрезка xi (на рис.1.2 отмечены кружками), число которых в данном случае составляет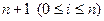 
, называют узлами сетки.
Расстояние между узлами сетки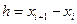 
есть шаг сетки.
Совокупность узлов составляет множество точек 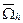, где определяются сеточные функции:
.
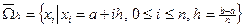Наряду с узлами, которые называют целыми точками, часто рассматривают так называемые " полуцелые точки "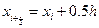 
(на рис.1.2 они отмечены крестиками). Множество полуцелых точек также можно использовать в качестве области определения сеточных функций.
Несмотря на кажущуюся простоту, вопрос о рациональном выборе сетки заслуживает внимания. С одной стороны, количество узлов сетки желательно брать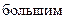 
, т.е. пользоваться мелкими, подробными сетками. Точнее передавая при этом область изменения дискретного аргумента, мы интуитивно рассчитываем лучше аппроксимировать непрерывное решение сеточными функциями. К тому же известные теоретические сведения о качестве разностных схем (аппроксимация, сходимость и т.д.) применимы, как правило, лишь для достаточно мелких сеток.
С другой стороны, практические соображения, и в первую очередь ограниченность быстродействия и объема памяти ЭВМ, заставляют обращаться к сеткам со сравнительно небольшим количеством узлов.
Подобная конфликтная ситуация типична для разностных методов и выбор разумного компромисса зачастую определяется не рекомендациями теории, а опытом и интуицией исследователя. Например, при выборе сеток часто используют неравномерные сетки. Если имеется априорная информация о решении, например, известно расположение некоторых его особенностей, для «разрешения» которых необходима мелкая сетка, то естественно, не увеличивая общего числа узлов, сгустить сетку в окрестности особенностей; в областях гладкости решения сетку можно сделать редкой. На рисунке 1.3 представлен пример неравномерной сетки – ее шаг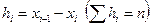 
выбран переменным с тем, чтобы наилучшим образом передать их решения 
.
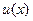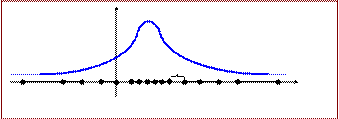
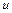
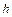
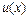
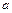
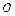
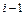
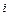
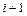
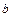
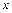
Рис. 1.3
В данном случае отрезок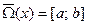 
разбит на n частей введением произвольных точек 
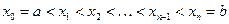. В результате имеем сетку
.
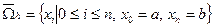Однако и такой прием не универсален, достаточно обратиться к случаю, когда особенность решения перемещается по сетке, причем закон ее движения, как это чаще всего бывает на практике, заранее неизвестен.
Пусть область изменения аргументов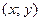 
есть прямоугольник
.
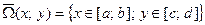Построим на отрезке 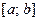сетку
и на отрезке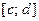 
сетку
.
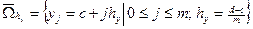Множество узлов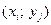 
с координатам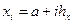и 
и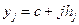 
назовем сеткой в прямоугольнике 
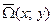и обозначим
.
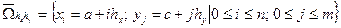Эта сетка равномерна по каждому из переменных x и y. Если хотя бы одна из сеток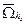 
или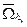 
неравномерна, то сетка 
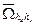называется неравномерной. Сетка 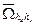, очевидно, состоит из точек пересечения прямых 
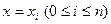и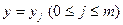 
.
Аналогично разностной сетке в пространстве определяется сетка по временной переменной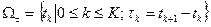 
; 
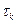− шаг сетки по времени, в общем случае зависящий от номера шага. Произведение сеток
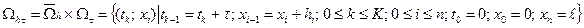
дает пространственно временную разностную сетку для численного решения одномерной нестационарной задачи.
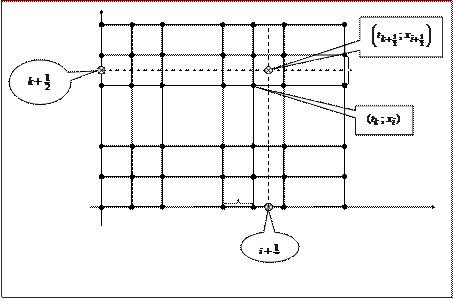
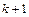
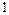
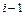
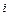
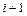
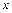
Рис. 1.4
Набор узлов 
и при фиксированном значении k называют k -м временным слоем сетки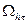 
.
Иногда рассматривают «полуцелые» слои, отвечающие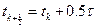 
. Узлы, расположенные на прямых вертикальных линиях 
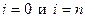, называют граничными.
Сеточные функции
Разностная задача строится с целью нахождения сеточной функции, определенной на введенной сетке и близкой к решению u соответствующей дифференциальной задачи. Сеточная функция есть функция дискретного аргумента, решение дифференциальной задачи u − функция непрерывного аргумента. Они принадлежат разным функциональным пространствам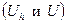 
. Поэтому возникает вопрос, как судить о степени близости этих функций.
Пусть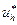 
– точное решение задачи (1.1) в узлах сетки 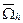, а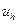 
– сеточная функция, которая является решением разностной задачи
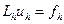. (1.2)
Как правило, вычислить 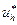не удается. Обычно поступают следующим образом. Рассматривают значения u в узлах сетки, что дает некоторую сеточную функцию 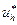, являющуюся, как говорят, проекцией решения u на пространство сеточных функций, и близость функций 
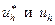характеризуют величиной 
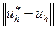, где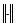 
− некоторая норма в пространстве сеточных функций. О близости решений разностной и дифференциальной задач можно говорить в том случае, когда величина 
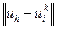неограниченно уменьшается при бесконечном дроблении сетки.
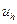Обозначим линейное нормированное пространство, образованное функциями 
, 
. Пространство, образованное функциями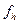 
(значения правой части дифференциального уравнения, подсчитанными в узлах сетки), 
.
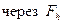Будем считать, что в пространствах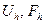 
, введены нормы 
.
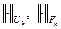Если
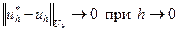, (1.3)
то говорят, что разностная схема является сходящейся.
Если для всех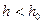 
имеет место неравенство
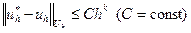, (1.4)
то говорят, что имеет место сходимость порядка k относительно h.
Значение сеточной функции u в некотором узле сетки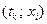 
будем обозначать 
: 
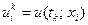. Соответственно 
.
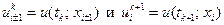Если взять равномерную норму, то имеем
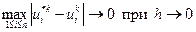(1.5)
или
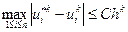. (1.6)
Разностная аппроксимация дифференциальных операторов
Основной момент в постановке разностной задачи состоит в переходе от дифференциальных уравнений, описывающих эволюцию сплошной среды, к соответствующим соотношениям для сеточных функций.
В классическом анализе производная от функции непрерывного аргумента определяется следующим образом
.
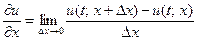Для функции дискретного аргумента на фиксированной сетке понятие подобного предельного перехода теряет смысл. При определении разностной производной вместо отношения бесконечно малых ограничиваются отношением конечных разностей.
Пусть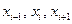 
− три последовательных узла равномерной разностной сетки по пространству с шагом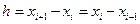 
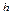
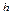
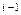
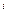
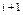
Рис. 1.5
Для аппроксимации производной в узле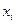 
(на k – временном слое) можно использовать следующие соотношения. Пусть функция 
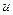задана, имеет нужное число производных 
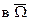и пусть приняты обозначения 
.
Тогда легко выводятся (например, с помощью формулы Тейлора) следующие формулы:
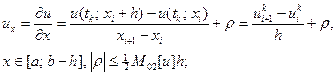(I)
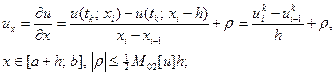(II)
Выражения (I), (II) называют односторонними разностными производными, (I) – правая производная (или производная вперед), (II) – левая производная (или производная назад).
Очевидно, правая производная в узле i является левой в узле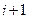 
.
Помимо соотношений (I), (I), использую также центральную, или двустороннюю разностную производную
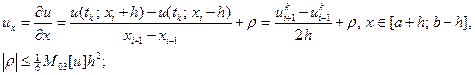(III)
Нетрудно проверить, что симметричное выражение (III) является полусуммой производных (I) и (I).
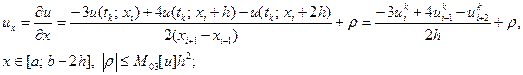(IV)
(V)
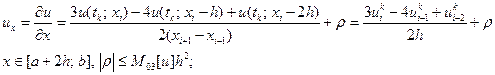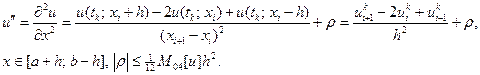(VI)
Для аппроксимации производной в узле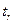 
(для фиксированного значения i) можно использовать следующие соотношения.
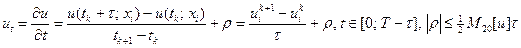; (VII)
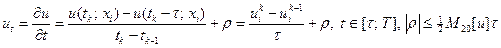; (VIII)
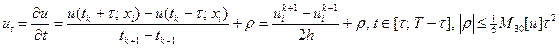. (IX)