1. Пусть требуется найти функцию 
, удовлетворяющую в некоторой области 
уравнению
, (3.1)
а на границе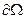 
области Ω условию
. (3.2)
Здесь 
и 
– заданные функции непрерывные в области 
.
Под решением краевой задачи понимается функция, непрерывная в области 
вместе с производными до второго порядка и удовлетворяющая уравнению (3.1) и граничным условиям во всех точках 
и 
соответственно. Как всегда, предполагается наличие единственного решения 
задачи (3.1), (3.2).
Переходим к описанию сеточного метода для этой задачи.
Хотя в практике встречаются сетки различного рода – параллелограммные, треугольные, шестиугольные – наиболее распространенными являются прямоугольные сетки. Только такими сетками мы будем пользоваться.
Изберем шаг 
по переменной x, шаг 
по переменной y, начальную точку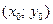 
и положим
.
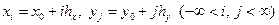Напишем уравнение (3.1) в произвольной точке 
, заменив частные производные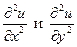 
, входящие 
оператор Лапласа, разностными отношениями по формуле VI
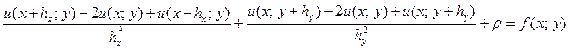. (3.3)
При этом для остаточного члена справедлива оценка
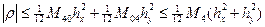. (3.4)
Здесь приняты обозначения
;
.
Разумеется, оценка (3.4) имеет смысл, если u имеет ограниченные производные 
.
Если обозначить 
и написать (3.3) для расчетной точки (узла) 
, мы получим
. (3.5)
Отбросив остаточный член, получим приближенное уравнение
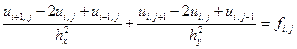. (3.6)
2. Будем искать приближенные значения 
для точного решения 
в узлах сетки 
, принадлежащих некоторой сеточной области 
с конечным числом узлов.
Желая написать уравнение (3.6) для некоторого узла 
, мы будем стараться соблюсти два условия:
1) узел должен принадлежать 
, так чтобы имели смысл символ 
;
2) Узлы 
должны также принадлежать области 
.
Четыре узла, о которых идет речь в условии 2), образуют вместе с узлом 
изображенный на рис. 3.1 «шаблон» (который в данном случае называется «крестом»).
Центральный узел 
играет особую роль, ибо левая часть (3.5) есть значение левой части уравнения (3.1) именно в этом узле. Назовем этот центральный узел расчетной точкой.
Мы будем говорить также, что изображенный на рис. 3.1 шаблон принадлежит расчетной точке .
Рис. 3.1
Назовем узел 
строго внутренним (для сеточной области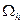 
), если все четыре вершины принадлежащего ему креста также принадлежат 
. Обозначим через символ 
некоторое подмножество , составленное из строго внутренних узлов 
, лежащих в замкнутой области (оно не обязано содержать все такие узлы). Это множество мы определим позднее. Множество всех остальных узлов назовем граничной полоской и обозначим 
.
Ясно (в силу конечности ), что существуют узлы, не являющиеся строго внутренними и потому принадлежащие полоске. Более того, если мы выберем какой-нибудь узел 
, и будем двигаться от него по линии сетки вверх или вниз, вправо или влево, то обязательно встретим узел граничной полоски (возможно, что таковым окажется сам узел 
).
Мы имеем теперь право, написать (3.6) для каждого узла 
.
Наша цель – определение 
для всех узлов . Пусть число узлов в области 
есть N, число узлов в области 
есть 
. Тогда для определения N неизвестных величин мы имеем 
уравнений (3.6). Дефицит в числе уравнений 
объясняется наличием узлов граничной полоски. Чтобы покрыть этот дефицит мы должны дополнительно составить 
уравнений – по одному на каждый узел граничной полоски. Эти уравнения мы будем составлять, используя граничные условия.
3. Для первой краевой задачи обозначим 
множество узлов сетки, принадлежащих . Строго внутренний узел 
отнесем к области 
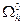, если не только он вместе с четырьмя вершинами своего креста принадлежит , но и два отрезка, соединяющие противоположные вершины креста, также принадлежат . Все прочие узлы отнесем к граничной полоске 
.
Мы должны, как это было уже сказано, каждому узлу граничной полоски соотнести линейное алгебраическое уравнение, связывающее значение 
в нескольких узлах. Присоединив их к уравнениям (3.6), написанным для каждого узла , мы получим систему, в которой число уравнений будет равно числу неизвестных, т.е. числу узлов.
Проще всего написать такое уравнение для узла 
, если он лежит на 
. Это уравнение естественно написать в форме
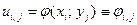, (3.7)
Иногда за счет выбора параметров сетки можно добиться того, что все узлы граничной полоски будут лежать на 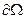, так что все добавляемые уравнения будут иметь простейший вид (3.7). Ясно, как это сделать, например, для прямоугольной области. Если это не удается, приходится вместо уравнений (3.7) писать равенства, учитывающие граничные условия приближенно. Это можно сделать по-разному.
а) 
б)
в) г)
Рис. 3.2
Пусть 
, но 
. По определению 
во множестве имеется точка, отстоящая от точки 
на расстояние, не большее 
. Пусть 
есть такая точка . Правило, по которому выбирается эта точка, здесь несущественно. Можно, например, в качестве точки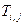 
брать ближайшую к точке 
точку 
. В первом варианте положим
.
Ясно, что 
– разность 
есть величина порядка расстояния между этими точками: 
. Эта оценка очевидным образом неулучшаема.
В первом варианте аппроксимация граничного условия оказывается значительно более грубой, чем аппроксимация дифференциального уравнения, где погрешность имеет второй порядок малости. Поэтому этот вариант применяется редко. Более распространен второй вариант, к изложению которого мы сейчас переходим.
По определению точки граничной полоски, на одном из отрезков, соединяющих точку 
с четырьмя вершинами креста, имеется точка, принадлежащая 
.
Обозначим через 
такую точку (так что отрезок 
лежит в области ). Обозначим через 
точку , соседнюю с точкой , и которая лежит на прямой линии в обратную от точки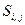 
сторону. На рис. 3.2 изображены четыре возможных случая а), б), в), г) расположения точек 
и 
.
Вернемся к рисунку 3.2. Здесь 
обозначена длина отрезка 
.
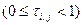Вычислим 
, используя формулу линейной интерполяции на отрезке 
по узлам 
. При очевидных обозначениях получаем уравнение
.
По известной формуле для погрешности линейной интерполяции получаем для случаев а), б) на рис. 3.2
.
Аналогичным образом для случаев в), г) на рис. 3.2 получим
.
Следовательно, справедлива в любом случае оценка
. (3.8)
Отбрасывая остаточный член и учитывая, что 
, получаем приближенное уравнение
.
Замечание. Если 
, то 
совпадают, 
, и эта формула переходит в (3.7).
Таким образом, останавливаясь на втором варианте учета граничных условий, мы получаем для первой краевой задачи систему сеточных уравнений
(3.9)
Получив сеточную систему (3.9), мы должны ее решить, если это возможно. Пусть 
есть решение этой системы. Тогда 
принимается за приближение к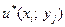 
.
4. Перейдем к вопросу о решении системы линейных алгебраических уравнений, к которому метод сеток сводит решение краевой задачи.
Вопрос этот имеет особо большое значение, ибо мы здесь имеем дело с системами с большим количеством уравнений. Системы эти обладают большими числами обусловленности 
, что создает дополнительные сложности.
Методы, которые мы рассматриваем в этом разделе, принадлежат к числу наиболее простых методов. Однако в настоящее время разработаны и, как правило, применяются существенно менее трудоемкие методы, которыми мы не имеем возможности заниматься. Речь идет, в первую очередь, о методах типа метода переменных направлений, с которыми можно ознакомиться в специальных руководствах, как например, Н. Н. Яненко, Метод дробных шагов решения многомерных задач математической физики, 1967; А. А. Самарский, Введение в теорию разностных схем, 1971.
Рассмотрим сначала итеративный метод. Приведем систему (3.9) к виду, удобному для проведения итераций:
(3.10)
Итеративный процесс
является сходящимся.
Говорить о методе исключения Гаусса здесь трудно, так как проведение метода Гаусса зависит от порядка, в котором расположены уравнения. В данном случае уравнения занумерованы не числами, а парами чисел 
или узлами сетки – каждый узел сетки выступает как расчетная точка для одного из уравнений системы (3.9). Эта система является весьма «редкой» – в каждом уравнении не более 5 ненулевых коэффициентов. Однако если применять метод Гаусса, то при неудачной нумерации уравнений это достоинство исходной системы будет в больше или меньшей степени теряться в системах, получаемых после нескольких шагов исключения.
Для решения системы (3.9) часто используется так называемый «метод прогонки ». Мы рассмотрим этот метод для простейшего случая, когда есть прямоугольник, стороны которого проходят по линиям сетки. В этом случае метод прогонки естественно трактовать как блочный метод Гаусса.
Существо блочного метода Гаусса можно описать в общем виде. Пусть требуется решить систему
линейных алгебраических уравнений. Разобьем матрицу системы A 
размером 
. Соответственно разобьем векторы правых частей и неизвестных на M «кусков» размером N. Тогда данную систему можно записать в блочном виде
(3.11)
Здесь 
– векторы размером N каждый. Если их «выстроить подряд», то получится вектор Z. Аналогично, если «выстроить подряд» векторы 
, получится вектор W. Символами 
обозначены блоки матрицы A.
Будем решать систему (3.11) методом исключения по блокам по обычной схеме метода Гаусса. Первое уравнение системы преобразуем к виду
.
Умножая это уравнение на матрицы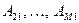 
, и вычитая из последующих 
уравнений, мы получаем систему аналогичного вида, но с неизвестными 
. Так осуществляется один шаг исключения. Совокупность 
шагов исключения образует прямой ход метода Гаусса, а затем обычным образом осуществляется обратный ход.
Вернемся к сеточной системе (3.9). Пусть мы имеем дело с областью
и 
.
Используя граничные условия в наиболее простой форме
,
мы получим для оставшихся 
неизвестных уравнения, которые мы запишем в виде 
групп, причем i -я группа содержит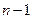 
уравнений, написанных для расчетных точек i -го столбца. При обозначении 
i -я группа уравнений имеет вид
(3.12)
Введем векторы
,
и матрицы
.
Тогда группу уравнений (3.12) можно записать коротко:
. (3.13)
К этому надо добавить, что векторы 
и 
известны.
Мы можем рассматривать систему уравнений (3.13) как результат преобразования к блочному виду системы (3.9). Опишем подробно операции, выполняемые при осуществлении блочного метода Гаусса в применении к системе (3.13). Эта система является блочно-трехдиагональной и этим же свойством обладают промежуточные системы, получаемые при прямом ходе в результате нескольких шагов исключения по Гауссу. Следовательно, если такая промежуточная система связывает векторы 
, то первое уравнение связывает 
. В результате умножения этого уравнения на матрицу, обратную коэффициенту при векторе 
, оно приобретает вид
, (3.14)
где 
– некоторая матрица, а 
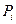– некоторый вектор.
Проделаем еще один шаг исключения, для чего поделим обе части (3.14) 
и вычтем из i -го уравнения (3.13). Это дает
;
.
Теперь ясно, что
. (3.15)
Мы получили рекуррентные соотношения для определения матриц 
и векторов 
. Осталось найти их начальные значения. Если 
, то уравнение (3.13) приобретает вид
,
откуда 
, так что
.
Введем дополнительно матрицу 
и вектор 
. Тогда формулы (3.15) останутся справедливыми и при значении .
Обратный ход заключается в подстановке в формулу 
известного значения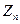 
и дальнейших подстановках 
в формулу (3.14) при значениях 
, 
Наиболее трудоемким при решении системы (3.13) методом блочного исключения является обращение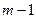 
матриц 
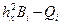размером 
каждая. Это примерно требует 
(c – постоянная величина) операций. Отсюда следует, что если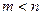 
, то при составлении системы (3.12) следует поменять строки и столбцы местами.
Лемма 3.1.
. (3.16)
Эта лемма показывает, что при проведении блочного исключения по Гауссу в данной системе мы гарантированы от «провалов», возможных в методе Гаусса, – матричные коэффициенты 
, «на которые надо делить», не близки к особенным значениям.
Уравнение колебаний
1. Рассмотрим уравнение
, (4.1)
где 
ищется в той же полуполосе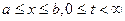 
, что и для уравнения теплопроводности. Функция 
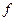считается непрерывной в этой полуполосе.
Рассматриваем первую краевую задачу для уравнения (4.1), т.е. предполагаем, что это уравнение сопровождается граничными условиями
(4.2)
и начальными условиями
(4.3)
Требуем выполнения условий согласования, которые в данном случае выглядят так:
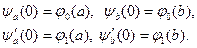
Предполагается существование и единственность решения задачи (4.1) – (4.3), т.е. функции 
, непрерывной в полуполосе 
с производными по переменной x и по переменной t до второго порядка включительно, удовлетворяющей уравнению (4.1) в этой же замкнутой области. Граничные и начальные условия предполагаются выполненными во всех точках (тем самым неявно формулируются дополнительные требования на гладкость функций 
).
Изберем сетку точек 
следующим образом:
,
.
Для численного интегрирования уравнения (4.1) ограничимся рассмотрением одной разностной схемы. Заменим в (4.1) вторые производные по x и по t разностными отношениями с помощью формулы (VI):
, (4.4)
где для погрешности ρ справедлива оценка
(в предположении, что u обладает непрерывными производными до четвертого порядка включительно по x и по t).
Запишем также начальные условия в форме, которая рассчитана на использование приема сдвига сетки на полшага
, (4.5)
. (4.6)
Граничные условия мы сможем удовлетворить точно, без аппроксимации (это справедливо, конечно, только для первой краевой задачи).
При обычных обозначениях можем написать формулу (4.4) для расчетной точки 
:
, (4.7)
а формулы (4.5) и (4.6) – для расчетной точки 
:
, (4.8)
. (4.9)
Отбрасывая остаточные члены, получим из (4.7) – (4.9) систему уравнений
, (4.10)
, (4.11)
. (4.12)
К этим уравнениям добавим запись граничных условий
. (4.13)
Система уравнений (4.10) – (4.13) описывает разностную схему для задачи (4.1) – (4.3). Шаблон для уравнений (4.10) изображен на рис. 4.1.
Ограничиваясь конечным промежутком времени 
, обозначим
.
Рис. 4.1
Обозначим еще через символ m целую часть числа 
.
Будем искать 
для точек , где 
(за исключением точек 
и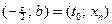 
). Поскольку 
можно найти из (4.13), остаются неизвестными значения 
, а всего 
неизвестных. Для их определения имеются уравнения (4.10), которые можно написать для значений индексов 
, так как для этих значений индексов все точки шаблона лежат в области 
. Всего, таким образом, имеется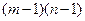 
уравнений (4.10). К ним можно добавить 
уравнений (4.11) и 
уравнений (4.12). Число уравнений оказывается равным числу неизвестных.
Рассматриваемая схема является явной, что следует из вида ее шаблона, в верхнем слое которого расположена всего одна точка. Введя обозначение
,
преобразуем (4.10) к виду
. (4.14)
Формула (4.14) позволяет последовательно «слой за слоем» определить значения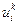 
, если они будут известны для двух начальных слоев. Для определения 
используются формулы (4.11) и (4.12), из которых находим
(4.15)
2. Так же, как и в разделе 1.2., основную роль будет для нас играть вопрос о соотношении шагов h и τ, поскольку общий объем вычислительной работы примерно пропорционален 
.
Мы можем привести по этому поводу соображения, связанные с рассмотрением областей зависимости, совершенно аналогично тому, как это делалось для уравнения теплопроводности.
Скорость распространения возмущений в рассматриваемой задаче (4.1) – (4.3) конечна. Именно, для точки 
(где 
) область зависимости высекается из границы области 
двумя проходящими через эту точку характеристиками уравнения (4.1) и имеет вид, показанный на рис. 4.2, а) жирными линиями. При этом 
. Для сеточной схемы область зависимости имеет такой же вид (рис. 4.2, б)), но при этом 
. Как показано в 1.2, область зависимости для задачи (4.1) – (4.3) должна содержаться в области зависимости для сеточной задачи. Иными словами, должно быть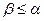 
, т.е. 
.
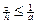Таким образом, ясно, что необходимо принять
. (4.16)
а) б)
Рис. 4.2
Другое соображение для выбора соотношения шагов заключается в сравнении порядка аппроксимации разностным отношением отдельных членов дифференциального уравнения. Остаточный член при аппроксимации левой части дифференциального уравнения имеет порядок 
, а при аппроксимации правой части – порядок 
. Естественно выбирать h и τ величинами одного порядка малости, т.е. сделать c величиной, ограниченной снизу и сверху положительными постоянными.