Метод изучения устойчивости разностных схем, носящий название метода гармоник, основан на использовании аналогичных представлений для дискретного случая. Об устойчивости схемы, т.е. об эволюции во времени полученного с помощью этой схемы разностного решения, судят по поведению частных сеточных решений, имеющих вид разностной гармоники.
Итак, рассмотрим частное решение задачи (2.1), имеющее вид
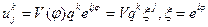, (2.39)
где i – мнимая единица 
, q – комплексное число, подлежащее определению, φ – произвольное вещественное число, j, k – пространственный номер и временной номер узла сетки. Для простоты можно считать 
. Тогда
. (2.40)
Величина q подбирается так, чтобы гармоника (2.40) действительно была решением, т.е. удовлетворяла разностному уравнению.
Заметим, что 
и 
. В то же время величина 
может принимать любое значение (положительное). Если окажется, что для некоторых φ 
, то соответствующие гармоники во времени будут неограниченно нарастать. Это означает нарушение неравенства
и свидетельствует о неустойчивости схемы на решениях частного вида. Неустойчивость схемы в частном случае порождает неустойчивость в общем случае, - ведь общее решение может содержать «неустойчивую гармонику» с величиной .
Если при любых значениях φ имеем 
, то все гармоники (2.40) ограничены. Однако отсюда еще не следует ограниченность общего решения. Поэтому условие представляет достаточное условие неустойчивости, а – необходимое условие устойчивости. Метод гармоник позволяет устанавливать неустойчивость схемы.
Проверим методом гармоник устойчивость явной разностной схемы (вариант 1)
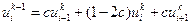, (2.9)
где
.
Подставляя (2.40) в (2.9), получим
.
Имеем, что схема неустойчива, если
.
И схема устойчива, если
.
Проверим методом гармоник устойчивость неявной разностной схемы (вариант 2)
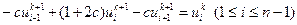. (2.13)
Подставляя (2.40) в (2.13), получим
.
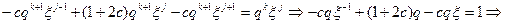
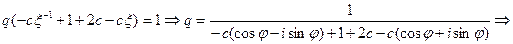
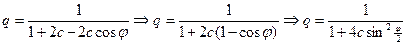И схема устойчива, т.к. 
.
Дополнение. Вариант 3.
2. Применяя формулу (IX) для аппроксимации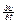 
разностными отношениями и формулу (VI) для аппроксимации 
, напишем разностный аналог уравнения (2.1).
3. 
(2.41)
Для остаточного члена 
справедлива оценка
.
Вводя обозначения 
, напишем соотношение (2.41) для расчетной точки 
:
. (2.42)
Отбрасывая остаточный член, получаем искомое разностное уравнение:
. (2.43)
Рассматриваемому варианту 3 отвечает следующий шаблон (рис. 2.6), в котором кружком с крестиком обозначена расчетная точка.
Шаблон варианта 3 является пятиточечным трехслойным.
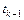
Рис. 2.6
4. Пусть m есть целая часть отношения 
. Из начальных и граничных условий находим
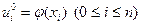, (2.7)
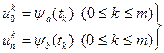. (2.8)
В силу условий согласования равенства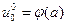 
и 
, а также 
и 
совместны.
5. Учитывая (2.7), (2.8), разностная схема (2.6) имеет 
неизвестных значений
.
Подсчитаем количество имеющихся в нашем распоряжении уравнений для варианта 3. При этом следует позаботиться, чтобы в уравнения не входили новые неизвестные, т.е. чтобы все узлы сетки, принадлежащие шаблону, не выходили за пределы 
.
Уравнения (2.42) пишем для значений 
, так что число уравнений на 
меньше числа неизвестных и потому к уравнениям (2.42) следует добавить еще уравнений. Это можно сделать по-разному. Мы прибегнем к аппроксимации производной 
с помощью несимметричного разностного отношения (IV), остаточный член которого имеет второй порядок, подобно остаточному члену в (2.42):
,
где
.
Полагая здесь 
и отбрасывая остаточные члены, получаем
. (2.44)
Эти уравнения мы присоединим к (2.42), в результате чего получаем систему уравнений, число которых равно числу неизвестных.
Рассмотрим вопрос о том, как решать системы линейных алгебраических уравнений, получившихся в варианте 3. Допустим, что получено сечение 
, и поставим вопрос о продолжении счета на слои 
. В трехслойном шаблоне варианта 3 в верхнем слое имеется лишь одна точка. Поэтому в этом варианте (как и в варианте 1) из формул (2.42) получается рекуррентная зависимость
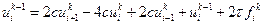(2.45)
и мы можем слой за слоем определить 
(с использованием граничных условий). Схема варианта 3 является, как и схема варианта 1, явной.
Что касается определения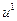 
, мы используем уравнения (2.43). Исключим 
при помощи группы уравнений (2.42), соответствующих 
. Запишем для этого те и другие уравнения в форме
,
откуда
. (2.46)
Таким образом, определение первого сечения 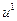осуществляется неявным образом.
6. Перейдем к исследованию варианта 3. Из исследований варианта 1 вытекает, что при использовании явной схемы следует отношение 
стремить к нулю. Разумеется, это полностью относится и к варианту 3.
В варианте 3 левая часть уравнения (2.1) аппроксимируется с погрешностью порядка 
, а правая – с погрешностью порядка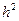 
. Здесь целесообразно выбирать τ и h величинами одного порядка малости.
Можно показать методом гармоник, что при любом c процесс нахождения приближенных решений оказывается неустойчивым.
Вариант 3 оказывается непригодным к вычислениям. Это позволяет нам отказаться от дальнейшего исследования этого варианта.
Дополнение. Вариант 4.
2. Четвертый вариант записи уравнения (2.1) в разностной форме получается несколько сложнее. Напишем сначала
, (2.47)
где
(линейная интерполяция функции по переменной t на середину промежутка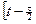 
; 
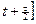по значениям в его концах). Теперь запишем уравнение (2.1), аппроксимируя производную по времени с помощью формулы (IX) при шаге 
, а производные по переменной x, входящие в правую часть (2.47), – по формуле (VI).
3. Это дает
, (2.48)
где для погрешности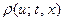 
с учетом (2.47) и оценки 
получаем
. (2.49)
Вводя обозначения , напишем соотношение (2.48) для расчетной точки 
. Тогда 
. Это приводит к уравнению
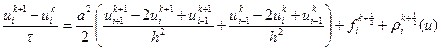. (2.50)
Отбрасывая остаточный член, получаем искомое разностное уравнение
. (2.51)
Указанному варианту 4 отвечает следующий шаблон (рис. 2.7). Обратим внимание на то, что в варианте 4расчетная точка не принадлежит сетке.
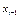
Рис. 2.7
Шаблон варианта 4 является шеститочечным двухслойным.
4. Пусть m есть целая часть отношения . Из начальных и граничных условий находим
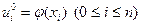, (2.7)
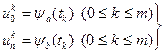. (2.8)
В силу условий согласования равенства 
и , а также 
и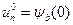 
совместны.
5. В варианте 4 мы, как и в варианте 1, можем написать уравнение (2.51) для значений индексов 
, и число уравнений равно числу неизвестных.
Двухслойный шаблон варианта 4 содержит в верхнем слое три точки, и поэтому мы имеем на этот раз дело с неявной схемой. Формулы (2.51) преобразуются к виду
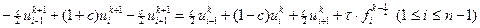. (2.52)
Переход от k -го слоя к 
слою требует решения системы (2.52) с трехдиагональной матрицей (при использовании граничных условий). Зная сечение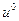 
, мы можем последовательно определить сечения 
.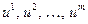