Перейдем теперь к выяснению основного вопроса – будет ли полученное численным методом решение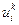 
близко к точному решению исходной задачи 
. Очевидно, надеяться на это можно лишь при малых значениях τ и h.
Понятие корректности разностной задачи определяют аналогично определению корректности применительно к задачам математической физики.
Пусть 
– решение, а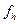 
– входные данные некоторой разностной задачи. Они зависят от параметра h. Меняя h, мы получаем последовательности решений 
и входных данных 
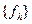. Таким образом, мы рассматриваем не одну разностную задачу, а семейство задач, зависящее от параметра h. Понятие корректности вводится для семейства разностных задач (схем), если 
.
Будем говорить, что разностная задача (схема) корректна, если при всех достаточно малых значениях 
:
1) решение разностной задачи существует и единственно для всех входных данных 
из некоторого допустимого семейства;
2) решение непрерывно зависит от входных данных 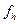, причем эта зависимость равномерна относительно h.
Более того, второе условие означает, что существует такая постоянная величина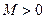 
, не зависящая от h, что при достаточно малом значении 
выполняется неравенство
, (2.24)
где 
– решение задачи с входными данными 
.
Свойство непрерывной зависимости решения разностной задачи от входных данных, выраженное неравенством (2.24), называется устойчивостью схемы по входным данным или просто устойчивостью.
В разделе 1.2.1 было введено определение сходимости разностной схемы. Исследование сходимости разностной схемы проводят в два этапа:
1) устанавливают аппроксимацию задачи (1.1) разностной схемой (1.2);
2) проверяют устойчивость разностной схемы.
Говорят, что разностная схема (1.2) аппроксимирует задачу (1.1), если
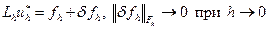, (2.25)
величину 
называют погрешностью аппроксимации.
Если 
, то говорят, что разностная схема (1.2) аппроксимирует задачу (1.1) на решении 
с порядком s относительно h.
Для линейного оператора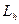 
определение (2.24) равносильно следующему определению.
Разностная схема (1.2) называется устойчивой, если существует такое 
, что при всех 
и любых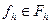 
:
1) разностная схема (1.2) имеет единственное решение;
2) 
, где K – постоянная величина относительно h и .
Если разностная схема (1.2) аппроксимирует задачу (1.1) с порядком s относительно h и устойчива, то будет выполняться (2.25), если 
.
Перейдем к исследованию рассмотренных вариантов. Цель этого исследования - нахождение условий сходимости и устойчивости.
Как следует из рассмотренных вариантов, объем вычислений для каждого варианта примерно пропорционален числу узлов 
в области 
(коэффициент пропорциональности, конечно, зависит от варианта). В связи с этим основную роль во всех рассмотрениях играет вопрос о количестве узлов, которое нужно избрать, чтобы обеспечить необходимую точность. Эти рассмотрения мы будем вести довольно грубо. Именно, будем предполагать, что 
, и оценивать, с какой скоростью нужно при этом стремить к нулю τ. Тем самым определится порядок стремления к бесконечности числа узлов, пропорционального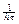 
.
В рассматриваемой задаче (2.1) – (2.3) имеет место бесконечная скорость распространения возмущений. Это значит, что для заданного уравнения (2.1) и для любой точки 
изменение функции 
на промежутке 
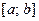и функций 
и 
на промежутке 
повлечет, вообще говоря, изменение значения 
(хотя бы 
было сколь угодно близко к нулю, а изменение 
происходило при значениях x, далеких от значения 
).
Иначе говоря, «область зависимости» на границе 
для исходно задачи (2.1) – (2.3) такова, как показано на рис. 2.5, а) жирной линией.
Для сеточной задачи при явной схеме варианта 1 дело обстоит иначе. Пусть есть точка сетки
.
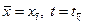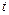
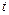
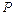
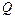
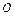
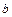
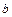
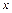
Рис. 2.5, а) Рис. 2.5, б)
Как ясно из рассмотрения соответствующего шаблона, значение 
выражается через правую часть уравнения (2.1) и через значения 
лишь в трех точках 
слоя
,
т.е. через отрезок длиной 
. В свою очередь для вычисления этих трех значений нам понадобятся значения лишь в пяти точках 
слоя
.
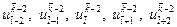Тогда решение выражается через отрезок нулевого слоя длиной
;
этот отрезок будет областью зависимости.
Если мы проведем через точку M с координатами 
лучи MP и MQ, образующие с осью x углы 
, то при вычислении 
будут использованы значения лишь в той части сеточной области 
, которая лежит в угле PMQ. В частности, зависит от граничных и начальных сеточных значений сеточной функции (а, следовательно, и функции u) лишь на части границы 
, лежащей в этом угле. Иначе говоря, область зависимости такова, как показано жирной линией на рис. 2.5, б).
Скорость распространения возмущений в сеточной задаче оказывается конечной. Это значит, что изменение значений 
на участке границы вне области зависимости, показанной на рис. 2.5, б), не скажется на значении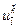 
.
Устремим h и τ к нулю, сохраняя отношение 
постоянной величиной, так чтобы точка была узлом сетки при всех рассматриваемых h и τ. Для точного решения область зависимости бесконечна. Значит сходимость к точному решению, если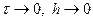 
возможна, только если дополнительно 
, т.е. 
Тогда будет иметь место парадоксальное положение вещей, когда, изменяя начальные или граничные условия на тех участках границы, которые на рис. 2.5, а) показаны жирной линией, а на рис. 2.5, б) тонкой линией, мы могли бы изменить , не меняя при этом значение 
в точке .
Ясно, что при этом рассчитывать на сходимость сеточной функции к точной функции 
в точке не было бы никаких оснований.
Эти соображения показывают, что при использовании явной схемы варианта 1 следует отношение стремить к нулю.
Для неявной схемы варианта 2 эти соображения теряют силу, ибо независимо от параметра h область зависимости для точки 
состоит из всех точек границы до 
слоя включительно и эта область совпадает с областью зависимости, изображенной на рис. 2.5, а). Действительно, для нахождения следует решить систему уравнений, в которой связаны значения 
во всех узлах сетки до слоя включительно (кроме узлов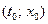 
и 
для варианта 2).
Приведем некоторые другие соображения. В вариантах 1 и 2 остаточный член при замене дифференциального уравнения разностным уравнением состоит из двух слагаемых. Первое получается в результате замены разностным отношением левой части уравнения (2.1) и имеет порядок τ, второе – в результате замены разностным отношением правой части и имеет порядок 
.
Естественно при значении придать величине τ порядок , иначе была бы несогласованность в точности аппроксимации производных по переменной t и по переменной x - большая точность аппроксимации одной из них не была бы использована.
Подчеркнем следующий существенный факт. Разностная задача (2.6) аппроксимирует исходную дифференциальную задачу (2.1) – (2.3) вне зависимости от того, выполнены или нет условия (1.8). Однако оказывается, что одной аппроксимации недостаточно для сходимости 
к точному решению . Дополнительным условием, обеспечивающим сходимость, является в данной задаче . Невыполнение их может привести к любому отклонению сеточной функции от точной функции .
Перейдем теперь к выяснению основного вопроса – будет ли полученное численным методом решение 
близко к точному решению исходной задачи 
. Очевидно, надеяться можно на это лишь при малых значениях 
.
Положим
(2.26)
и подставим это выражение в разностную формулу (2.6)
. (2.6)
Получим
. (2.27)
Здесь и далее 
означает 
. Оценим правую часть (2.27). Считая 
гладкой функцией при малых значениях τ и h, имеем
.
Так как удовлетворяет уравнению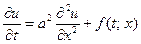 
, а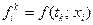 
, то последнее равенство означает, что
. (2.28)
Сравнивая (2.28) с (2.6), заключаем, что решение исходной задачи удовлетворяет разностное уравнение (2.6) с точностью 
, т.е. аппроксимация имеет место.
Подставляя (2.28) в правую часть (2.27), получим уравнение для определения 
(невязки):
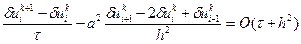(2.29)
или
. (2.30)
Сначала рассмотрим случай, когда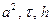 
удовлетворяют неравенствам
. (2.31)
В этом случае коэффициенты при величинах 
в правой части (2.30) положительны, и можно написать
.
Введем обозначение
, (2.32)
тогда предыдущее неравенство дает
, (2.33)
т.е. максимальное отклонение 
за один шаг τ увеличивается не более чем на величину 
. Соответственно за m шагов это даст
. (2.34)
Зафиксируем любое конечное 
и устремим к нулю, а m соответственно к бесконечности.
Поскольку 
, то из (2.34) следует
. (2.35)
Итак, мы доказали, что если при стремлении к нулю условия (2.31) выполнены, то решение разностной задачи варианта 1сходится к решению исходной задачи (2.1).
Исследование устойчивости по ε схеме
Рассмотрим теперь противоположный случай, когда стремление 
к нулю проходит таким образом, что хотя бы одно из условий (2.31) нарушено. Оказывается, что в этом случае сходимости, вообще говоря, нет. Покажем это с помощью следующего простого рассуждения. Обратимся к формуле (2.30), которая описывает процесс эволюции ошибки от слоя к слою. Наличие в правой части члена 
указывает на то, что порядок ошибки, во всяком случае, не меньше этой величины. Сама ошибка 
есть некоторая сложная функция от индекса i. Допустим, что ее можно представить в виде суммы, одно из слагаемых которой имеет вид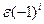 
, где разумеется, 
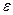имеет порядок . Проследим за развитием только этой компоненты ошибки, т.е. положим
, (2.36)
и найдем 
При этом, несколько идеализируя задачу, не будем учитывать вклад, даваемый членом на следующих шагах. Получим
,
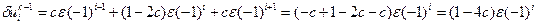т.е. функция вида (2.36) переходит на следующем слое в себя, приобретая множитель 
. Очевидно, через m слоев она приобретает множитель 
:
, (2.37)
и, следовательно, развитие рассматриваемой компоненты ошибки определяется величиной . Если
, (2.38)
то ошибка затухает, в противном случае нарастает экспоненциально.
Последнее приводит к тому, что решение 
, содержащее эту ошибку, довольно быстро теряет какой-либо смысл, становясь хаотической последовательностью очень больших чисел. Малое значение ε, очевидно, не спасает положения и может лишь несколько оттянуть наступление катастрофы. Описанный эффект получил название неустойчивости.
Нетрудно заметить, что (2.38) есть опять все то же условие (2.31). А это значит, что отсутствие сходимости и неустойчивость имею одну и ту же причину. Используя (2.37) для конечного отрезка , получаем, что в случае нарушения условия (2.37), т.е. (2.31)
.
Расчет по неустойчивой разностной схеме не только не дает решения, близкого к точному решению, но вообще невозможен. При этом уменьшение только ухудшает положение.