«Прямолинейное равноускоренное движение»
Вариант № 1
1.Какую скорость будет иметь тело через 20 сот начала движения, если оно движется с ускорением 0,2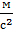 
.
2.Зависимость проекции скорости от времени движущегося тела задана уравнением υх = 1 + 2 t. Опишите это движение (укажите значения характеризующих его величин), постройте график υx = υx(t).
3.По наклонной доске пустили катиться снизу вверх шарик. На расстоянии 30 см от начала пути шарик побывал дважды: через 1 с и через 2 с после начала движения. Определите начальную скорость и ускорение движения шарика. Ускорение считать постоянным.
Вариант № 2
1.Через 25 с после начала движения спидометр автомобиля показал скорость движения 36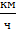 
. С каким ускорением двигался автомобиль?
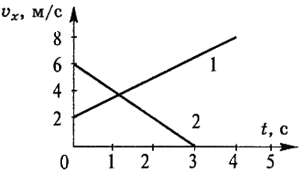
2По графикам, изображённым на рисунке, записать уравнения зависимости проекции скорости и координаты тела от времени υx = υx(t) и х = х(t).
3.При равноускоренном движении точка проходит в первые два равных последовательных промежутка времени, по 4 с каждый, пути 24 м и 64 м. Определить начальную скорость и ускорение движущейся точки.
Вариант № 3
1.За 5 с скорость шарика возросло с 2 
до 5 . Определить ускорение шарика.
2.Уравнение движения тела sх = 2 t + t2. Опишите это движение (укажите значения характеризующих его величин). Постройте график sx = sx(t).
3.Первый вагон поезда прошёл мимо наблюдателя, стоящего на платформе, за 1 с, а второй – за 1,5 с. Длина вагона 12 м. Найти ускорение поезда и его скорость в начале наблюдения. Движение поезда считайте равноускоренным.
Вариант № 4
1.За какое время автомобиль, двигаясь с ускорением 0,2 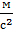, уменьшит свою скорость на 10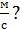 
2.По графикам, изображённым на рисунке, записать уравнения зависимости проекции скорости и координаты тела от времени υx = υx(t) и х = х(t).
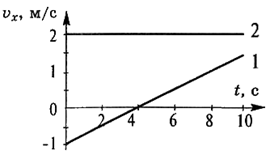
3.Тележка двигалась вдоль наклонной плоскости с постоянным ускорением. В момент, когда секундомер показывал 7 с, тележка находилась против отметки 70 см, в момент времени 9 с – против отметки 80 см и при 15 с – против отметки 230 см. С каким ускорением двигалась тележка?
Вариант № 5
1.Велосипедист движется под уклон с ускорением 0,2 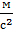. Какую скорость приобретает велосипедист через 10 с, если его начальная скорость равна 5 ?
2.Зависимость проекции скорости от времени движущегося тела задана уравнением υх = 4 + t. Опишите это движение (укажите значения характеризующих его величин), постройте график υx = υx(t).
3.За какую секунду от начала движения путь, пройденный телом при равноускоренном движении, втрое больше пути, пройденного в предыдущую секунду, если движение происходит без начальной скорости?
Вариант № 6
1.Какое перемещение пройдёт тело за 5 с, если его ускорение 2 ?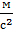
2.По графикам, изображённым на рисунке, записать уравнения зависимости проекции скорости и координаты тела от времени υx = υx(t) и х = х(t).
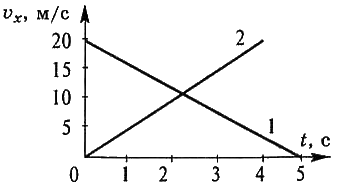
3. Два поезда прошли одинаковый путь за одно и то же время, однако один поезд, имея начальную скорость, равную нулю, прошёл весь путь с ускорением 3 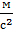, а другой поезд половину пути шёл со скоростью 18 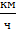, а другую половину пути со скоростью 54 
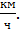Найти путь, пройденный поездами.
Вариант № 7
1.Велосипедист, движущийся со скоростью 3 , начинает спускаться с горы с ускорением 0,8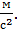 
Найдите длину горы, если спуск занял 6 с.
2.Уравнение движения тела sх = 6 – t2. Опишите это движение (укажите значения характеризующих его величин). Постройте график sx = sx(t).
3.Наклонная плоскость длиной l разделена на три участка. Каковы длины этих участков, если скатывающийся по наклонной плоскости шарик проходит эти участки за одинаковое время?
Вариант № 8
1.За какое время автомобиль, двигаясь из состояния покоя с ускорением 0,6 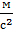, пройдёт путь 30 м?
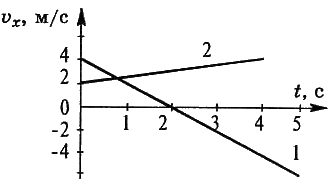
2.По графикам, изображённым на рисунке, записать уравнения зависимости проекции скорости и координаты тела от времени υx = υx(t) и х = х(t).
3. В момент, когда опоздавший пассажир вбежал на платформу, с ним поравнялось начало предпоследнего вагона, который прошёл мимо него за время t1. Последний вагон прошёл мимо пассажира за время t2. На сколько опоздал пассажир к отходу поезда? Поезд движется равноускоренно. Длина вагонов одинакова.