Тема: Средние величины
Введение: Характеристика цели занятия, закрепление теоретических знаний об абсолютных, относительных и средних величинах; выработка практические навыки их исчисления.
Вопросы для обсуждения:
· Виды и значение обобщающих показателей.
· Виды абсолютных величин.
· Виды и взаимосвязь относительных величин.
Задача № 1.
Имеются следующие данные о заработной плате рабочих-сдельщиков.
Таблица 1
| Месячная заработная плата, грн. (варианта х) | Число рабочих (f) | x · f |
 = 1000
| ||
 = 1200
| ||
 = 1500
| ||
 = 1700
| ||
 = 2000
| ||
| Итого |
Определите среднюю заработную плату одного рабочего.
Ход решения:
Данные представлены в виде дискретного ряда распределения, по которому видно, что одни и те же значения признака (варианты) повторяются несколько раз. Так, варианта встречается в совокупности 2 раза, а варианта 
– 16 раз и т.д.
Исчислим среднюю заработную плату одного рабочего (
):
Средняя заработная плата 1-го рабочего = 
Средняя з/п 1-го рабочего =
Задача № 2.
Имеются следующие данные о выполнении норм выработки рабочими.
Таблица 2
| Группа рабочих по выполнению норм выработки, % (х) | Число рабочих, % к итогу (f) | Накопленные частоты, %, 
|
| 90-100 | ||
| 100-110 | ||
| 110-120 | ||
| 120-130 | ||
| Итого |
Определите моду и медиану.
Ход решения:
1. Определим моду: 
;
.
2.Определим медиану:
Вывод: мода равна 104,2%, медиана равна 104,58%.
Задача № 3.
На протяжении недели два акционерных банка, которые продавали акции по цене 2,0 и 3,0 грн. за одну, получили одинаковую выручку: по 1200 грн. Определить среднюю цену акции.
Ход решения:
Средняя цена акции определяется делением общей выручки двух банков (2400) на общее количество проданных акций (1000 шт.), вычисленную делением выручки каждого банка на цену акции: (1200/2) + (1200/3).
Расчёт можно представить в виде формулы:
,
где 
- цена акций; 
- выручка от реализации.
грн.
Поскольку выручка от реализации акций в двух банках одинакова (
), то эту величину можно вынести за скобки в числителе и знаменателе и сократить:
грн.
Задача № 4.
Введение в действие жилья населением за свой счёт характеризуется следующими коэффициентами снижения (относительно предыдущего года):
Таблица 1
| Год | |||
| Коэффициент | 0,93 | 0,81 | 0,99 |
Определить среднегодовой коэффициент снижения объемов введённого в действие жилья населением за свой счёт за 2008-2010 гг.
Ход решения:
Ряд динамики представлен в виде коэффициентов снижения, рассчитанных цепным способом (по отношению к предыдущему году). Средний коэффициент снижения в этом случае будет рассчитан по формуле средней геометрической взвешенной:
.
Задача № 5.
Урожайность и валовой сбор ячменя бригадами совхоза «Заря» характеризуется следующими данными: Определить среднюю урожайность ячменя по совхозу.
Таблица 1
| Номер бригады | Урожайность, ц/га | Валовой сбор, ц |
| №1 | 22,0 | |
| №2 | 23,0 | |
| №3 | 22,5 |
Определить среднюю урожайность ячменя по совхозу.
Ход решения:
В качестве изучаемого признака, который необходимо осреднить, выступают показатели урожайности ячменя по трём бригадам. А валовой сбор ячменя – это произведение урожайности в соответствующих бригадах на их частоты (посевные площади). Поэтому необходимо использовать среднюю гармоническую взвешенную.
.
Средняя урожайность ячменя по совхозу «Заря» составила в отчётном периоде 22,5 ц/га.
Задача № 6.
Бригада упаковщиков цеха упаковки шоколадной фабрики из трёх человек должна собрать 1040 коробок конфет «Ассорти». Первый упаковщик тратит на формирование 1 коробки 4 минуты, второй – 3 минуты, третий – 2 минуты. Определить, сколько времени потребуется бригаде на формирование заказа.
Ход решения:
Общие затраты времени на выполнение задания:
,
где 
- средняя трудоёмкость формирования одной коробки конфет;
- объём заказа в натуральном выражении.
Среднюю трудоёмкость определяем по формуле средней гармонической простой:
Тогда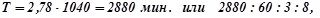 
то есть бригаде потребуется 2 полных 8 - часовых рабочих дня. (делим на 60, т.к. в 1ч 60 мин, делим на 3, т. к. 3 человека в бригаде, делим на 8 – 8-мичасовой рабочий день).
Задача № 7.
Четыре швеи-надомницы заняты пошивом головных уборов одной модели. Первая швея тратит на изготовление 1 убора 30 минут, 2-я – 40, 3-я – 50, 4-я – 60 мин. Определить средние затраты времени на пошив 1 головного убора при условии, что каждая швея работает по 10 часов в день.
Ход решения:
Использовать формулу средней арифметической нельзя, так как каждая швея шьёт не по 1 убору в день. Количество уборов, сшитых каждой швеёй:
1. 600: 30 = 20 шт
2. 600: 40 = 15 шт.
3. 600: 50 = 12 шт.
4. 600: 60 = 10 шт.
Используем формулу средней гармонической взвешенной:
мин.
Задача № 8.
На основании следующих данных по двум сельскохозяйственным предприятиям необходимо определить, в каком из них и насколько выше средняя урожайность зерновых культур.
Таблица 1
| Культура | Предприятие №1 | Предприятие №2 | ||
| Валовой сбор, ц | Урожайность, ц/га | Посевная площадь, га | Урожайность, ц/га | |
| Пшеница | 32 500 | 1 540 | ||
| Рожь | 1 620 | |||
| Ячмень | 13 640 | |||
| Просо | 1 650 | |||
| Итого | 49 410 | - | 1 900 | - |
Ход решения:
Урожайность является вторичным признаком, так как она задана на единицу первичного признака (посевной площади, выраженной абсолютной величиной) и может быть представлена как отношение двух первичных признаков, а именно, валового сбора и посевной площади:
.
Следовательно, для расчёта средней урожайности необходимо применить среднюю взвешенную, но какую: арифметическую или гармоническую? Согласно правилу № 2 (см. три правила выбора средней: если в указанной постановке задачи известны численные значения числителя логической формулы, а значения знаменателя не известны, но могут быть найдены как частное от деления одного показателя на другой, то средняя вычисляется по формуле средней гармонической) для предприятия № 1 использую формулу средней гармонической взвешенной:
.
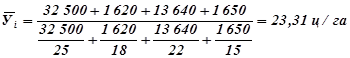
Для предприятия №2 средняя урожайность определяется по правилу №1: Если имеется ряд данных по двум взаимосвязанным показателям, для одного из которых нужно вычислить среднюю величину, и при этом известны численные значения знаменателя её логической формулы, а значения числителя не известны, но могут быть найдены как произведения этих показателей, то средняя должна находиться по формуле средней арифметической взвешенной:
.
Вывод: Средняя урожайность на предприятии №1 по сравнению с предприятием №2 выше на 4,04 ц/га (или на 
, то есть на 21 %).
Задача № 9.
Имеем два квадрата со сторонами 20 и 39 см. Определить сторону квадрата, площадь которого является средней арифметической площадей этих квадратов.
Ход решения:
Площадь 1-го квадрата:
;
Площадь 2-го квадрата:
;
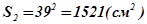Находим среднюю арифметическую из этих площадей, т. е. площадь нового 3-го квадрата:
.
Находим сторону:
.
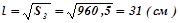Задача № 10.
Имеются следующие данные о заработной плате заведующих секцией в магазине.
Таблица 1.
| Месячная зарплата (грн.). (Х.). | Число заведующих секцией |
Определите среднюю заработною плату одного заведующего секцией.
Решение:
1. Определяем среднюю зарплату одного зав. секцией по формуле средней арифметической взвешенной:
Ответ: средняя зарплата одного заведующего секцией составила 350 грн.
Задача № 11.
Имеются следующие данные о производительности труда продавцов за год.
Таблица № 4.
| Количество обслуживаемых покупателей за час (чел.) | Число продавцов (чел.) |
| 6 – 8 | |
| 8 – 10 | |
| 10 – 12 | |
| 12 – 14 |
Определите среднее количество обслуживаемых покупателей за час одним продавцом.
Решение:
1. Определим середину интервала для каждой группы по формуле средней арифметической простой:
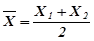
Так, для первой группы дискретная величина 
будет равна:
Расчеты представим в табличной форме:
Таблица № 5.
| Количество обслуживаемых покупателей за час (чел.) (Х). | Число продавцов (f) | Середина интервала
( )
| ( )
|
| 6-8 | |||
| 8-10 | |||
| 10-12 | |||
| 12-14 | |||
| Итого: | - |
3. Определим среднее количество обслуживаемых покупателей по формуле средней арифметической взвешенной:
Ответ: Все продавцы обслужили за час 248 человек, а каждый в среднем обслужил по 9,5 человек.