Диаграммы предельных амплитуд и предельных напряжений.

При эксплуатации машин и инженерных сооружений в их эле­ментах возникают напряжения, изменяющиеся во времени по самым разнообразным циклам. Для расчета элементов на прочность необходимо иметь данные о величинах пределов выносливости при циклах с различными коэффициентами асимметрии. Поэтому наряду с испытаниями при симметричных циклах испытания проводят и при асимметричных циклах.

Следует иметь в виду, что испытания на выносливость при асимметричных циклах выполняют на специальных машинах, конст­рукции которых значительно сложнее, чем конструкции машин для испытания образцов при симметричном цикле изгиба.

Результаты испытаний на выносливость при циклах с различ­ными коэффициентами асимметрии обычно представляют в виде диаграмм (графиков), изображающих зависимость между какими-либо двумя параметрами предельных циклов.Эти диаграммы можно построить, например, в координатах , ,их называют диаграм­мами предельных амплитуд,они показывают зависимость между средними напряжениями и амплитудами предельных циклов, для которых максимальные напряжения равны пределам вынос­ливости: . Здесь и ниже максимальное, минимальное, сред­нее и амплитудное напряжения предельного цикла будем обозна­чать .

Диаграмму зависимости между параметрами предельного цикла можно построить также в координатах .Такую диаграмму называют диаграммой предельных напряжений.

При расчете стальных конструкций в промышленном и граж­данском строительстве применяют диаграммы, дающие зависимость между коэффициентом асимметрии цикла и пределом выносли­вости .

Подробно рассмотрим диаграмму предельных амплитуд (её иногда называют диаграммой ), которая в дальнейшем исполь­зована для получения зависимостей, применяемых в расчетах на прочность при переменных напряжениях.

Для получения одной точки рассматриваемой диаграммы необходимо испытать серию одинаковых образцов (не менее 10 штук) и построить кривую Вёлера, по которой определится величина предела выносливости для цикла с данным коэффициентом асим­метрии (это относится и ко всем другим типам диаграмм для пре­дельных циклов).

Допустим, проведены испытания при симметричном цикле изгиба; в результате получена величина предела выносливости . Координаты точки, изображающей этот предельный цикл, равны: [см. формулы (1-15) — (3.15)], т. е, точка находится на оси ординат (точка на рис. 6.15). Для произволь­ного асимметричного цикла по пределу выносливости , определенному из опытов, нетрудно найти . По фор­муле (3.15),

но [см. формулу (5.15)], следовательно,

или

(7.15)

и

(8.15)

В частности, для отнулевого цикла при пределе выносливости, разном .

Этому циклу соответствует точка на диаграмме, представ­ленной на рис. 6.15. Определив экспериментальное значение для пяти-шести различных циклов, по формулам (7.15) и (8.15) получают координаты , и отдельных точек, принадлежащих предельной кривой. Кроме того, в результате испытания при по­стоянной нагрузке определяют предел прочности материала, кото­рый для общности рассуждений можно рассматривать как предел выносливости для цикла с 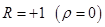, т. е. . Этому циклу на диаграмме соответствует точка В. Соединяя плавной кривой точки, координаты которых найдены по экспериментальным данным, получают диаграмму предельных амплитуд (рис. 6.15),

Рис. 6.15

Рассуждения о построении диаграммы, проведенные для циклов нормальных напряжений, применимы для циклов касательных на­пряжений (при кручении), но изменяются обозначения ( вместо и т. п.).

Диаграмма, представленная на рис. 6.15, построена для цик­лов с положительными (растягивающими) средними напряжениями . Конечно, принципиально возможно построение подобной диаграммы и в области отрицательных (сжимающих) средних напря­жений , но практически в настоящее время имеется весьма немного опытных данных об усталостной прочности при . Для мало- и среднеуглеродистых сталей приближенно можно при­нимать, что в области отрицательных средних напряжений пре­дельная кривая параллельна оси абсцисс.

Рассмотрим теперь вопрос об использовании построенной диа­граммы. Пусть рабочему циклу напряжений соответствует точка с координатами (т. е. при работе в рассматриваемой точке детали возникают напряжения, цикл изменения которых задан какими-либо двумя параметрами, что позволяет найти все параметры цикла и, в частност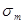и, и ).

Проведем из начала координат луч через точку N. Тангенс угла наклона этого луча к оси абсцисс равен характеристике цикла:

Очевидно, что любая другая точка, лежащая в том же луче, соответствует циклу, подобному заданному (циклу, имеющему те же значения и ). Итак, любой луч, проведенный через начало координат, является геометрическим местом точек, соответ­ствующих подобным циклам. Все циклы, изображаемые точками луча, лежащими не выше предельной кривой (т.е. точками от­резка ОК), безопасны в отношении усталостного раз­рушения. При этом цикл, изображаемый точкой К, является для заданного коэффициента асимметрии предельным – его макси­мальное напряжение, определяемое как сумма абсциссы и орди­наты точки К (), равно пределу выносливости:

Аналогично для заданного цикла максимальное напряжение равно сумме абсциссы и ординаты точки N:

Считая, что рабочий цикл напряжений в рассчитываемой детали и предельный цикл подобны, определяем коэффициент запаса проч­ности как отношение предела выносливости к максимальному на­пряжению заданного цикла:

Как следует из изложенного, коэффициент запаса при наличии диаграммы предельных амплитуд, построенной по эксперименталь­ным данным, можно определить графоаналитическим способом. Однако такой способ пригоден лишь при условии, что рассчиты­ваемая деталь и образцы, в результате испытаний которых полу­чена диаграмма, идентичны по форме, размерам и качеству обработки.

Для деталей из пластичных материалов опасно не только уста­лостное разрушение, но и возникновение заметных остаточных дефор­маций, т. е. наступление текучести. Поэтому из области, ограни­ченной линией АВ (рис. 7.15), все точки которой соответствуют циклам, безопасным в отношении усталостного разрушения, надо выделить зону, соответствующую циклам с максимальными напря­жениями, меньшими предела текучести. Для этого из точки L, абсцисса которой равна пределу текучести о_т, проводят прямую, наклоненную к оси абсцисс под углом 45°. Эта прямая отсчет на оси ординат отрезок ОМ, равный (в масштабе диаграммы) пределу текучести. Следовательно, уравнение прямой LM (уравнение в от­резках) будет иметь вид

или

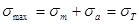
т. е. для любого цикла, изображаемого точками линии LM, мак­симальное напряжение равно пределу текучести. Точки, лежащие выше линии LM, соответствуют циклам с максимальными напря­жениями, большими предела текучести (). Таким образом, циклы, безопасные как в отношении усталостного разрушения, так и в отношении возникновения текучести, изображаются точками области OADL,.

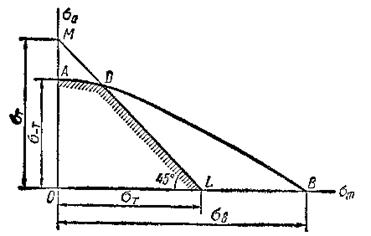
Рис. 7.15

Довольно широко применяется также диаграмма предельных напряжений, изображающая зависимость предельных значений максимальных и минимальных напряжений циклов от предельных средних напряжений (так называемая диаграмма Смита). Примерный вид такой диаграммы для среднеуглеродистой стали (для циклов с по­ложительными средними напряжениями) показан на рис 8.15. На этой диаграмме каждый цикл изображен двумя точками. Так, предель­ный симметричный цикл изображен точками А и А,; точка В соот­ветствует предельным постоянным напряжениям (); предельный отнулевой (пульсирующий) цикл ()изображен точками С и F.

Чтобы определить предел выносливости для цикла с коэффици­ентом асимметрии, равным R, по диаграмме, построенной по экс­периментальным данным, из начала координат надо провести луч под углом к оси абсцисс. Тангенс этого луча определяется по формуле:

Ордината точки К пересечения этого луча с линией предельных напряжений дает величину .

Для получения области циклов, безопасных в отношении как усталостного разрушения, так и возникновения текучести, на луче ОВ (точки этого луча соответствуют постоянным во времени напряжениям: следует взять точку, изображающую цикл, для которого (точка Т на рис. 8.15), и провести из нее две прямые, кап показано на рисунке. Область безопасных циклов ограничена отрезком AA_i оси ординат, кривыми AS, A,S, и ломаной STS_I.

Рис. 8.15