Вторая серия исследований
Решение
Выдвигаем статистические гипотезы:
Н0 – отличия в тактильной чувствительности до и после корректирующей работы несущественны;
Н1 – отличия существенны.
1) Выясним с помощью критерия знаков, способствовала ли корректирующая работа увеличению порогов тактильной чувствительности.
Составим расчетную таблицу:
| № испытуемого | Уровень тактильной чувствительности «до» корректирующей работы (1 серия испытаний) | Уровень тактильной чувствительности «после» корректирующей работы (2 серия испытаний) | Сдвиг |
| + 4 | |||
| + 2 | |||
| + 11 | |||
| + 4 | |||
| – 4 | |||
| + 1 | |||
| + 5 | |||
| + 4 | |||
| – 5 | |||
| – 1 | |||
| – 12 | |||
| – 5 | |||
| + 3 | |||
| + 2 | |||
| – 10 | |||
| – 8 |
Общее количество нулевых сдвигов – 0;
Типичный сдвиг (в этом случае – положительный) 9;
Нетипичный сдвиг (в этом случае – отрицательный) Gэмп =7.
По таблице 4 приложения определяем критические значения G- критерия при уровнях значимости Р =0,05 и Р =0,01 и количество сдвигов (сумма типичных и нетипичных) n =9+7=16. Получаем:
| n | Р | |
| 0,05 | 0,01 | |
Ось значимости:

G эмп попало в зону незначимости, значит принимается гипотеза Н0, то есть корректирующая работа не привела к существенным изменениям в порогах тактильной чувствительности.
2) Выясним с помощью статистического критерия T -Вилкоксона, повлияла ли корректирующая работа на увеличение порогов тактильной чувствительности.
| № п/п | "До" | "После" | Сдвиг | Абсолютный сдвиг | Ранг абсолютного сдвига |
| + 4 | 7,5 | ||||
| + 2 | 3,5 | ||||
| + 11 | |||||
| + 4 | 7,5 | ||||
| – 4 | 7,5 | ||||
| +1 | 1,5 | ||||
| + 5 | |||||
| + 4 | 7,5 | ||||
| – 5 | |||||
| – 1 | 1,5 | ||||
| – 12 | |||||
| – 5 | |||||
| + 3 | |||||
| + 2 | 3,5 | ||||
| – 10 | |||||
| – 8 |
Столбец "Сдвиг" находят как разницу столбца "после" и столбца "до". В столбец "абсолютный сдвиг" переписываем числа из столбца "сдвиг" без знаков. В столбце "ранг абсолютного сдвига" минимальному из элементов (в данном случае это 1) нужно предоставить ранг 1. Однако, в нашем примере таких чисел два, они занимают 1 и 2 порядковые места, им приписывают усредненный ранг (1+2)/2=1,5 Следующий по величине абсолютный сдвиг 2 встречается также дважды, они занимают 3 и 4 порядковые места, им приписывают ранг (3+4) /2=3,5 и так далее.
Т эмп численно равняется сумме рангов нетипичных сдвигов. В нашем случае нетипичных сдвигов семь (это все отрицательные значения сдвигов). Сумма их рангов равняется:
Т эмп =7,5+11+1,5+16+11+14+13=74.
Далее оценка статистической достоверности сдвига по критерию проводиться по таблице 5 (смотри Приложение). Поиск критических величин по таблице проводится по количеству испытуемых. В нашем случае n =16, потому часть таблицы выглядит так:
| n | Р | |
| 0,05 | 0,01 | |
Ось значимости: 
Т емп попало в зону незначимости, значит принимается гипотеза Н0, то есть корректирующая работа не повлияла на существенное увеличение порогов тактильной чувствительности.
Задание 3
При измерении пространственных порогов тактильной чувствительности получены следующие величины порогов для женщин (данные представлены в таблице в соответствии с Вашим вариантом) и мужчин (данные представлены в таблице следующего варианта).
Необходимо:
1) статистические данные, полученные в результате эксперимента (отдельно для женщин и мужчин) представить в виде статистического ряда, рассчитать их среднее выборочное, ошибки средних, среднее выборочное квадратичное отклонение;
2) с помощью критерия Стьюдента выяснить, являются ли статистически значимыми отличия между средними значениями двух выборок;
3) с помощью критерия числа инверсий (U- Вилкоксона - Манна-Уитни) выяснить, будут ли статистически достоверными отличия между величинами порогов тактильной чувствительности у женщин и мужчин.
Сделайте выводы о наличии (или отсутствие) существенной разницы между уровнями порогов тактильной чувствительности женщин и мужчин.
Пороги тактильной чувствительности у женщин (мм) (Распределение X)
Пороги тактильной чувствительности у мужчин (мм) (Распределение Y)
Решение
1) Распределение X (пороги тактильной чувствительности у женщин)
Статистический ряд
| хi | |||||||||||
| ni |
Объем выборки n =16
Среднее выборочное
 (27×2+28+29+30×2+31×2+32+34+35×2+36×2+38+39)/16=32,38
(27×2+28+29+30×2+31×2+32+34+35×2+36×2+38+39)/16=32,38
Дисперсия
D(X)= (2×272+282+292+302×2+312×2+322+342+352×2+362×2+382+392)/16–32,382=13,9
Среднее выборочное квадратическое отклонение

Ошибка средней определяется по формуле:  m=3,7/4=0,9
m=3,7/4=0,9
1) Распределение Y (пороги тактильной чувствительности у мужчин)
Статистический ряд
| yj | |||||||||||
| nj |
Объем выборки n =16
Среднее выборочное
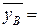 31,81
31,81
Дисперсия
D(Y)= 11,4
Среднее выборочное квадратическое отклонение

Ошибка средней определяется по формуле:  m=3,4/4=0,84
m=3,4/4=0,84
2) С помощью критерия Стьюдента выясним, являются ли статистически значимыми отличия между средними значениями двух выборок.
Вычислим эмпирическое значение критической статистики

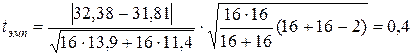
Примем уровень значимости a=0,01.
Определим по таблице критическое значение 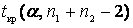 для соответствующего уровня значимости и данного числа степеней свободы
для соответствующего уровня значимости и данного числа степеней свободы 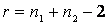 т.е. r= 16+16-2=30. То есть,
т.е. r= 16+16-2=30. То есть,  .
.
tэмп =0,4 < 2,75= tкр (0,01;30), то есть, гипотеза о несущественности отличий средних значений пространственных порогов тактильной чувствительности на уровне значимости α =0,01 принимается.
Можно говорить о приблизительно одинаковом уровне чувствительности у женщин и мужчин.
3) С помощью критерия числа инверсий (U- Вилкоксона-Манна-Уитни) выясни, будут ли статистически достоверными отличия между величинами порогов тактильной чувствительности у женщин и мужчин;
Сформулируем статистические гипотезы:
Н0 – отсутствуют статистически достоверные отличия между величинами порогов тактильной чувствительности у женщин и мужчин;
Н1 –имеются статистически достоверные отличия между величинами порогов тактильной чувствительности у женщин и мужчин.
Представим ряд в виде таблицы, в которую прибавлены еще два столбца для подсчета инверсий (табл.5)
Инверсии X/Y подсчитываются таким образом: число 27 первого столбца не имеет перед собой ни одного числа второго столбца, поэтому в третьем столбце напротив 27 пишем ноль; число 28 первого столбца имеют перед собой 2 числа второго столбца (27, 27), потому в третьем столбце напротив 28 ставим 2. И так далее. Таким образом, суммарное число инверсий X/Y третьего столбца равняется 126. То есть U (X/Y) =126.
Аналогичным способом подсчитывают суммарное число инверсий Y/X четвертого столбца, который равняется 108, U (Y/X) =108.
Таблица 5
| X | Y | Инверсия X/Y | Инверсия Y/X |
| Суммы инверсий |
Считают, что Uэмп минимальная из сумм инверсий. Имеем Uэмп =108.
По таблице 7 Приложения определяем критическое значение U- критерия при уровнях значимости Р =0,05 и Р =0,01 и количеством испытуемых n1 =16 и n2 =16. Получаем:
| n1/ n2 | Р | |
| 0,05 | 0,01 | |
| 16/16 |
Ось значимости: 
U эмп попало в зону незначимости, следовательно принимается гипотеза Н0, то есть отсутствуют статистически достоверные отличия между величинами порогов тактильной чувствительности у женщин и мужчин.
Задание 4
Предоставлены данные, которые характеризуют зависимость признака Y (объем непроизвольного запоминания) от признака Х (объем запоминания после первого предъявления в эксперименте по заучиванию двузначных чисел). На основе этих данных:
- построить корреляционное поле;
- вычислить выборочный коэффициент корреляции;
- найти выборочное уравнение линейной регрессии, которое описывает корреляционную зависимость Y от Х. Нанести полученное уравнение на корреляционное поле.
| Y | Х | |||||
| – | – | – | – | |||
| – | – | – | – | |||
| – | – | – | ||||
| – | – | – | – | |||
| – | – | – | – |
Решение.
Построим корреляционное поле:

Составим расчетную таблицу:
Таблица 6
| Y | Х | nyі | 
| 
| 
| nxyXY | |||||
| – | – | – | – | ||||||||
| – | – | – | – | ||||||||
| – | – | – | |||||||||
| – | – | – | – | ||||||||
| – | – | – | – | ||||||||
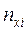
|  604 604
| ||||||||||

|  32 32
| ||||||||||
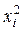
| |||||||||||

| |||||||||||
| nxyXY |




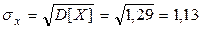
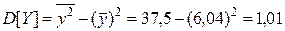
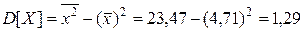
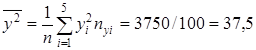
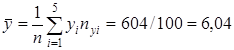
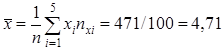
Значит, уравнение линейной регрессии имеет вид:
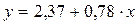
Выборочный коэффициент корреляции:
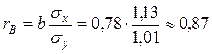 |
То есть, связь между признаком Y (объемом непроизвольного запоминания) и признаком Х (объемом запоминания после первого предъявления в эксперименте по заучиванию двузначных чисел) очень тесна.
Нанесем полученное уравнение на корреляционное поле:
