РЕКОМЕНДАЦИИ ПО РЕШЕНИЮ ТИПОВЫХ ЗАДАЧ

 

1. Измерение в психологии

2. Основные понятия математической статистики. Выборочный метод

3. Числовые характеристики распределения

4. Законы распределения

5. Оценивание и проверка гипотез.

6. Статистические критерии отличий.

7. Непараметрические критерии для связанных выборок.

8. Критерии согласия распределений и многофункциональный критерий "j"

9. Параметрические критерии отличий.

10. Дисперсионный анализ экспериментальных данных

11. Корреляционный анализ.

12. Регрессионный анализ.

13. Основы факторного анализа

 

РЕКОМЕНДАЦИИ ПО РЕШЕНИЮ ТИПОВЫХ ЗАДАЧ

 

Задание 1

 

Результаты, полученные в эксперименте по заучиванию ряда из x_max чисел для 100 испытуемых, предоставлены в таблицах (данные условны). Выбрав данные в соответствии со своим вариантом для признака Х выполнить следующее:

1. Выстроить данные в статистический ряд (по возрастанию);

2. Построить статистическое распределение выборки (вариационный ряд), вычислить относительные частоты;

3. Построить полигон частот. Согласно виду полигона частот выдвинуть гипотезу о законе распределения;

4. Найти эмпирическую функцию распределения и построить ее график;

5. Найти числовые характеристики меры рассеяния: вариационный размах; выборочную среднюю, дисперсию, среднее квадратичное отклонение (ошибку); стандартное отклонение; найти коэффициент вариации;

6. Найти моду, медиану; привести психологическую интерпретацию полученных результатов;

7. Отметить на полигоне частот значения выборочной средней, моды, медианы; указать какой при этом получен вид асимметрии; сделать вывод;

8. Найти выравнивающие частоты в предположении нормальности распределения; построить нормальную (теоретическую) кривую на том же рисунке, где был построен полигон частот;

9. С помощью критерия Пирсона (c²-критерия) проверить гипотезу о нормальности распределения.

 

 

 

Решение

1. Превратим данные в статистический ряд (по возрастанию)

 

2. Построим статистическое распределение выборки.

 

Статистическим распределением выборки называют перечень вариант х_і и соответствующих им частот n_i (сумма всех частот равняется объему выборки n) или относительных частот w_i (сумма всех относительных частот равняется единице).

 

Построим статистическое распределение выборки. Для удобства дальнейших расчетов в таблицу добавим строки как с частотами, так и с относительными частотами.

 

xi
ni
wi	0,03	0,24	0,45	0,18	0,08	0,02

 

Объем выборки составляет:

n =3+24+45+18+8+2=100.

 

Относительные частоты рассчитываются по формуле

 

При этом выполняется: 0,03+0,24+0,45+0,18+0,08+0,02=1.

 

3. Построим полигон частот.

 

Полигоном частот называется ломаная, отрезки которой соединяют точки с координатами (x ₁, n ₁),...,(x _m, n _m).

 

 

xi

ni

По виду полигона частот выдвинем гипотезу о нормальном законе распределения.

 

4. Найдем эмпирическую функцию распределения и построим ее график.

 

Эмпирической функцией распределения называют функцию 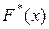, которая определяет для каждого значения х относительную частоту события Х<х, то есть где 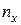– число вариант, меньших х, n – объем выборки.

Наименьшая варианта равняется 4, значит

F^*(x) =0 при .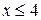

Значение Х<7, а именно х₁ =4, наблюдалось 3 раза, значит

F^*(x) =3/100=0,03 при .

Значение Х<10, а именно х₁ =4 та х₂ =7, наблюдалось 3+24=27 раз, значит

F^*(x) =27/100=0,27 при .

Продолжив аналогично, получим функцию распределения:

 

Замечание. Обратите внимание на то, что при правильных расчетах значение функции распределения при х больше самой большой варианты (в нашем случае x>19) равняется единице.

 

График функции распределения:

 

F*(x)

xi

5. Найти числовые характеристики меры рассеивания, вариационный размах; выборочную среднюю, дисперсию, среднее квадратическое отклонение (ошибки); найти коэффициент вариации.

 

Размах вариации R = x _max- x _min

 

R = 19 – 4 = 15

 

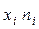Найдем выборочную среднюю, дисперсию, среднее квадратическое отклонения, для этого составим расчетную таблицу:

xi	ni

Среднее квадратическое по формуле (5):

Стандартное отклонение по формуле (6):

 

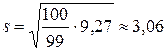
Коэффициент вариации

 

 

6. Найдем моду, медиану; приведем психологическую интерпретацию полученных результатов.

Мода отвечает варианте с наибольшей частотой:

Мо =10

Таким образом, среднее количество заученных чисел равняется приблизительно 10.

 

Медианой (Mе) называется такое значение вариационного признака, которое выпадает на середину вариационного ряда. При вычислении медианы дискретного вариационного ряда могут возникнуть два случая:

1) число вариант непарное (n=2m+1),

2) число вариант парное (n =2m).

В первом случае M e= x _m+1, медиана равняется центральной (серединной) варианте ряда, это варианта с номером m=(n-1)/2;

В другом случае M e=(x _m+ x _m+1)/2, медиана равняется полусумме, которая находится в середине ряда вариант, где n=k/2.

 

Основываясь на том, что n =100

m =100/2=50

Таблица 2

i	xi	ni	Накопленные частоты

 

Первый интервал, который превышает 50 – третий, то есть х₅₀= х₅₁=10.

Me =(10+10)/2=10.

Значение медианы имеет следующую интерпретацию: чуть больше двух третьих испытуемых запомнила меньше или ровно 10 слов, а вторая часть – больше 10 слов.

 

7. Обозначить на полигоне частот значения выборочной средней, моды, медианы; указать, какой вид асимметрии при этом получено; сделать вывод;

Мо, Ме

Если график распределения имеет правостороннюю асимметрию ("хвост" вправо), то в этом случае мода размещена левее, а среднее арифметическое – правее медианы (см. рисунок).

Действительно, левее и правее медианы размещены одинаковые площади, но левой части отвечает меньшая основа, а правой - большая основа. Поэтому левая часть кривой выше правой, и мода будет находиться левее медианы. По этой самой причине медиана не может служить точкой равновесия, поскольку площадь части, соответствующей большей основе, больше площади, размещенной на меньшей основе. Следовательно, среднее арифметическое находится правее медианы.

Таким образом, при правосторонней асимметрии левее расположена мода, дальше медиана и правее – среднее арифметическое. Обратное расположение имеет место при левосторонней асимметрии графика. При этом, чем более асимметричный график, тем больше расстояние между его средними точками.

 

В нашем случае мода размещена левее, а среднее арифметическое – правее медианы, то есть график распределения имеет правостороннюю асимметрию. Зато, разница между средним арифметическим, модой и медианой незначительна, то есть распределение приближено к нормальному.

8. Найдем выравнивающие частоты, допуская, что распределение является нормальным.

Выравнивающие (теоретические) частоты рассчитывают по формуле:

(8)

Рассчитаем теоретические частоты (смотри следующую таблицу). Для этого определим нормируемые отклонения (графа 3) по формулам

(9)

По приложению устанавливаем значение функции (графа 4), рассчитываем теоретические частоты по формуле (8) (графа 5):

 

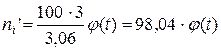
Таблица 3

i	xi	ti
		-2,06	0,0478	4,7
		-1,08	0,2227	21,8
		-0,10	0,397	38,9
		0,88	0,2709	26,6
		1,86	0,0707	6,9
		2,84	0,0071	0,7
Σ				99,6

9. Построим на полигоне частот нормальную (теоретическую) кривую:

ni, ni'

10. Проверим при уровне значимости гипотезу о нормальном распределении генеральной совокупности по критерию Пирсона.

 

а) Составим расчетную таблицу (4) по которой найдем наблюдаемое

(10)

Таблица 4

i
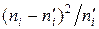
		4,7	-1,7	2,8	0,6
		21,8	2,2	4,7	0,2
		38,9	6,1	36,9	0,9
		26,6	-8,6	73,3	2,8
		6,9	1,1	1,1	0,2
6		0,7	1,3	1,7	2,4
Σ		99,6	0,4		7,1

 

Из таблицы 4 получаем 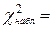7,1.

б) По таблице критических точек (смотри приложение 3), по уровню значимости и числу степеней свободы (тут m=6 – количество вариант) находим критическую точку правосторонней критичной области (табл. 3 Приложения).

Учитывая, что – гипотезу о нормальном распределении генеральной совокупности принимаем. То есть, эмпирические и теоретические частоты отличаются незначительно.

 

Задание 2

 

Проведены две серии испытаний по измерению пространственных порогов тактильной чувствительности (в мм). Данные, полученные в первой серии испытаний, представлены в таблицах в соответствии с Вашим вариантом. Данные, полученные во второй серии, представлены в таблице следующего варианта.

Способствовала ли корректирующая работа увеличению порогов тактильной чувствительности?

Решить задание двумя способами:

1) с помощью критерия знаков;

2) с помощью статистического критерия T-Вилкоксона.