Композиция в перспективном рисунке.

Смысл латинского слова «compositio» - сложение, сопоставление, приведение частей в единство. В ши­роком смысле слова, этот термин употребляется в музыке, литературе, театре, кино, архитектуре и в изобра­зительном искусстве. В творческом отношении - это общий замысел, структура произведения искусства, выра­жающая его идею. В техническом отношении - расположение частей и их гармоничная связь между собой.

Рисунок как самостоятельная область искусства подчиняется общим композиционным закономерностям и в то же время имеет свои только ему присущие правила. К таким правилам относится учение о пропорциях в природе и архитектуре, понятия: симметрия, ритм, статика и динамика, а также законы перспективы. Образ­ное мышление подсказывает творческое применение этих правил на практике в той или иной композиции. Композиционные правила.

1. Правила симметрии, вытекающие из пластики строения человеческого тела и множества других природ­ных форм, устанавливающие закон гармонии пропорций, частей и целого организма.

2. Правила равновесия — сочетания противоположных сторон изображения, равновеликих по массам.

3. Правила статики и динамики (покоя и движения) в пластическом решении композиции.

4. Правила ритма — закономерного чередования больших и малых форм, движения и покоя, контрастного и приглушенного, света и тени.

5. Правила перспективы применительно к различным композиционным решениям...

7. Масштаб как мера уменьшения или увеличения по отношению к натуральной величине...

9. Вертикали и горизонтали как постоянные оси по отношению ко всем другим направлениям.

Из книги А.Дейнеки «Учитесь рисовать»

Каждое из этих правил может быть рассмотрено очень подробно. В эпоху Ренессанса почти каждому из правил воспроизведения натуры на плоскости посвящались отдельные трактаты. Такая степень подробности для того, кто только учится рисовать не обязательна. Далее приведены некоторые выдержки из книги А. Дейнеки, более подробно раскрывающие те законы, которые наиболее актуальны для начинающего рисовальщика.

Закон симметрии мы постоянно наблюдаем в природе. Симметрично построена фигура человека. По закону симметрии созданы многие архитектурные сооружения, декор. Одинаковость сторон изображения да­ет понятие равновесия, что можно наблюдать не только в архитектуре, но и во многих произведениях живо­писи, скульптуры, декоративно-прикладного искусства. В композиции, построенной по принципу симметрии, центр может иметь известный акцент - более крупное изображение.

Чувство равновесия в композиции определяется вертикальной осью, которая делит изображение по­полам. Из этого приема вытекает еще одно понятие - статика, чувство зрительной уравновешенности, нес­мотря на сложно-выразительную жестикуляцию отдельных персонажей. Точка схода в подобных случаях всегда будет посередине изобразительной плоскости.

12 глава II

Нарушение равновесия (например, когда точка схода переносится в край или когда сдна сторона более насыщена по массам, чем другая, или кгода, наконец, композиция срроится по диагонали) - рожда-ет начало динамики в изображении.

Правила ритма можно проследить и в композициях произведений изобразительного искусства и в ми- ре природы. Ритм мы видим в самых различных природных формообразованиях - в расположении лепестков цветка, в движении волн и т.д. Простое повторение одинаковых движеий человека дает ощущение ритма. Ритмичные движения легко уловить в трудовых процессах, в танце. Рит лежит в основе хомпозиции худо­жественных произведений, начиная от простейшего орнамента на бытовых вещах и кончая грандиозными фризами. В рисунке ритм может быть передан линией, светотеневыми повторениями.

Перспективные правила в изобразительном искусстве, в частности, в рисунке, имеют первостепенное значение. Построенная на законах математики и оптики, перспектва как наука в руках опытного художника да-ет возможность правильно строить пространство на плоскости и соразмерять между собой предметы...

Эти и другие композиционные правила будут раскрываться перед вами постепенно в процессе обуче­ния, наполняясь новым содержанием по мере усложнения задач вашего рисунка.

Композиция на листе.

Правильно закомпоновать лист (создать хорошую композицию листа) или, иными словами, грамотно и красиво разместить на листе изображение важно в любом рисунке. Плохая композиция заметно снижает все достоинства даже технически безупречно выполненной работы.

Изображая на листе один предмет (например, какое-нибудь геометрическое тело или гипсовую голо­ву), необходимо сначала выбрать правильный размер изображения (чтобы ему не было слишком тесно или слишком просторно), а затем поместить изображение посередине листа, чуть приподнимая его и оставляя, таким образом, снизу больше пространства, чем сверху (рис.8).

 

 

Рис.8

Рис.9

перспективный рисунок простых геометрических тел 13

 

Рис.10 Рис.11

Увеличение количества изображаемых предметов, а также небольшие перспективные зарисовки и ор­тогональные проекции на полях рисунка, безусловно, усложняют композицию листа и ставят перед рисоваль­щиком дополнительную задачу соподчинения главного и второстепенного. Изображения, более важные по смыслу, должны занимать центральное место в рисунке (рис.9).

Лист должен быть заполнен равномерно: предметы не должны собираться в его центре (рис.10), а так­же подходить слишком близко к краю листа (рис. 11).

Перед началом работы нужно тщательно продумать композицию листа. Если размещение будущего изображения на большом листе вызывает у вас серьезные затруднения, необходимо сделать эскиз. Эскиз должен быть достаточно крупным по размеру, иначе вы не сможете перенести его на большой лист без зна­чительных искажений. На эскизе можно решить основные композиционные вопросы: найти общие пропор­ции будущего изображения, размеры отдельных его частей и их место на листе, определить положение ли­нии горизонта, а также направления горизонтальных линий, уходящих в точки схода.

Изобразите все элементы будущего рисунка в мелком масштабе (рис.12), а затем заключите их в рамку, пропорции которой соответствуют пропорциям большого листа (рис.13). В поисках хорошей ком­позиции вы можете перемещать рамку относительно изображения, уменьшать и увеличивать ее, помня о том, что пропорции рамки должны сохраняться. В некоторых случаях приходится менять не только по­ложение и размер рамки, но и само изображение: место и размеры его элементов, линию горизонта, точ­ку зрения. При увеличении эскиза, воспользуйтесь центральной точкой листа - пересечением его диаго­налей (рис.14), которая будет служить дополнительной «точкой отсчета» при определении места и разме­ров отдельных элементов изображения на большом листе (рис.15). Помните, что найденную в небольшом эскизе гармонию не всегда удается полностью сохранить при переносе замысла на полный лист. Старай­тесь поэтому сохранить главную идею и общие закономерности композиции, отработанные в эскизе, творчески изменяя второстепенные и незначительные детали.

14 глава II

 

 

Рис.12

Рис.13

Рис.14

Риc.15

перспективный рисунок простых геометрических тел 15

Рисунок куба в перспективе.

Перспектива куба строится на перспективе квадратов его образующих. Чувство перспективы квадра­та, а также куба должно быть развито у архитектора особенно хорошо, так как квадрат и куб являются ос­новными модулями площади и объема для других плоских и пространственных форм.

Основные правила построения квадрата в перспективе.

1. Чем дальше от линии горизонта (выше или ниже) находится квадрат, лежащий в горизонтальной плоскости, тем большее раскрытие он имеет, и наоборот, чем ближе к линии горизонта, тем меньше он раск­рывается, превращаясь на линии горизонта в отрезок (рис.16).

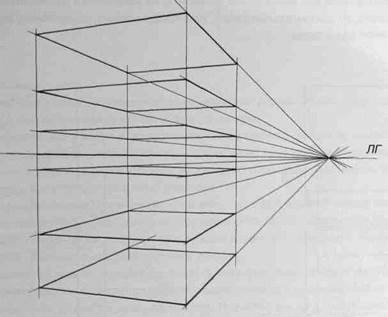
Рис.16

2. Чем дальше находится вертикально расположенный квадрат от точки схода его горизонтальных сто­рон, тем больше он раскрыт, и наоборот, чем ближе к точке схода, тем его раскрытие меньше (рис.17).

Рис.17

16 глава II

3 Чем дальше точка зрения рисующего от квадрата, тем дальше находятся друг от друга точки схода его сторон и тем меньше их перспективные сокращения. И наоборот, чем ближе рисующий к квадрату, тем точки схода ближе друг к другу и перспективные сокращения его сторон больше.

4. В произвольном (негоризонтальном и невертикальном) положении квадрата точки схода его сторон могут быть выше и ниже линии горизонта.

Рассмотрите рисунок 18, на котором изображены кубы во фронтальной перспективе. У куба, распо­ложенного фронтально на уровне горизонта, мы видим только одну переднюю грань. Ребра куба, принад­лежащие фронтальным граням, остаются, параллельными между собой, но изменяются по величине: реб­ра передней фронтальной грани больше ребер задней грани. Горизонтальные ребра, уходящие от нас в глубину, сокращаются по своему размеру и лежат на прямых, пересекающихся в точке схода на горизон­те. Если куб поставить ниже или выше линии горизонта, не изменяя его фронтального положения, види­мыми станут две грани, а горизонтальные ребра, уходящие в глубину, по-прежнему будут сходиться на ли­нии горизонта в одной точке схода.

 

 

Рис.18

Рис.19

Рассмотрите рисунок 19, на котором изображены кубы в угловой перспективе. У куба в угловом положении на уровне горизонта видны две боковые грани. Горизонтальные ребра этого куба имеют две точки схода, расположенные слева и справа от него. Если поставить куб ниже или выше горизонта, не изменяя его поворота, то, кроме боковых граней, будет также видна верхняя или нижняя грань, а точки, в которых сходятся горизонтальные ребра, не изменят своего положения. Как правило, точки схода находятся достаточно далеко друг от друга и не попадают в плоскость листа (рис.20). Рассмотрев различные положения куба, зарисуйте его в угловом положении с натуры. Старайтесь сначала вести рисунок на глаз, а затем, если есть сомнения,

проверяйте его, пользуясь приемом визирования. Этот прием позволяет с достаточной точностью переносить
на лист габариты изображаемых предметов, определять размеры их частей по отношению к общему, а также
фиксировать направления наклонных прямых.

перспективный рисунок простых геометрических тел 17

Рис.20

Прием визирования.

При определении пропорций натуры приемом визирования рисующий использует размер какого-либо предмета как единицу измерения любых других размеров натуры:

1. Руку с карандашом вытягивают в направлении изображаемого предмета, например, куба, при этом карандаш занимает перпендикулярное положение к направлению луча зрения. Расстояние между глазом и карандашом не должно изменяться, для этого руку необходимо полностью распрямить. В противном случае невозможно будет добиться точности сравнения размеров.

2. Зрительно совместив конец карандаша, например, с крайней верхней точкой изображаемого пред­мета, вертикальный размер которого выбран за основу измерения, нужно передвинуть большой палец на ка­рандаше до зрительного совмещения края пальца с нижним краем этого предмета. Карандаш в данном слу­чае выполняет функцию измерительного инструмента (рис.21).

3. Не меняя положения пальцев и держа карандаш в вытянутой руке, придают ему горизонтальное поло­жение. В этом положении зрительно совмещают край большого пальца с правым краем предмета и зрительно отмечают, против какой точки находится конец карандаша. Иначе говоря: на длине предмета мы откладываем размер его высоты (рис.22). Затем передвигают этот условный размер еще влево, причем так, чтобы край боль­шого пальца зрительно совпадал на предмете с той точкой, которая только что отмечалась концом карандаша (рис.23). Таким образом, мы определяем, во сколько раз один из габаритов предмета больше другого.

Рис.21 Рис.22 Рис.23

Начните рисунок куба, с нанесения на бумагу общих габаритов легкими горизонтальными и верти­кальными штрихами (рис.24). Затем определим положение переднего вертикального ребра (первый план), на котором отложите высоту куба и наметьте наклоны горизонтальных ребер, начиная с нижней точки (рис.25).

18 глава II

 

 

Рис.24

Рис.25

 

 

 

Рис.26

Рис.27

перспективный рисунок простых геометрических тел 19

Для верной передачи перспективы горизонтальных линий (в нашем примере - ребер куба) также пользуются приемом визирования. Руку с карандашом вытягивают в сторону натуры. Карандаш держат горизонтально, располагая его перпендикулярно направлению взгляда. Подводя карандаш к линиям на­туры, определяют их наклон по отношению к горизонтальному положению карандаша. Для контроля пра­вильности полученного наклона линий нужно и на рисунке провести вспомогательную горизонталь. От­метим, что у более широко раскрытой грани горизонтально расположенного куба угол наклона удаляю­щихся в глубину ребер (α) меньше, чем у грани, сильнее сокращенной в перспективе, а значит - менее раскрытой (β).

Продолжая рисовать куб, намечаем наклоны всех уходящих в глубину ребер и определяем высоту вертикальных ребер на втором плане (рис.26). Изображая верхнюю грань куба, важно показать, что она в перспективе сокращается больше, чем нижняя, так как находится ближе к горизонту. Для уяснения конструкции предмета и контроля правильности рисунка необходимо прорисовать невидимые ребра ку­ба. Линии уходящих в глубину ребер нужно в пределах листа продолжить и проследить степень их сбли­жения в перспективе (рис.27). Закончив рисунок, полезно сделать ряд набросков куба в других, рассмот­ренных ранее положениях с целью закрепления навыков, развития глазомера и пространственного представления.

Рисунок четырехгранной призмы.

Наилучшее представление о геометрическом теле дает анализ его ортогональных проекций (рис.28). Основаниями четырехгранной призмы являются квадраты, боковыми гранями - одинаковые по размеру пря­моугольники, соотношение сторон которых определяет пропорции призмы. Так, если принять длину стороны квадрата основания за а, то меньшая сторона прямоугольника боковой грани также будет равна а, его боль­шая сторона (в нашем примере) - 1,5а, а пропорции призмы -1 к 1,5.

Рис.28

Основой для построения прямоугольника в перспективе является перспективное построение квадра­та: так, сначала необходимо построить квадрат со стороной, равной меньшей стороне прямоугольника (а), а затем удлинить одну из сторон квадрата до заданного отношения (7,5а). При рисовании четырехгранной призмы заданных пропорций сначала изображают куб, а затем удлиняют его по вертикали (рис.29) или го­ризонтали (рис.30), в зависимости от положения призмы. Определяя размеры горизонтально расположен­ной призмы, помните о сокращении отрезков, лежащих на горизонтальной прямой.

Важным моментом в изучении конструкций геометрических тел является построение их сечений вертикальными и горизонтальными плоскостями (иначе говоря, плоскостями параллельными и перпенди­кулярными плоскости основания). Сечениями куба и четырехгранной призмы являются квадраты и пря­моугольники, построение которых не представляется сложным, а потому и не рассматривается нами.

20 глава II

 

 

Рис.29

Рисунок четырехгранной пирамиды.

Рис.30

Основанием четырехгранной пирамиды является квадрат со стороной а, ее боковыми гранями - одина­ковые по размеру треугольники. Высота пирамиды по отношению к стороне квадрата основания определяет ее пропорции (высокая или приземистая). В нашем случае высоту пирамиды примем равной 1Да (рис.31).

Рис.31

Начинать построение стоящей пирамиды необходимо с изображения квадрата основания. Через точ­ку пересечения его диагоналей проводим вертикаль, на которой откладываем отрезок, равный высоте пи­рамиды - 1,5a (рис.32). Соединяя полученную таким образом вершину пирамиды с вершинами квадрата ос­нования, получим перспективный рисунок четырехгранной пирамиды (рис 33)

При вертикальном положении пирамиды ее горизонтальные сечения - квадраты, разных размеров в зависимости от положения секущей плоскости (рис.34). Вертикальное сечение, проходящее через вер­шину пирамиды и параллельное стороне квадрата основания, представляет собой треугольник, основа-

перспективный рисунок простых геометрических тел 21

ние которого равно а, высота равна высоте пирамиды, а боковая сторона является высотой в треуголь­нике боковой грани. Все другие, параллельные этому, вертикальные сечения пирамиды, являются трапе­циями, большее основание которых равно а, меньшее - меняется в зависимости от положения плоскости сечения, а боковые стороны параллельны высотам в треугольниках боковых граней (рис.35).

Рисунок пирамиды, лежащей на горизонтальной плоскости, сложнее рисунка стоящей пирамиды из-за трудности в определении положения квадрата ее основания. Опытный рисовальщик легко решает подобные задачи, начинающему рисовальщику для приобретения навыков изображения геометрических тел по предс­тавлению, необходимо выполнить достаточное количество рисунков с натуры, используя прием визирования и обращая особое внимание на конструктивные особенности, а также изменение видимых пропорций тел в зависимости от изменения точки зрения рисующего.

Рис.32 Рис.33

 

Рис.34 Рис.35

глава II

Рисунок цилиндра.

Цилиндр - геометрическое тело, относящееся к так называемым телам вращения, то есть цилиндр можно получить путем вращения прямоугольника вокруг одной из его сторон. Основаниями цилиндра явля­ются окружности. Ось цилиндра соединяет центры окружностей оснований и перпендикулярна им. Пропор­ции цилиндра определяются отношением диаметра основания к его высоте, в нашем примере -1:1.5 (рис.36).

Рис.36

Окружность в перспективе изображается как эллипс (рис. 37). Получить эллипс можно путем сечения цилиндра или конуса, когда плоскость сечения пересекает все образующие. Две оси эллипса - большая и ма­лая - перпендикулярные прямые, пересекающиеся в центре эллипса. Отношение малой оси эллипса к боль­шой называется раскрытием эллипса. На большой оси на равных расстояниях от центра эллипса лежат точ-ки f1 и 12 - фокусы эллипса. Любая точка, принадлежащая эллипсу, подчинена формуле: а + b = const, где а и Ь - расстояния от данной точки до фокусов эллипса. Эллипс является нециркульной кривой в отличие от овала, применяемого для изображения окружности в аксонометрических проекциях.

Для того чтобы лучше понять особенности изображения эллипса начертите его следующим обра­зом. Возьмите лист бумаги и закрепите его на подрамнике, в центре листа наметьте точку центра эллип­са и проведите через нее малую и большую оси под прямым углом друг к другу. На равных расстояниях от центра эллипса на большой оси обозначьте фокусы эллипса. Воткните в точки f 1 и f 2 кнопки и привя­жите к ним тонкую бечевку, зафиксировав ее длину. Затем, при помощи карандаша, не отрывая его от листа и не ослабляя натяжения бечевки, начертите эллипс (рис. 38).

 

 

Рис.37

Рис.38

перспективный рисунок простых геометрических тел

Изменяя расстояние между фокусами путем перекалывания кнопок, можно начертить эллипсы раз­ного раскрытия. Увеличивая расстояние между фокусами, вы получите эллипсы с меньшим раскрытием, при уменьшении расстояния между фокусами раскрытие эллипса увеличивается. Когда фокусы эллипса предельно отдалены друг от друга и расстояние между ними равно длине бечевки (а + Ь), эллипс превра­щается в отрезок. Когда фокусы сходятся в одной точке - центре эллипса, он превращается в окружность. Отрезок и окружность являются крайними случаями изображения эллипса, соответствующими его мини­мальному и максимальному раскрытию.

Рисунок эллипса следует начать с изображения его осей. Для окружности, лежащей в горизонтальной плоскости, большая ось эллипса будет горизонтальной прямой, малая - вертикальной. Отложите от центра эллипса равные расстояния по большой и равные расстояния по малой оси, определив, таким образом, его раскрытие. Через полученные на осях четыре точки проведите эллипс, стараясь придать его очертанию пра­вильный характер. Сравните нарисованный эллипс с эллипсом, начерченным при помощи кнопок и бечевки, проследите симметрию эллипса относительно большой и малой осей. Исправьте замеченные ошибки. Уп­ражняйтесь в изображении эллипсов разного размера и раскрытия, добиваясь быстроты и четкости рисунка. Помните, что грамотное построение эллипса является обязательным для профессионального рисовальщика.

Центр эллипса и центр окружности - две разные точки. Это хорошо видно на примере окружности, вписанной в квадрат, во фронтальной перспективе (рис.39). Диаметр окружности, являющийся малой осью эллипса делится точкой центра окружности на два разных по величине отрезка: ближний к зрителю - боль­ше, дальний - меньше (по закону перспективного сокращения), а точка центра эллипса делит этот же диа­метр - малую ось эллипса - ровно пополам.

Освоив рисунок эллипса, вы легко перейдете к рисованию цилиндра.

Рис.39