Вертикальный шестиугольник.

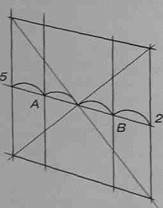
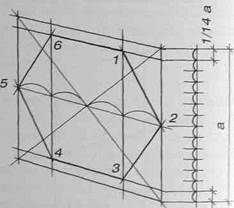
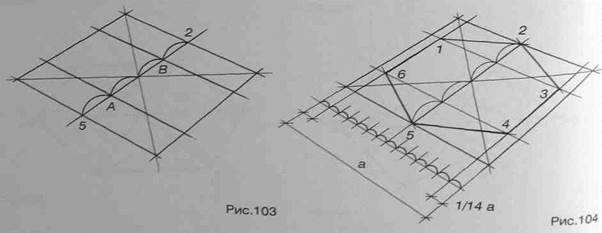
Нарисуйте вертикальный квадрат в перспективе. Проведите через пересечение диагоналей прямую, параллельную его горизонтальным сторонам. Разделите полученный отрезок 5-2 на четыре равные части и проведите через точки А и В вертикальные прямые (рис.101). Линии, ограничивающие шестиугольник свер­ху и снизу, не совпадают со сторонами квадрата. Изобразите их на некотором расстоянии (1/14а) от горизон­тальных сторон квадрата и параллельно им. Соединив найденные таким образом точки 1 и 3 с точкой 2, а точки 6 и 4 с точкой 5, получим шестиугольник (рис.102).

Горизонтальный шестиугольник строится в той же последовательности (рис.103 и 104).

Использование этого способа, как и способа на основе прямоугольника, уместно только для шестиу­гольника с достаточным раскрытием. В случае, когда раскрытие шестиугольника незначительно, лучше вос­пользоваться способом построения на основе описанной окружности.

 

 

Рис.101

Рис.102

перспективный рисунок простых геометрических тел 41

Овладев навыками изображения шестиугольника, вы свободно перейдете к изображению шестигран­ной призмы. В нашем примере высота шестигранника равна 7,5а, где а - диаметр описанной вокруг основа­ния окружности (рис.105).

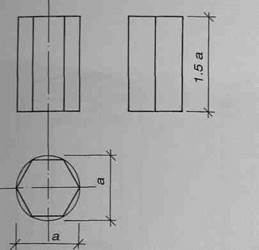
Рис.105

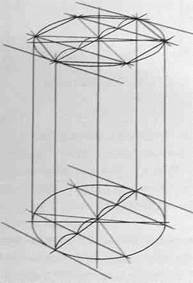
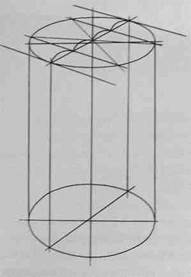
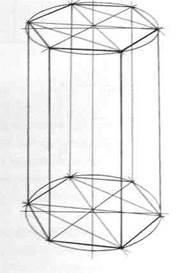
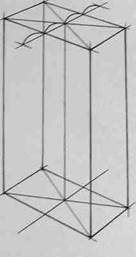
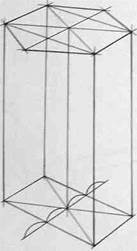
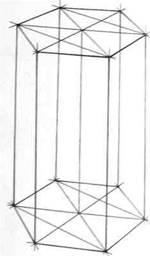
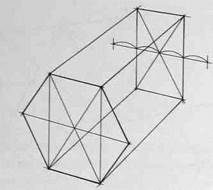
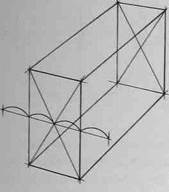
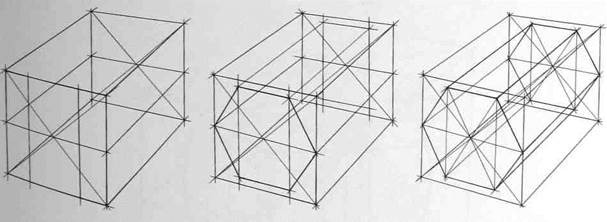
Внимательно рассмотрите схему на рис.106, а также схемы построения шестигранных призм на осно­ве описанной окружности (рис.107,108 и 109), на основе прямоугольника (вертикального - рис.110,111 и 112, горизонтального - рис.113, 114 и 115), а также на основе квадрата (рис.116, 117 и 118). Изобразите верти­кальные и горизонтальные шестигранники всеми предложенными способами.

Рис.106

42 глава II

 

 

Рис.107

Рис.108

Рис.109

 

 

 

Рис.110

Рис.111

Рис.112

перспективный рисунок простых геометрических тел 43

 

 

Рис.113

Рис.114

Рис.115

 

 

 

Рис.116

Рис.117

Рис.118

44 глава II

 

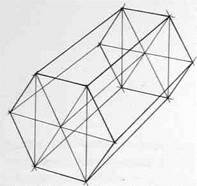
На рисунке вертикального шестигранника длинные стороны боковых граней будут параллельными друг другу вертикальными прямыми, а шестиугольник основания будет тем больше раскрыт, чем дальше он находится от линии горизонта. На рисунке горизонтального шестигранника длинные стороны боковых гра­ней будут сходиться в точке схода на горизонте, а раскрытие шестиугольника основания будет тем боль­ше, чем дальше от зрителя он находится. Изображая шестигранник, следите также за тем, чтобы парал­лельные грани обоих оснований сходились в одной точке (рис.119,120).

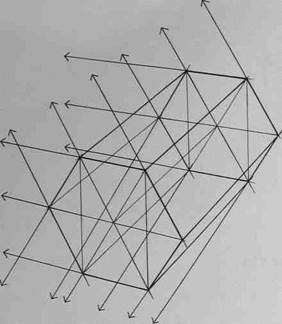
Рис.119

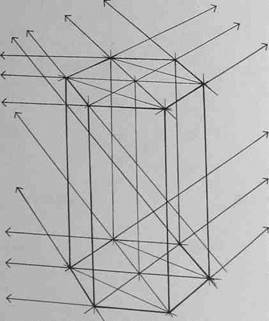
Рис.120

перспективный рисунок простых геометрических тел 45

Рисунок шара.

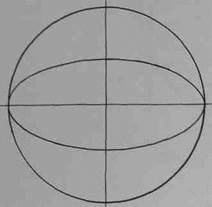
Шар с любой точки зрения воспринимается человеческим глазом одинаково, поэтому в перспективном рисунке он всегда изображается как окружность. Нарисуйте в перспективе шар, лежащий на горизонтальной плоскости: проведите две оси (вертикальную и горизонтальную), отложите на них одинаковые отрезки, рав­ные радиусу шара, и соедините четыре полученные точки дугами (рис.121). Уточняя рисунок, можно провес­ти дополнительные оси и также отложить на них отрезки, равные радиусу.

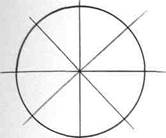
Рис.121

Полученное изображение, однако, еще не шар, оно не имеет объема. Для того чтобы в линейном ри­сунке придать окружности шарообразный объем, необходимо изобразить три взаимно перпендикулярные се­чения, проходящие через центр шара. Мы построим эти сечения при помощи куба, грани которого, как изве­стно, также лежат во взаимно перпендикулярных плоскостях.

Рассмотрите рисунок шара, вписанного в куб, стоящий на горизонтальной плоскости (рис.122). Диа­метр шара равен длине ребра куба, и шар касается каждой из шести граней куба в ее центре (т. е. в точке пересечения диагоналей). Обозначим точки касания 1-6.

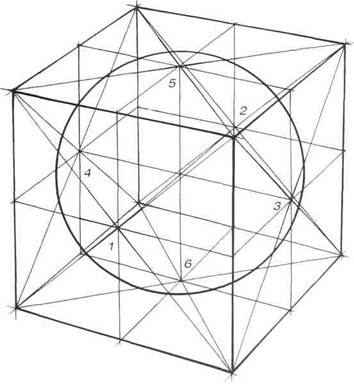
Рис.122

глава II

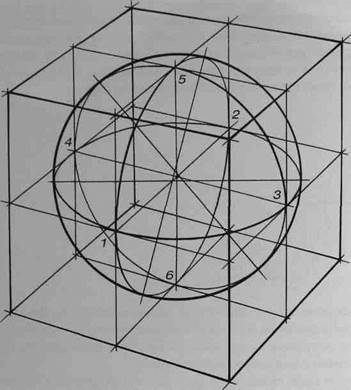
Рис 123

На рисунке 123 куб с шаром рассечены тремя взаимно перпендикулярными плоскостями, параллельными граням куба и проходящими через центр шара. Секущие плоскости в таком случае пересекаются друг с другом по трем взаимно перпендикулярным прямым, параллельным ребрам куба и соединя­ющим середины противоположных граней, т.е. точки 1-2,3-4 и 5-6. Каждое из трех сечений представляет собой квадрат с вписанной в него окружностью, причем окружности касаются сторон квадратов в точках 7-6, как, например, на рисунке 124.

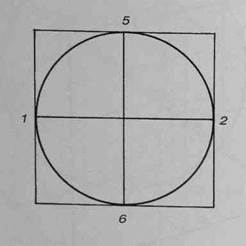
Рис.124

перспективный рисунок простых геометрических тел 47

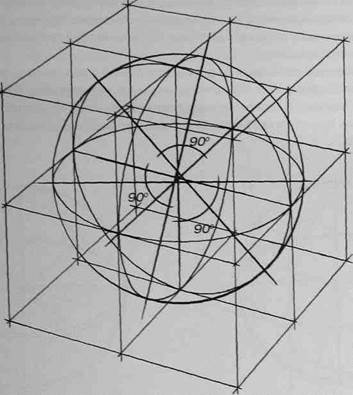
Рис.125

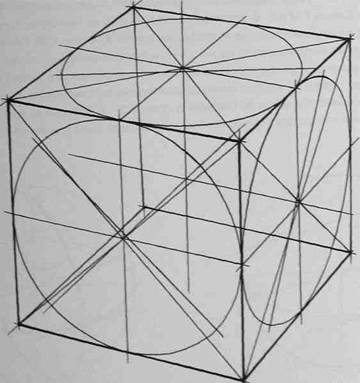
Рис.126

глава II

Малые оси эллипсов сечения шара, параллельны ребрам куба, а большие оси, как обычно, им перпен­дикулярны (рис.125). Эти наблюдения позволят нам решить задачу построения трех взаимно перпендикулярных сечений шара. Обратите внимание на то, что эллипсы сечения шара по своему раскрытию будут соотве­тствовать эллипсам, вписанным в грани куба (рис.126). Это поможет вам точнее представить эллипсы сече­ния шара перед началом построения.

Возьмите за основу уже сделанный рисунок шара в виде окружности с горизонтальной и верти­кальной осями. Изобразите на этих осях горизонтальный эллипс - сечение шара горизонтальной плоскостью (рис.127). Его раскрытие зависит от положения шара относительно линии горизонта. Чем ближе шар к линии горизонта, тем раскрытие меньше, и наоборот, чем дальше шар от линии горизонта, тем больше раскрытие горизонтального эллипса.

 

 

Рис.127

Рис.128

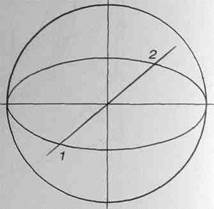
Теперь необходимо найти линии пересечения горизонтального эллипса с вертикальными эллипсами сече­ния - перпендикулярные прямые 1 -2 и З-4. Задайте произвольно одну из этих прямых, например, 1-2 (рис.128), и постройте при помощи касательных перпендикулярную ей прямую 3-4 (рис.129). Обратите ваше внимание на то, что в построении сечения шара мы можем не учитывать смещения центра эллипса относительно центра ок­ружности (шара). Эти смещения в данном случае не изменят сути построения, а только усложнят его.

На нашем рисунке прямая 3-4 будет являться малой осью вертикального эллипса сечения, большая его ось - прямая, проведенная под углом 90 градусов к прямой 3 - 4. Раскрытие этого эллипса определяют точки 1 и 2, через которые он проходит. Изобразите эллипс по двум осям и двум точкам (рис.130).

 

 

Рис.129

Рис.130

перспективный рисунок простых геометрических тел 49

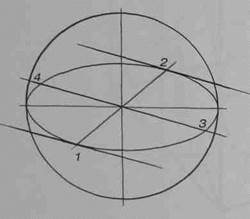
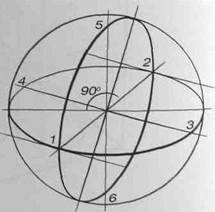
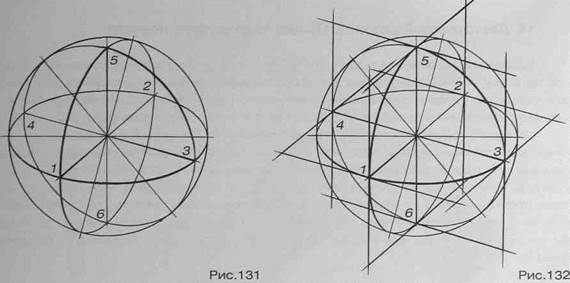
Второй вертикальный эллипс строится аналогично первому. Его малая ось - прямая 1-2, большая ось - перпендикулярная ей прямая, а точки 3 и 4 определяют его раскрытие (рис.131). Вертикальные эллипсы сечения должны пересекаться друг с другом в точках 5 и 6, лежащих на вертикальной прямой, проходящей через центр шара. Правильность построения также можно проверить, проведя касательные к эллипсам се­чения в точках 1-6, они должны быть параллельны соответственно прямым 1 -2,3-4 и 5-6 (рис.132).

Три взаимно перпендикулярные сечения шара не только создадут его объем на перспективном рисун­ке но и помогут вам представить и нарисовать другие сечения шара (не проходящие через его центр), а также найти положение любой точки, лежащей на его поверхности. Постройте сечения нескольких шаров, меняя положение секущих плоскостей относительно зрителя.

глава III

Глава III. Светотеневой рисунок

простых геометрических тел

14. Светотеневой рисунок. Общие положения и понятия.

Изображая геометрические тела, вы, конечно же, заметили, что различная освещенность поверхностей этих тел помотает лучше понять форму и конструкцию предметов. Вводя в линейный рисунок светотень, то есть передавая с помощью тона различную освещенность поверхностей изображаемых предметов, вы смо­жете еще полнее выявить их срорму и создать на плоском листе глубокое трехмерное пространство.

Освещение предметов может быть концентрированным или рассеянным. Прямой свет солнца или лампы дает концентрированное освещение. Направленный свет, проходящий через среду, рассеивающую световые лучи, создает рассеянное освещение. Когда разница между размером предмета и расстоянием от него до источника света незначительна, то необходимо учитывать радиальное распространение све­товых лучей (рис.133). В тех случаях, когда величина освещаемого предмета значительно меньше рас­стояния от него до источника света (все предметы на земле по отношению к солнцу и предметы, разме­ры которых во много раз меньше расстояния до лампы), лучи света принимаются параллельны и (рис.134).

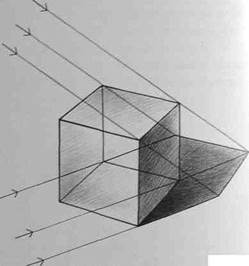Рис.133

Рис.134

Освещенность поверхности предмета зависит от силы источника света, расстояния от источника све­та до поверхности предмета, а также от угла падения световых лучей на эту поверхность. В этом легко убе­диться, наблюдая за изменением положения листа белой бумаги по отношению к лампе. Так из двух листов, расположенных параллельно на разном расстоянии от лампы, лист, расположенный ближе к источнику света, освещен сильнее, а расположенный дальше - слабее. Поворачивая лист бумаги под разными углами к лучам света, мы заметим, что чем более перпендикулярно падают световые лучи на поверхность предмета, тем

светотеневой рисунок простых геометрических тел

сильнее она освещена, а чем острее угол падения лучей, тем менее освещенной становится поверхность

Основные светотеневые закономерности можно рассмотреть и усвоить на двух полосках плотной бе­лой бумаги, согнутой в S-образную ленту. Первая полоска (рис.135) согнута таким образом, что общая фор­ма складывается из ряда расположенных под углом друг к другу плоскостей, вторая полоска (рис 136) име­ет мягкие изгибы Осветив обе полоски параллельными лучами света от солнца или отдаленной лампы прос-ледим на них расположение всех элементов светотени.

Так как различные участки поверхности располагаются под разными углами к световым лучам, то они имеют и различную освещенность. Эту различную освещенность поверхности условимся называть: «самое светлое место», «свет», «полусвет», «полутень», «собственная тень», «падающая тень» и «рефлекс»

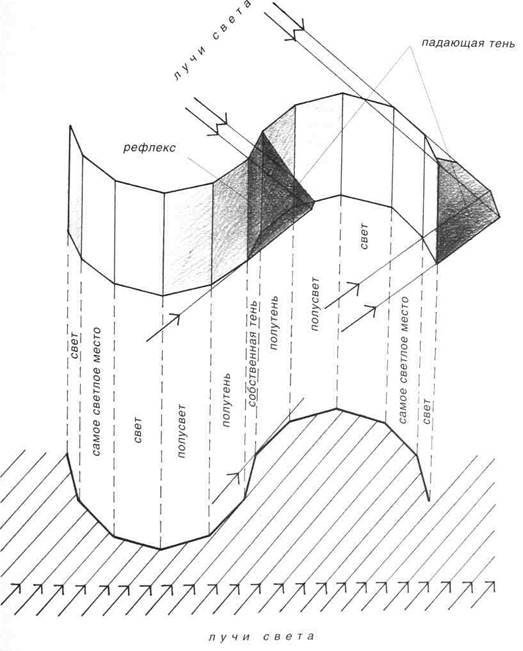
Рис.135

52 глава III

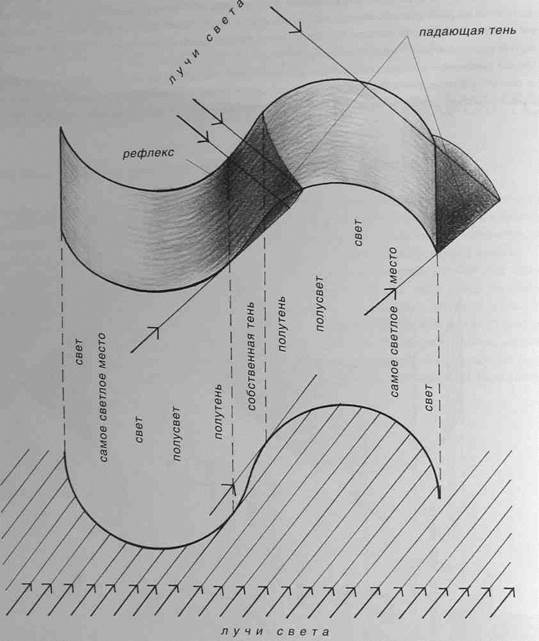
Рис.136

Самое светлое место располагается там, где лучи света падают перпендикулярно к поверхности. Свет помещается рядом с самым светлым местом по обе стороны от него. Полусвет располагается рядом со светом на поверхности, еще более отвернутой от света. Полутень следует за полусветом, занимая по­верхность, освещаемую лучами света, падающими под острым углом.

Рефлекс - это действие на поверхность отраженных лучей. Помимо прямого света, на поверхности предметов падают лучи света, отбрасываемые от других предметов или отраженные одними частями пред­мета на другие его части. Явление рефлекса может наблюдаться как в свету, так и в тени однако в тени оно заметнее. Высветление отраженным светом теней более выражено на изогнутых поверхностях чем на плос­ких, так как в этом случае меняется не только расстояние от рефлексирующей поверхности до теневой, но и угол падения отраженных лучей на теневую поверхность.

светотеневой рисунок простых геометрических тел

Собственная тень лежит на поверхностях, отвернутых от света, на них не попадают прямые лучи от источника света. Границу между освещенными и находящимися в тени поверхностями предмета, принято на­зывать «линией собственном тени». Она определяется световыми лучами, идущими касательно поверхнос­ти предмета, и зависит от формы предмета и направления лучей света.

Падающая темь располагается на повернутых к свету поверхностях, если другие поверхности пре­пятствуют попаданию на них прямых лучей от источника света. Ее сила зависит от расстояния до пред­мета, отбрасывающего тень, от положения поверхности, воспринимающей тень, а также от воздействия отраженного света. Границу падающей тени называют «линией падающей тени». Линия падающей тени зависит от линии собственной тени на предмете и от формы поверхности, на которую падает тень.

Рассматривая изменения освещенности световых поверхностей на S-образных лентах бумаги, оп­ределим существенную разницу в переходах световых градаций на граненой полоске и на мягко изогну­той. На первой - каждая грань имеет ясно выраженную освещенность, четко ограниченную ребрами пе­регибов, на второй - освещенность плавно меняется по мере поворота поверхности, и мы не видим гра­ниц между бесконечным количеством светотеневых градаций.

На граненой полоске линия собственной тени проходит по ребру изгиба и четко отделяет световую поверхность от теневой. На мягко изогнутой полоске линия собственной тени проходит по образующей в месте касания лучей света к изогнутой поверхности и, хотя теоретически она и разделяет свет и тень, резкой границы между ними мы не увидим.

Расположение на предмете градаций светотени: самого светлого места, света, полусвета, полуте­ни, линии собственной тени, собственной тени, рефлекса и падающей тени обусловлено формой предме­та и его положением по отношению к источнику света. Зрительное восприятие светотеневых градаций зависит, кроме того, и от местоположения зрителя по отношению к рассматриваемому предмету.

При перемещении точки зрения относительно освещенного предмета, линии собственной тени, разграничивающие свет и тень, не меняют своего места на предмете, теневые поверхности могут полу­чать самые незначительные изменения. Освещенные поверхности, отражающие большое количество световых лучей, могут зрительно меняться довольно сильно. Например, достаточно большая освещен­ная цилиндрическая поверхность будет казаться светлее в том месте, от которого в глаз попадает боль­ше отраженных поверхностью лучей, идущих от источника света, т.е. там, где угол падения лучей будет равен углу их отражения от поверхности в глаз зрителя. Это место принято называть относительно светлое место.

На глянцевых поверхностях относительно светлое место наиболее выражено и воспринимается как яркий блик. По той же причине, из двух одинаково освещенных граней куба, та покажется глазу светлее, которая больше развернута к зрителю.

Восприятие светотени зависит и от расстояния между зрителем и предметом. С одной стороны, это объясняется разрешающей способностью глаза по-разному воспринимать один и тот же предмет на раз­ных расстояниях, с другой - воздушной средой, находящейся между глазом и предметом, задерживающей и рассеивающей отраженные от предмета лучи света. По мере удаления предметов от зрителя, контраст между освещенными и теневыми поверхностями уменьшается: интенсивность светов падает, тени высвет­ляются. Это явление, называемое воздушной перспективой, позволяет воспринимать глубину простран­ства и передавать ее на плоскости картины.

Все многообразие светотеневых градаций от самого светлого до самого темного передается в ри­сунке тоном, являющимся одним из важных изобразительных средств. Изобразительные материалы ри­сунка - даже самая белая бумага и самый черный карандаш - весьма ограничены в своем диапазоне, они не в состоянии показать абсолютной силы светлого и темного, существующей в природе. Поэтому в ри­сунке приобретают особое значение не абсолютная сила того или иного тона на бумаге, а отношения си­лы тонов между собой и их взаимное соподчинение.

Главное отношение, которое нужно взять,- это тональное отношение света и тени. Это отношение будет самым контрастным, ему должны быть подчинены другие элементы светотени: нюансы в свету и те­ни. Только при взаимном соподчинении этих отношений можно добиться цельности рисунка, наиболее полно выявить форму и пластику изображаемого предмета. Объективные закономерности распределе­ния светотени и особенности субъективного ее восприятия легче проследить и усвоить на простых геометрических телах.

54 глава III

15. Светотеневой рисунок куба, четырехгранной и шестигранной призм.

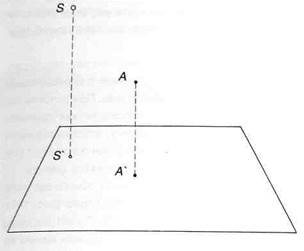
Рассмотрите куб, стоящий на горизонтальной поверхности и освещенный одним близким источником света лучи от которого распространяются радиально. Источник света расположен таким образом, что из трех видимых нам граней куба одна находится в тени, две - в свету. Изобразите на листе это положение ку­ба, источник света (S) и проекцию источника света на плоскость (S') (рис.137).

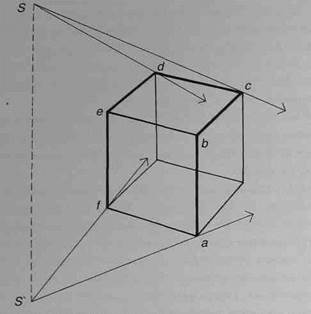
Рис.137

Граница между светом и тенью на кубе определяется лучами, касательными к его поверхности, и про­ходит по ребрам, образующим ломаную линию собственной тени. Обозначим ее на рисунке a-b-c-d-e-f. Линия падающей тени образуется пересечением лучей света, идущих касательно поверхности куба с поверх­ностью, на которую падает тень. То есть линия падающей тени есть тень от линии собственной тени, - в дан­ном случае от ломаной a-b-c-d-e-f. Изобразить падающую тень от куба нам помогут примеры построе­ния падающей тени от точки и прямой на плоскость.

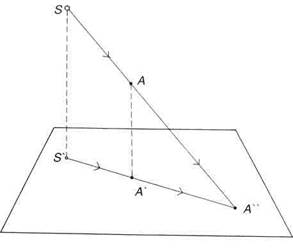
Для построения падающей тени от точки необходимо задать точку (А), ее проекцию на плоскость А), источник света (S) и его проекцию на плоскость(S') (рис.138). Падающая тень от точки лежит на пересечении луча, идущего от источника света через эту точку с проекцией этого луча на плоскость, воспринимающую па­дающую тень. Проведите луч из источника света S через точку А и луч из проекции источника света S' ч рез проекцию точки А'. Точка А" на их пересечении является тенью точки А на данную плоскость (рис.139).

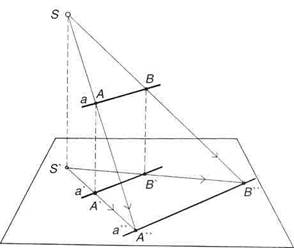
Падающая тень от прямой а (рис.140) на плоскость есть прямая а", найти положение которой можно, построив тени от любых двух точек (А и В), лежащих на этой прямой (рис.141). Заметим, что если прямая а параллельна плоскости, на которую падает тень, то прямые а, ее проекция на плоскость а' и ее тень а параллельны и сходятся на перспективном рисунке в одной точке (если плоскость горизонтальная, то пря­мая, ее проекция и ее тень сходятся в точке на линии горизонта).

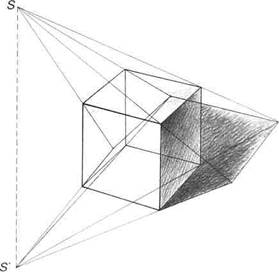
Вернемся к построению падающей тени от куба. Очевидно, что, построив падающие тени от характер­ных точек перелома линии собственной тени и затем, последовательно соединив их прямыми, мы получим ли­нию падающей тени (рис.142). Падающая тень от точки а есть сама точка а, так как она принадлежит плоскос­ти, на которую падает тень. Падающую тень от точки b найдите на пересечении луча из S через точку b с лу­чом из У через проекцию точки b на плоскость (точку а). Обозначьте полученную точку тени от точки b-b ''.

Падающие тени от точек с, d и е найдите аналогично точке b и обозначьте их с", d'' и е". Падающая тень от точки f - сама точка f. Соедините полученные точки а-b" - с"- d" -e"-f прямыми линиями. Это и есть линия падающей тени от куба на плоскость. Обратите ваше внимание на параллельность отрезков b-c,c-d и d - е соответственно отрезкам Ь" - с", с"- d" и d" - е". Это объясняется, как вы уже знаете, тем, что от­резки b - c, c-d и d-e параллельны плоскости, воспринимающей падающую тень от них.

светотеневой рисунок простых геометрических тел 55

Рис.138

Рис.139

 

 

 

Рис.140

Рис.141

 

Рис.142

Рис.143

56 глава III

Изучая в натуре собственные и падающие тени окружающих нас предметов, вы легко заметите, что в любом случае, если линия собственной тени незамкнута и имеет конечные точки, эти же точки являются конечными и для линии падающей тени. Так, линия падающей тени от куба и линия его собственной тени имеют общие точки а и f.

В определенных таким образом освещенных и теневых поверхностях куба тональное решение будет следующим (рис.143). Грань, находящаяся в собственной тени, будет темнее на границе с освещенными поверхностями. Удаляясь от источника света и от зрителя, она высветляется рефлексами. При условии ос­вещения куба точечным источником света, падающая тень на горизонтальную плоскость, как правило, несколько темнее собственной и осветляется при удалении от зрителя и от предмета, отбрасывающего тень. Из двух освещенных граней куба светлее будет та, на которую лучи света от источника падают под большим углом. Удаляясь от зрителя и источника света, освещенные поверхности становятся темнее.

Рис.144

Любой выбранный для тонального рисунка карандаш создает тональную шкалу от самого светлого тона (белого листа) до самого темного, соответствующего наибольшему нажиму на карандаш (рис. 144). В зависимости от характера рисунка, мы можем использовать всю шкалу или ее часть. В светотеневом рисунке белой гипсовой натуры обычно для самого сильного тона шкалы применяют средний нажим на карандаш мягкости В или 2В.

Рис.145

Изобразите такую шкалу - полосу, состоящую из десяти квадратов, отличающихся друг от друга по силе тона. Следите за тем, чтобы каждый квадрат отличался от предыдущего и последующего на едини­цу тона (рис.145). Таким образом, вы добьетесь равномерности перехода от светлого к темному.

Пять более светлых тонов используйте в рисунке для передачи тональных отношений в свету, пять рду" гих более темных - для проработки теневых поверхностей. В зависимости от выбранного вами самого силь­ного тона рисунок будет нюансным или контрастным. Помните, что самое темное место в свету должно быть светлее самого светлого места в тени. Соблюдение этого правила поможет вам добиться наиболее вырази­тельной передачи светотеневых отношений в рисунке как с натуры, так и по представлению.

светотеневой рисунок простых геометрических тел

Светотеневой рисунок куба.

Начните рисунок с определения освещенных и теневых поверхностей, линии собственной тени и линии падающей тени (рис.146).

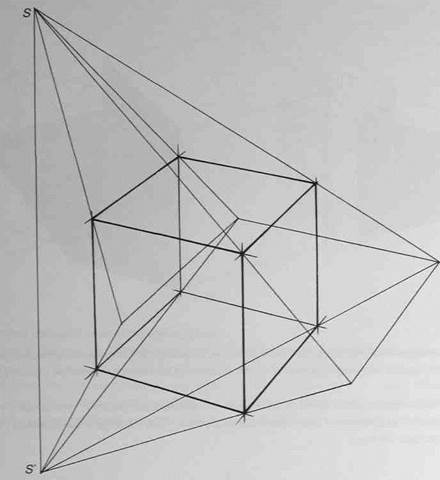
Рис.146

Следующая стадия - отделение «света» от «тени». Прокройте штрихом несколько раз теневые по­верхности (рис.147).

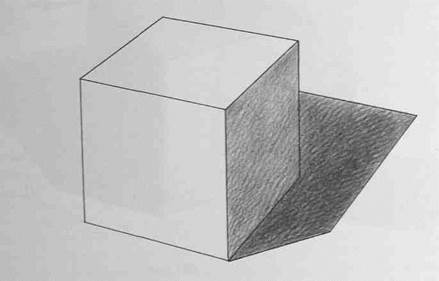
Рис.147

глава III

Продолжите работу «в тени». Усильте собственную тень по направлению к источнику света, падающую тень - к зрителю и кубу (рис.148).

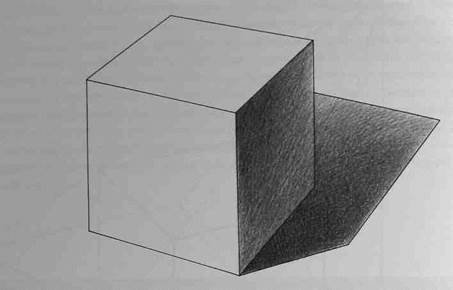
Рис.148

И лишь проработав тени в достаточной степени, переходите к освещенным поверхностям (рис.149), помня о том, что самое насыщенное тоном место в свету не должно быть темнее самых светлых рефлек­сов в тени.

Предлагаемая последовательность ведения светотеневого рисунка «от тени в свет» неслучайна, с ча позволяет избежать традиционной для начинающих ошибки: когда теневые и освещенные поверхности ста­новятся одинаковыми по тону.

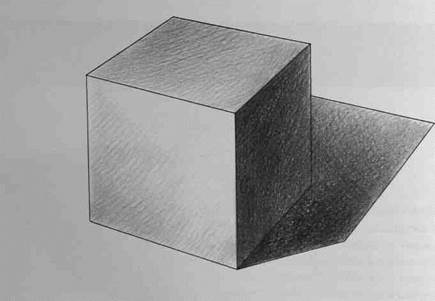
Рис.149

светотеневой рисунок простых геометрических тел 59

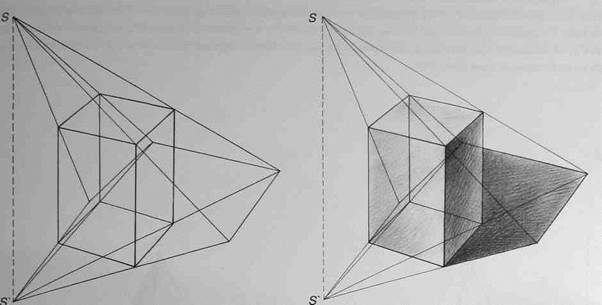
Светотеневой рисунок четырехгранной призмы ведется в той же последовательности, что и рису­нок куба (рис.150 и 151).

 

 

Рис.150

Рис.151

Светотеневой рисунок шестигранной призмы.

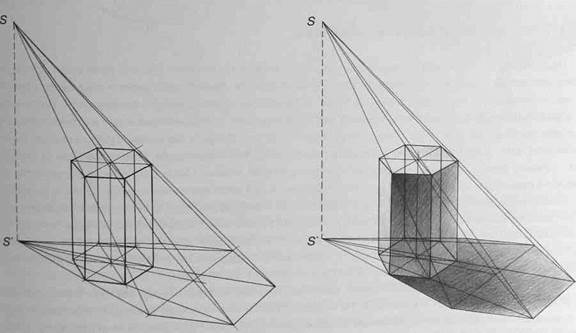
Линия собственной тени на шестигранной призме, как и на кубе, определяется касанием лучей све­та к ее ребрам, образуя ломаную границу между освещенными и теневыми поверхностями. Линия пада­ющей тени находится путем построения падающих теней от характерных точек переломов линии собственной тени (рис.152). Увеличение количества граней шестигранной призмы по сравнению с кубом да­ет нам возможность различить большее количество тональных градаций как в свету, так и в тени (рис.153).

 

 

Рис.152

Рис.153

глава III

16. Светотеневой рисунок пирамиды.

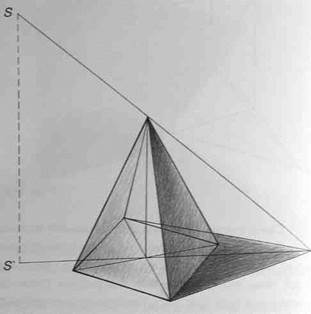
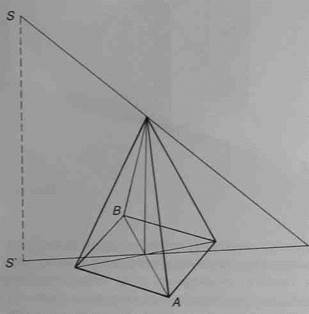
Определить линию собственной тени пирамиды и линию ее падающей тени вам поможет следую-щее построение. Найдите точку падающей тени от вершины пирамиды (рис.154). Проведите из этой точ­ки лучи к основанию пирамиды, как бы охватывающие его и касающиеся двух его вершин (точки А и В). Эти лучи являются линией падающей тени, а ребра пирамиды, идущие от точек А и В к вершине - лини­ей ее собственной тени (рис.155).

 

 

Рис.154

Рис.155

17. Светотеневой рисунок цилиндра.

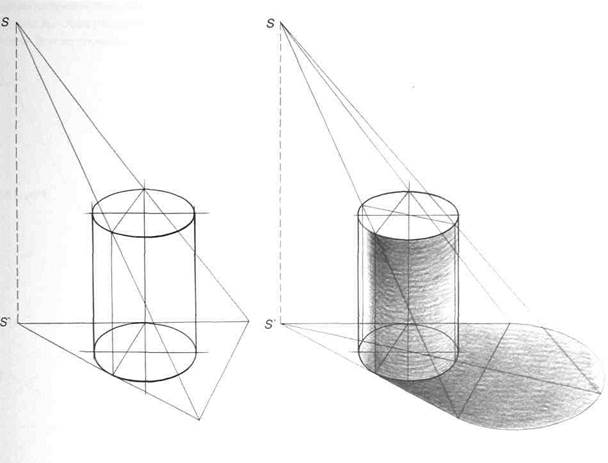
При таком расположении источника света, как показано на рисунке 156, его лучи будут освещать верхнее основание стоящего цилиндра и боковую поверхность. Линию собственной тени будет опреде­лять часть окружности верхнего основания и две образующие цилиндрической поверхности. Положение этих образующих можно определить, проведя две касательные к основанию цилиндра из точки проекции источника света S" на плоскость. Линия падающей тени от стоящего цилиндра будет тенью от линии собственной тени - двух образующих и части окружности верхнего основания. Падающие тени от образу­ющих - прямые линии, принцип построения которых вам уже знаком. Падающая тень от окружности ос­нования на плоскость, ей параллельную, есть окружность, а в перспективном рисунке - эллипс (рис.157).

После определения положения линий собственной и падающей теней для продолжения светотене­вого рисунка необходимо хорошо представлять основные тональные отношения освещенных и теневых по­верхностей цилиндра. Как вы уже знаете, на поверхности, состоящей из ряда плоскостей, каждая грань имеет свою четко выраженную освещенность, ограниченную ребрами. На изогнутой цилиндрической по-верхности, не имеющей граней, переход от света к тени будет постепенным.

Линия собственной тени - самое темное место на цилиндре. Контраст между светом и тенью усилива­ется ближе к источнику света и к зрителю. На теневую поверхность цилиндра действуют отраженные лучи света, вызывая постепенное ее высветление по мере удаления от линии собственной тени (рефлекс). Само светлое место цилиндрической поверхности располагается вдоль образующей, лежащей на пути луче. проходящих через ось цилиндра. При малом радиусе кривизны поверхности цилиндра это светлое мест

светотеневой рисунок простых геометрических тел 61

приближается к линии, при больших радиусах оно имеет некоторую ширину. На освещенную часть цили­ндрической поверхности лучи света падают все под более острым углом по мере поворота поверхности от источника света. Между самым светлым местом и линией собственной тени на боковой поверхности цилиндра располагаются полусвета и полутени, постепенно утемняющиеся от света и мягко переходящие в тень. Степень интенсивности этого перехода зависит от кривизны поверхности: чем меньше ее радиус, тем переход совершается быстрее, при большем радиусе эти же светотеневые градации располагаются на большем протяжении.

 

Рис.156 Рис.157

Рассматривая цилиндр с разных точек зрения, мы заметим, что линия собственной тени не меняет свое­го места на цилиндрической поверхности. Неизменными остаются также области собственной тени и рефлекса. Однако освещенная поверхность цилиндра существенно меняется. При перемещении точки зрения вокруг цили­ндра воспринимаемое глазом относительно светлое место также перемещается: оно располагается в том месте поверхности, которое отражает наибольшее количество лучей света в глаз зрителя. При этом воспринимаемая тазом область полусветов и полутеней, заключенная между перемещающимся относительно светлым местом ^и постоянной линией собственной тени, соответственно сжимается или расширяется. Падающая тень от цилиндра усиливается, то есть становится темнее по направлению к цилиндру и зрителю.

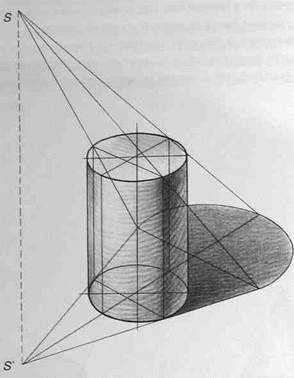
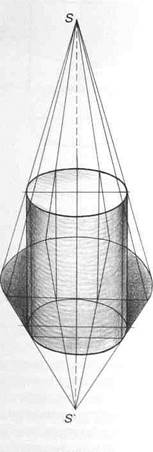
Рассмотрите рис.158,159 и 160, на которых показана светотень на цилиндрах с различным положени­ем источника света.

62 глава III

Рис.158

 

 

Рис.159

Рис.160

светотеневой рисунок простых геометрических тел 63

18. Светотеневой рисунок конуса.

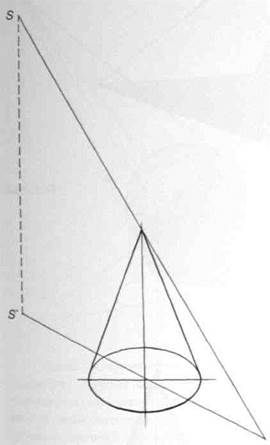
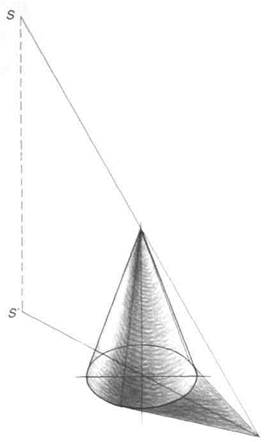
Распределение элементов светотени на конусе имеет некоторые особенности. Когда боковая пове­рхность конуса освещена, линия собственной тени будет проходить по двум образующим, к которым по касательным направлены лучи света от источника. Падающая тень от конуса, а также линия собственной тени строится подобно теням на пирамиде. Сначала найдите падающую тень от вершины конуса (рис.161). Затем проведите из этой точки лучи, касательные к окружности основания. Эти лучи являются линией падающей тени, а образующие, проведенные из точек касания в вершину конуса - линией собственной тени (рис. 162).

При изменении высоты источника света относительно конуса, образующие, по которым проходит ли­ния собственной тени, как бы сдвигаются и раздвигаются, уменьшая или увеличивая область тени. При дос­таточно высоком расположении источника света над конусом, его поверхность оказывается освещенной це­ликом. В этом случае конус не имеет падающей тени.

Рис.161

Рис.162

Как и у цилиндра, линия собственной тени - самое темное место на изогнутой поверхности конуса. Контраст между светом и тенью по мере уменьшения радиуса конической поверхности увеличивается, а зна­чит, на поверхности конуса линия собственной тени будет утемняться к вершине. Отраженный свет высветляет собственную тень. Самое светлое место имеет форму треугольника и располагается вдоль образующей, "ежащей на пути лучей, проходящих через ось конуса.

Рассматривая конус с различных точек зрения, заметим, что воспринимаемое глазом относительно светлое место и области полусветов и полутеней перемещаются подобно тому, как это наблюдалось на цилиндре, а области собственной и падающей теней остаются неизменными. Падающая тень от конуса будет усиливаться по направлению к конусу и зрителю.

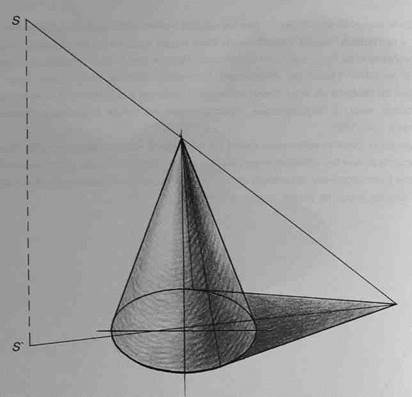
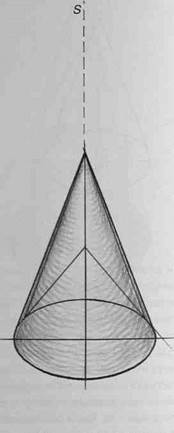
На рисунках 163, 164 и 165 показано распределение светотени на конусах с различным положением

источника света.

64 глава III

 

Рис.163

Рис.164

Рис.165

светотеневой рисунок простых геометрических тел 65

19. Светотеневой рисунок шара.

Линия собственной тени шара, освещенного одним источником света, проходит по окружности, точки которой определятся касанием лучей света к поверхности шара. Плоскость этой окружности перпендикуляр­на лучу света, идущему от источника света через центр шара (рис.166). Падающая тень от шара на плоскость всегда будет тенью от окружности. Тень от окружности - эллипс, который и в перспективном рисунке изобра­жается в виде эллипса. Построение падающей тени от шара по своему принципу не отличается от построения падающих теней от других геометрических тел. Сложность заключается в том, что и линия собственной тени на шаре, и ее проекция на плоскость, необходимые для построения падающей тени, рисуются по ощущению и не могут служить основой для точного построения. Поэтому зная, что падающая тень от шара на плоскость всегда имеет форму эллипса, обычно ее так и изображают - в виде эллипса, определяя его размер при помо­щи двух касательных к шару лучей и направление в зависимости от положения источника света (рис.167).

Самое темное место на поверхности шара - граница света и тени, она становится еще темнее ближе к зрителю. Теневая поверхность шара высветляется отраженным светом. Самое светлое место на поверхности шара всегда располагается вокруг точки пересечения ее лучом света, идущим через центр ша­ра. Это самое светлое место может быть больше или меньше в зависимости от кривизны поверхности шара. От самого светлого места освещенность постепенно уменьшается во всех направлениях, переходя через зо­ны полусветов и полутеней в собственную тень. Как и в примере с другими геометрическими телами, отно­сительно светлое место на шаре характеризуется наибольшим количеством лучей света, отраженных пове­рхностью шара в глаз зрителя, следовательно, его расположение меняется в зависимости от положения зри­теля. Линии собственной и падающей теней, а также зона рефлекса остаются неизменными при изменении точки зрения. Падающая тень от шара становится темнее по направлению к зрителю и к самому шару.

Рассмотрите рисунки 168,169 и 170, на которых показано распределение элементов светотени на ша­рах с различным положением источника света.