Соответствие круга и квадрата в перспективе.

Анализируя различные положения квадрата и окружности относительно точки зрения и линии горизонта а также правила их изображения в перспективе легко обнаружить общие закономерности. Геометричес­кая связь этих фигур определяется тем, что вокруг любой окружности можно описать квадрат, а также в лю­бой квадрат можно вписать окружность.

Как вписать окружность в квадрат?

Рассмотрите рисунок 48. Квадрат и вписанная в него окружность имеют общий центр - точку пересече­ния диагоналей квадрата. Окружность касается сторон квадрата в точках 1,2,3,4.Точки касания делят стороны квадрата пополам. Для того чтобы изобразить вписанную в квадрат окружность (в перспективном рисунке - эл­липс) необходимо определить положение осей эллипса и найти точки, задающие его размеры (точки 1 - 4).

Рис.48

Горизонтальный квадрат.

Найдите точки касания на перспективном рисунке горизонтально расположенного квадрата (рис.49): для этого через точку пересечения диагоналей проведите прямые, параллельные сторонам квадрата и ухо­дящие с ними в одну точку схода.

Окружность, лежащая в горизонтальной плоскости, изображается в виде эллипса с вертикальной и го­ризонтальной осями. Проведите через точку пересечения диагоналей вертикальную линию - малую ось эллип­са. Большая ось эллипса перпендикулярна малой оси и проходит через точку, смещенную от пересечения ди­агоналей квадрата (центра окружности) ближе к зрителю (рис.50). Таким образом, мы получили две оси эл­липса и четыре точки, определяющие его габариты. Продолжите рисунок: сначала легкими движениями ка­рандаша наметьте эллипс, затем уточните линию, добиваясь того, чтобы она действительно касалась сторон квадрата в точках 1,2,3,4. Проверьте симметричность полученного эллипса относительно его осей (рис. 51).

Рис.49

Рис.51

перспективный рисунок простых геометрических тел

Вертикальный квадрат.

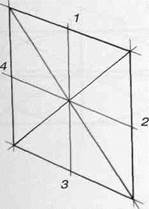
При вертикальном положении квадрата точки 1,2,3,4 найдите, как и в предыдущем примере: прове­дите через точку пересечения диагоналей квадрата прямые, параллельные его сторонам (рис.52). Несколь­ко сложнее определить направление осей эллипса. Для решения этой задачи представьте, что изображаемый нами эллипс является основанием цилиндра, лежащего на горизонтальной плоскости (рис. 53). Ось цилиндра всегда перпендикулярна большой оси эллипса основания и совпадает с его малой осью. Проведите ось ци­линдра через точку пересечения диагоналей квадрата. Ее направление можно найти, опираясь на знание и опыт рисования куба, или взять с натуры, если таковая имеется. Таким образом, мы определили положение малой оси эллипса. А большая ось будет ей перпендикулярна и пройдет через точку, смещенную от пересе­чения диагоналей - центра окружности - ближе к зрителю (рис.54). На двух осях и по четырем точкам сна­чала наметьте эллипс легкими линиями, а затем уточните рисунок (рис.55).

Заметим, что эллипс, вписанный в квадрат, часто получается несимметричным относительно осей, а потому его приходится уточнять и, как следствие, изменять очертания квадрата. В этом случае работа идет как бы методом последовательных приближений и исправлений, что трудно и долго. Часто на рисунках остаются не вполне правильные квадраты и не вполне правильные эллипсы, а лишь фигу­ры, близкие к ним. Правильный эллипс нарисовать легче, чем построить правильный квадрат в перспекти­ве, поэтому задачу грамотного изображения квадрата современная методика рисования предлагает решать с помощью эллипса, вокруг которого описывается квадрат.

Рис.52

Рис.53

Рис.54

Рис.55

глава II