Вертикальная окружность.

Рассмотрим пример, когда перед рисующим ставится задача описать вокруг горизонтального цили­ндра четырехгранную призму, лежащую на горизонтальной плоскости. При таком положении цилиндра ок­ружности его оснований будут вертикальными.

Начните построение с ближнего к нам основания. Описанный вокруг него квадрат имеет две верти-

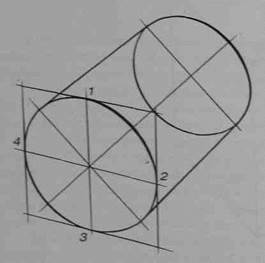
кальные стороны, которые остаются вертикальными и на перспективном рисунке. Проведите две вертикаль­ные касательные к эллипсу и найдите точки 2 м 4. Прямая, соединяющая их. будет иметь горизонтальное нап­равление (рис.62). Теперь проведите вертикальную прямую через центр окружности (точку, смещенную от­носительно центра эллипса дальше от зрителя) и найдите точки 1 и 3 (рис.63). Прямые, касательные к эллип­су в этих точках, параллельны прямой 4-2, уходят с ней в одну точку схода на горизонте и определяют по­ложение двух горизонтальных сторон квадрата (рис.64). Второе основание призмы мы получим путем анало­гичных построений. Соединив соответствующие вершины ближнего и дальнего основания, завершите рису­нок призмы, описанной вокруг цилиндра (рис.65). Проверить правильность рисунка можно, проследив парал­лельность длинных сторон боковых граней призмы: они должны уходить в одну точку схода с осью цилинд­ра и его образующими.

Для закрепления этого материала мы рекомендуем проделать подобные построения несколько раз. Свободное владение этими навыками позволит вам перейти к перспективному изображению более сложных геометрических тел: конуса, шестигранной призмы, шара.

Риc.63

 

 

Рис. 64

Рис.65

перспективный рисунок простых геометрических тел

Рисунок конуса.

Конус является телом вращения, получить которое можно путем вращения прямоугольного треуголь­ника вокруг одного из катетов. В основании конуса лежит окружность. Ось конуса перпендикулярна основа­нию и соединяет центр окружности основания с вершиной конуса. Пропорции конуса определяются отноше­нием диаметра основания к его высоте, в нашем примере -1:1,5 (рис.66).

Рис.66

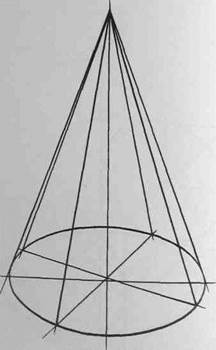
Построение вертикального конуса в перспективе начните с эллипса основания. Продолжите малую ось эллипса и на полученной прямой от центра окружности отложите высоту конуса (рис.67). Из полученной точ­ки - вершины конуса - проведите две касательные к эллипсу (рис.68).

 

 

Рис.67

Рис.68

32 глава II

 

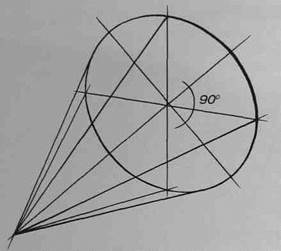
Рис.69

Изображая конус в произвольном положении, помните, что его ось всегда перпендикулярна большой оси эллипса основания (рис.69). Как и в случае с другими геометрическими телами, вам следует сделать нес­колько рисунков конуса в перспективе в различных положениях с натуры, а затем по представлению.

Сечения конуса плоскостями, параллельными плоскости его основания - окружности разного диамет­ра, в перспективном рисунке - эллипсы, с разной длиной большой оси и разным раскрытием в зависимости от положения плоскости сечения (рис.70). Сечение конуса плоскостью, перпендикулярной плоскости его ос­нования и проходящей через вершину конуса - равнобедренный треугольник, основание которого равно ди­аметру окружности основания конуса, а высота равна высоте конуса (рис.71).

 

 

Рис.70

Рис.71

перспективный рисунок простых геометрических тел

 

Рис.72

 

Рассекая конус плоскостями, перпендикулярными плоскости основания, но не проходящими через вер­шину конуса, можно получить разные по высоте гиперболы (рис.72). На построении таких сечений мы оста­новимся подробнее.

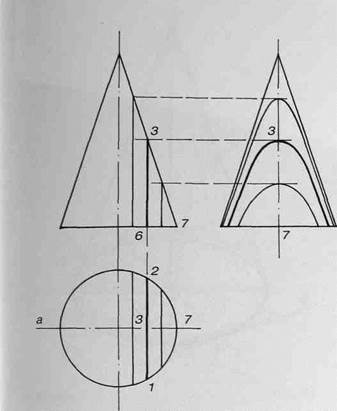
На перспективном рисунке конуса сначала задайте положение секущей плоскости: проведите линию пересечения секущей плоскости с плоскостью основания - прямую 1-2 (рис.73). Точки 1 и 2 - характерные точки сечения, определяющие направление ветвей гиперболы.

Затем найдите верхнюю точку гиперболы (т.З), лежащую на пересечении вертикали 6 - 3 и образую­щей 7-3. Для определения положения точек 6 и 7 постройте перпендикуляр к прямой 1-2 через центр ок­ружности - прямую а, пересечение которой с прямой 1 -2 и эллипсом основания даст нам искомые точки 6 и 7. Направление прямой а определите при помощи касательных. Для этого проведите через центр окружнос­ти прямую, параллельную прямой 1 - 2 и обозначьте точки ее пересечения с эллипсом как 4 и 5. Прямые b и с, касающиеся эллипса в точках 4 и 5, перпендикулярны диаметру 4 -5, а значит и прямой 1-2 (рис.74). Теперь проведите через центр окружности прямую а,-параллельную прямым Ь и с (уходящую с ними в од­ну точку схода) - это и есть искомый перпендикуляр к прямой 1-2. Обозначьте точки 6 и 7 (рис.75). Восста­новите перпендикуляр из точки 6 и проведите образующую из точки 7 в вершину конуса - на пересечении этих прямых найдем точку 3 - верхнюю точку гиперболы (рис.76).

Таким образом мы получили три точки {1, 2 и 3), определяющие положение линии сечения. Теперь проведем три вспомогательные прямые, которые позволят нам точнее изобразить гиперболу. Горизон­тальная прямая, параллельная 1 - 2 и проходящая через точку 3, касается в этой точке гиперболы и оп­ределяет ее очертание в верхней части. Две прямые, проведенные через точки 1" и 2\ параллельные об­разующим конуса из точек 4 и 5 определяют характер ветвей гиперболы. Ветви гиперболы должны пос­тепенно приближаться к этим прямым, но не пересекать их (рис.77). Изобразите гиперболу. Проверьте симметричность полученной кривой относительно вертикальной оси 3-6 (рис.78). Постройте несколько таких сечений, параллельных друг другу, проследите за изменением характера гиперболы при движении секущей плоскости от края к вершине конуса: ближнее к краю сечение подобно верхней части сечения, расположенного ближе к вершине (рис.79).

34 глава II

 

 

Рис.73

Рис.74

 

 

 

Рис.75

Рис. 76

перспективный рисунок простых геометрических тел 35

 

 

Рис.77

Рис.78

Рис.79

36 глава II

Рисунок шестигранной призмы.

В основании шестигранной призмы (шестигранника) лежат правильные шестиугольники. Сторона пра­вильного шестиугольника равна радиусу описанной окружности (рис.80). Исходя из этого, легко начертить шестиугольник: изобразите окружность при помощи циркуля, затем из крайних точек любого диаметра сде-лайте засечки на окружности, не меняя раскрытия циркуля (рис.81). Полученные таким образом шесть точек являются вершинами шестиугольника.

Рис.81

Рис.80

Рассмотрите подробнее эту фигуру на рис.82. Обозначьте вершины шестиугольника цифрами от од­ного до шести и соедините точки 1 и з, 4 и 6, как показано на рисунке. Прямые 1 - 3 и б - 4 вместе с точкой центра окружности делят диаметр 5 - 2 на четыре равных отрезка. Противоположные стороны шестиуголь­ника параллельны друг другу и прямой, проходящей через его центр и соединяющей две вершины (напри­мер, стороны 6-1 и 4-3 параллельны прямой 5-2). Эти наблюдения помогут вам построить шестиугольник в перспективе, а также проверить правильность этого построения.

Рис,82

Рис.83

Существует несколько способов построения шестиугольника в перспективе (рис.83): на основе описан­ной окружности; на основе прямоугольника; на основе квадрата. На основе описанной окружности. Рассмотрите рисунок 84.

Рис.84

перспективный рисунок простых геометрических тел