Метод слоя конечной толщины

Среди поверхностных явлений наибольший практический интерес представляет адсорбция. Адсорбцией называется процесс перераспределения компонентов гетерогенной системы между её фазами и поверхностным слоем. Фазы гетерогенных систем могут находиться в любом агрегатном состоянии. Поэтому адсорбция может происходить на границе раздела жидкости и газа, двух ограниченно смешиваемых жидкостей, жидкости и твёрдого тела, твёрдого тела и газа.Адсорбция на границе раздела жидкость-газ представляет собой процессперераспределения компонентов раствора между его объёмом и поверхностнымслоем

При изучении адсорбции из растворов на границе раздела жидкость-газ используется теория поверхностных явлений Гиббса и теория, основанная на представлении о межфазной границе как о неоднородном слое определённого объёма и толщины. Термодинамическая теория плоского поверхностного слоя, основанная на этих представлениях, разработана Гуггенгеймом. Она получила название метода слоя конечной толщины.

В теорииГиббса состав поверхностного слоя оценивается величиной поверхностного избытка N ^S, представляющего собой разность количества вещества, содержащегося в реальной N_p и идеализированной N_ид системах:

N^S= N_р - N_ид (3.1)

В поверхностном слое реальной системы концентрация компонентовизменяется по некоторому закону. На рисунке 3.1 для простоты показаназависимость концентрации вещества от координаты х, отсчитанной вдольнормали к поверхности, в однокомпонентной гетерогенной системе, состоящей из жидкости и её насыщенного пара.

В идеализированной системе (рисунок 3.1б) концентрация постоянна в пределах каждой фазы и изменяется скачком на так называемой

разделяющей поверхности(РП). Поверхностный избыток N^S равен

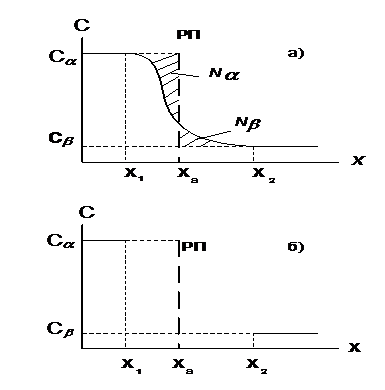
Рисунок 3.1 - Изменение концентрации компонента в реальной (а) и

идеализированной (б)однокомпонентных системах.

 

алгебраической сумме площадей N _α^S и N _β^S, показанных на рисунке 3.1 штриховкой (предполагается, что площадь поверхности жидкости равна 1м²). При смещении разделяющей поверхности в пределах поверхностного слоя поверхностный избыток N ^Sизменяется как по модулю, так и по знаку; при X _S = X₁ N^S > 0, а при X_S = X₂ N^S < 0.

Аналогично поверхностному избытку N^S в теории Гиббса определяютсяразличные экстенсивные термодинамические функции поверхностногослоя.Внутренняя энергия поверхностного слоя U ^S, например, определяетсявыражением следующего вида:

U ^S = U_p– U_ид (3.2)

В теории Гиббса показано, что уравнение, объединяющее 1 и 2 началатермодинамики, для поверхностного слоя многокомпонентной

открытой системы может быть записано следующим образом:

 

dU^S= TdS^S + σdA + 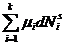(3.3)

где S^S = S_р – S_ид – энтропия поверхностного слоя,

σ - поверхностное натяжение,

А - площадь межфазной поверхности,

μ_i - химический потенциал i -го компонента,

R – газовая постоянная,

Т – абсолютная температура.

Математическими преобразованиями, применяемыми в общем курсе термодинамики, на основе уравнения (3.3) получено адсорбционное уравнение Гиббса: S^SdT + Adσ + ∑N_i^Sdμ_i= 0 (3.4)

При T = const из уравнения (3.4) получается уравнение изотермы адсорбции Гиббса: 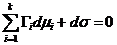(3.5)

где Г_i= N^S_i / A – удельная адсорбция i - го компонента.

Для двухкомпонентного раствора (к = 2) уравнение (3.5) можно записатьв следующем виде:

Г ₁ dμ ₁ + Γ ₂ dμ ₂ + dσ = 0, (3.6)

где μ_i= μ_{0 i}+ RTlna_i– химический потенциал i - того компонента

раствора,

μ_{0 i} - его стандартный химический потенциал,

a_i = γ_i^. х_i – активность i - того компонента раствора,

х_i и γ_i – его концентрация (в молярных долях) икоэффициент

активности, соответственно.

Из величин, входящих в уравнение (3.6), экспериментально определяется только σ и, следовательно, при произвольном положении разделяющей поверхности Г_i однозначно не определяется. Для того, чтобы обойти эту сложность в расчёте Г_i, разделяющая поверхность фиксируется в таком положении, в котором удаётся исключить из уравнения (3.8) одну из неизвестных величин. Одно из таких положений отвечает условию Г₁ = 0. Длятакого положения разделяющей поверхности уравнение Гиббса имеет следующий вид:

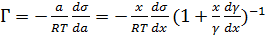(3.7)

В этом выражении индекс «2» опущен и под Г подразумеваетсяудельная адсорбция растворенного вещества. Для идеальных растворов а=х ипоэтому уравнение изотермыадсорбцииимеет следующий вид:

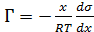(3.8)

Из уравнения (3.8) следует, что удельная адсорбция Г > 0, если при растворении вещества наблюдается понижение поверхностного натяжения (dσ/dC <0), а повышение поверхностного натяжения является признаком отрицательной адсорбции. При положительной адсорбции, как следует из опытных данных, концентрация растворённого вещества в поверхностном слое больше, чем в объёме раствора, а при отрицательной -больше в объёме раствора.

Вещества, понижающие поверхностное натяжение, называютсяповерхностно-активными (сокращённо ПАВ). При смешении двух жидкостей поверхностно-активным компонентом будет жидкость с меньшим поверхностным натяжением.В водных растворах поверхностно-активными являются органические вещества, молекулы которых имеют дифильное строение: содержат полярную группу (-NO₂, -NH₂, -OH, -COOH и др.) и неполярный радикал. Такие молекулы изображаются символом, показанном на рисунке3.2. Кружочком обозначается полярная часть молекул, а прямой (или волнистой) линией - неполярная часть.

Рисунок 3.2 - Символ дифильной молекулы ПАВ.

Из водных растворов положительно адсорбируетсябольшинство

растворимых в воде органических соединений. Положительная адсорбция

изводных растворов объясняется «гидрофобным эффектом».Это понятиевозникло при изучении растворимости неполярных

веществ (типа углеводородов) в воде. Низкая растворимость неполярных веществ в воде объясняется высокой прочностью водородной связи между молекулами воды. Положительную адсорбцию ПАВ можно рассматривать как процесс, обратный растворению: вытеснение неполярной части молекулы из объёма раствора на поверхность. Имеющиеся опытные данные свидетельствуют о том, что между адсорбцией вещества из раствора и его растворимостью в данном растворителе существует следующая связь: чем хуже вещество растворяется, тем лучше оно адсорбируется на поверхности раздела фаз.

Вещества, повышающие поверхностное натяжение и адсорбирующиеся отрицательно, называются поверхностно-инактивными(ПИАВ). Из водных растворов отрицательно адсорбируются соли неорганических кислот и оснований, сахара и первые члены гомологического ряда аминокислот. Отрицательную адсорбцию ионов из растворов электролитов можно объяснить действием «сил изображения», имеющих электростатическую (поляризационную) природу. Ион, расположенный около границы раздела, своим электрическим полем поляризует обе фазы. При этом на границе раздела появляется связанный поляризационный заряд. Его знак и величина зависят от соотношения диэлектрических проницаемостей фаз. Эти силы получили такое название в виду того, что взаимодействие иона со второй фазой формально можно рассматривать как взаимодействие этого иона с фиктивным зарядом-изображением, расположенным по другую сторону от границы на таком же расстоянии от неё, что и реальный заряд. Знак и величина заряда-изображения, а, следовательно, и сила взаимодействия иона, определяются соотношением диэлектрических проницаемостей фаз. В частности к поверхности металла ион притягивается, а от поверхности диэлектрика отталкивается, если диэлектрическая проницаемость среды больше диэлектрической проницаемости этого диэлектрика. Последнее соотношение диэлектрических проницаемостей характерно системе, в которой наблюдается отрицательная адсорбция ионов из водных растворов на границе с газовой фазой (диэлектрическая проницаемость газов ε ≈ 1, а у воды ε = 80). Аналогично иону ведёт себя около границы раздела двух фаз молекула, обладающая постоянным дипольным моментом. Молекулы сахаров и аминокислот в цвиттер - ионной форме имеют большой дипольныймомент (почти на порядокпревышающий дипольный момент молекул воды) ипоэтому адсорбируются,как и ионы, отрицательно.

Для расчета удельнойадсорбции по уравнению Гиббса используетсяполученная экспериментальнозависимость σ = f(х) в табличном или графическом виде. Входящую в уравнения (3.9) и (3.10) производную поверхностного натяжения по концентрации можно найти графическим или численным дифференцированием. Используя эти методы, были получены изотермы адсорбции органических веществ (кислот, спиртов и др.) из водных растворов со следующей характерной особенностью: на изотерме адсорбции имелся максимум.

Наиболее полные данные об адсорбции компонентов раствора на его поверхности можно получить в том случае, если зависимость σ = f(х) известна в аналитическом виде. Среди ряда предложенных формул наиболее известна и цитируема эмпирическая формула Шишковского:

∆σ = σ_o – σ = Bln (1+Aх) (3.11)

где σ_о и σ – поверхностное натяжение растворителя и раствора с

концентрацией х (в молярных долях),

В и А - эмпирические константы.

Растворы, к которым применимо уравнение (3.11), малочисленны. Однако применение этого уравнения совместно с уравнением Гиббса приводит к результатам подкупающе простым в их физической интерпретации.

Действительно, из уравнения (3.11) следует, что

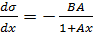. (3.12)

При подстановке в уравнение (3.10) величины производной (3.12) получается уравнение изотермы адсорбции в явном виде:

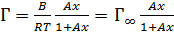(3.13)

где 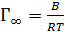– предельная адсорбция – значение Г при Ах → ∞ (рисунок 3.3).

Рисунок 3.3 - Изотерма мономолекулярной адсорбции.

 

Зависимость удельной адсорбции от концентрации типа дробно-линейной функции (3.13) известна, как изотерма мономолекулярной адсорбции. Онабыла полученаЛенгмюромпри теоретическом изучении адсорбции газов наповерхности твёрдых тел.

Представления о мономолекулярном характере адсорбции перенесены на адсорбцию ПАВ на границеразделараствор-газ.Предполагается при этом, что адсорбируемые молекулы ПАВ располагаются на поверхности раствора монослоем. При малых концентрациях раствора молекулы ПАВ в монослое удалены друг от друга на сравнительно большие расстояния. Неполярный радикал в монослое ориентирован под небольшим углом к поверхности. При повышении концентрации происходит заполнение монослоя и при достаточно высокой концентрации, которой соответствует Г = Г_∞ = В/RT, образуется насыщенный мономолекулярный слой (рисунок 3.4).Предполагаетсятакже, что в насыщенном монослоемолекулыПАВориентированы

перпендикулярно поверхности; полярнаягруппа ПАВобращена к полярной фазе (к раствору), а неполярная -кгазовойфазе.

 

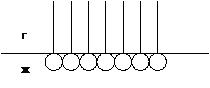
Рисунок 3.4 - Строение насыщенного монослоя из молекул ПАВ.

 

Достоверность гипотезы о мономолекулярном характере адсорбцииможнопроверить, прежде всего, по применимости уравнения (3.11) кэкспериментальной зависимости σ =f(х). Уравнение (3.11) нельзя преобразовать в линейную форму, что затрудняет его проверку и расчёт констант А и В. О применимости формулы Шишковского чаще всего судят по наличию линейного участка на изотерме поверхностного натяжения, построенной в полулогарифмическом масштабе. По начальному и угловому коэффициентам этого участка обычно рассчитываются константы А и В. Обоснованность такой методики определяется заведомо неизвестным условием: Ах >>1.

Константы А и В можно определить по опытным данным с большей достоверностью, если воспользоваться разложением логарифмической функции в степенной ряд следующего вида:

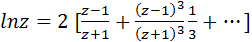(3.14)

Ограничиваясь первым членом разложения, получим

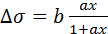, (3.15)

где b = 2B и a = A/2.

Уравнение (3.15) простыми преобразованиями сводится к следующемулинейному виду:

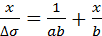(3.16)

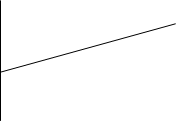
В случае применимости выражения (3.15) график зависимости х/Δσ от х, построенный по опытным данным, должен представлять собой прямую линиюс начальным b₀ и угловым b₁ коэффициентами (рисунок 3.5). Константа а уравнения (3.15), как следует из выражения

 

х/Δσ

Δ (х/Δσ)

b_o

х

Δх

Рисунок3.5 - График для проверки уравнения (3.15).

 

(3.16), равна а = b₁ / b₀, а константа b -величине, обратной угловому коэффициенту b₁= Δ(х/∆σ)/Δх.

Расчёты показывают, чтовеличины Δσ, рассчитанные по

формулам(3.11)и(3.15), отличаютсяменее чем на 1% до ах ≈ 0,2. При большихконцентрациях наблюдается расхождение, характер которого свидетельствует о том, чторезультаты расчётов по формуле (3.15) лучшесовпадают с экспериментальнымиданными, чем полученные по формуле (3.11). Следует заметить, что линейный характер зависимости (3.16) соблюдается и при ах >1.Проверка применимости этого уравнения к экспериментальным изотермамповерхностного натяжения водных и неводных растворов, а также

металлических сплавов дала положительный результат для многих систем.

Не трудно убедиться в том, что уравнению (3.15) соответствует уравнение изотермы адсорбции следующего вида:

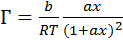(3.17)

Исследование уравнения (3.17) на экстремум показывает, что графикзависимости Г= f (х) представляет собой кривую с максимумом Γ_max = b / 4RT при х = 1/a (рисунок 3.6).Подобного вида изотермы адсорбции былиполучены, в частности, при изученииадсорбции ПАВгомологического рядаалифатическихкислот(от уксусной до

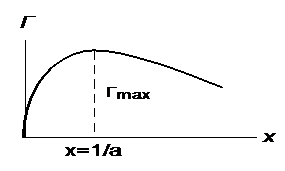
Рисунок 3.6 - Изотерма адсорбции, соответствующая уравнению (3.17).

 

капроновой)и спиртов из водныхрастворов. В этихработах удельная адсорбция рассчитывалась по формуле(3.9), а привычислении производнойповерхностного натяжения по концентрациииспользован численный метод дифференцирования (метод парабол)и поэтому полученные на их основе результаты могут рассматриваться как наиболее достоверные.

При изучении поверхностных явленийкроме метода Гиббса, как отмечалось выше, применяется метод слоя конечной толщины (СКТ). В этом методе неоднородный поверхностный слой рассматривается какотдельная фаза гетерогенной системы, но фаза неавтономная, т.е. не способная существовать самостоятельно. Ей приписывается определённый объём и толщина.

Уравнение, объединяющее 1 и 2 начала термодинамики применительно кповерхностному слою записывается в том же виде, что и для однородных фаз:

dU = TdS + σdA - рdV + ∑ μ_idN_i. (3.18)

Используя математические преобразования уравнения (3.18), аналогичные применяемым в методе Гиббса, получено следующее выражение:

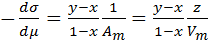(3.19)

где у и х - молярные доли растворённого ПАВ в поверхностном

слое и в объёме раствора, соответственно,

z и V_m – толщина и молярный объёмповерхностного слоя,

соответственно.

Изуравнения (3.19), полученного академиком Русановым А.И., следует, что Г > 0, если у > х и Г < 0, если у < х; при положительной адсорбции концентрация раствора в поверхностном слое больше, чем в объёме, а при отрицательной – больше в объёме. Таким образом, метод слоя конечной толщины даёт физическое объяснение знака удельной адсорбции.

Молярный объём зависит от концентрации раствора. Учитывая малую сжимаемость жидкостей, можно допуститьаддитивность молярного объёма. В этом случае формула (3.19) примет следующий вид:

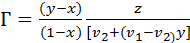(3.20)

где v₂ и v₁ – молярные объёмы растворителя и растворённого

вещества, соответственно,

z – толщина поверхностного слоя.

В работах академика Русанова А.И. был предложен метод оценкиминимальной возможной толщины поверхностного слоя растворов ПАВ,основанный на условииустойчивости поверхностного слоя в отношении его толщины, т.е. способности поверхностного слоя восстанавливать своюравновесную толщину при её случайных изменениях.

Было показано, что признаком устойчивости поверхностного слоя,

вытекающее из условий устойчивости,является симбатное изменение составов поверхностного слоя и сосуществующих фаз вдали от критического состояния. На основании выражения (3.20) и критерия симбатности (dy/dx>0) получена следующая формула, по которой оценивается минимальная возможная толщинаповерхностногослоя:

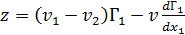, (3.21)

где v = v₂ + (v₁ – v₂) x₁ – молярный объём раствора,

v₁ и v₂ – молярные объёмы ПАВ и растворителя,

Г₁=Г (1- х₁) – удельная адсорбция ПАВ, рассчитанная

относительноэквимолекулярной разделяющейповерхности,

х₁ – молярная доля ПАВ в растворе.

Используя уравнение (3.17) выражению (3.21) можно придать следующий вид:

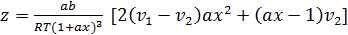(3.22)

Применение «критерия симбатности» показало, что мономолекулярная модель поверхностного слоя для многих бинарных растворов не согласуется с условием устойчивости.

Толщину поверхностного слоя растворов ограниченно растворимых ПАВ можнорассчитать по уравнению (3.20), руководствуясь следующими соображениями. В поверхностном слое таких растворов за счёт положительной адсорбции может достигаться предел растворимости, т.е. может образоваться насыщенный раствор определённой концентрации. Если предположить, что концентрация насыщенного раствора в поверхностном слое равна растворимости данного ПАВ при соответствующей температуре (x_S), по формуле (3.20) можно рассчитать толщину поверхностного слоя:

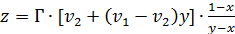(3.23)

При вычислениях по этой формуле предполагают у = х_S. Растворимость и плотность адсорбируемого ПАВ приведены в таблице 4,3.

 

4 Лабораторная работа 1.

Адсорбция поверхностно-активных веществ на

границе раздела жидкость-газ

Цель работы.

Целью данной работы является изучение адсорбции ПАВ на границе

разделаего водного раствора с воздухом.

Приборы и материалы.

Определение поверхностного натяжения осуществлялось двумя методами.

Вариант 1.

Определение поверхностного натяжения методом максимального давления в газовом пузырьке проводится на установке (рисунок 1), состоящей из колбы 1 с пробкой, через которуюпроходит пипеткаскапиллярнымкончиком 2,манометра 3 и водяного эжектора 4, служащего для созданияразрежения в системе.

Объектами исследования служат водные растворы органических кислот испиртов.

Порядок выполнения работы.

С помощью мерной пипетки в колбу 1 заливают 5 мл исходного

Рисунок 4.1 - Схема установки для измерения

поверхностного натяжения.

 

раствораизучаемого ПАВ и закрывают пробкой, в которую вставленапипетка 2 скапиллярным кончиком. Для обеспечения герметичности пробку следует слегка смочить дистиллированной водой. Затем пипетку вращением в пробке перемещают так, чтобы её капиллярный кончик касался поверхностираствора;погружение кончика в раствор недопустимо.

Присоединив колбу 1, проверяют герметичность системы. Для этого закрывают кран 5 и выпускают из эжектора жидкость до тех пор, пока на капиллярном кончике пипетки 2 не начнут выделяться пузырьки воздуха. После этого кран 6 закрывают. Если разность уровней на манометре не уменьшается в течение 1-2 минут, систему можно считать герметичной. В противном случае проверяют плотность соединения резиновых пробок и трубок со стеклом.

Убедившись в герметичности системы, приступают к измерению максимального давления, необходимого для отрыва пузырька газа от кончикапипетки. Для этого открывают нижний кран эжектора и из него по каплям выпускают воду. Скорость вытекания воды должна быть такой, чтобы время образования пузырька было не меньше 10 - 20 сек. При быстром формировании и отрыве пузырька не успевает установиться адсорбционное равновесие на образующейся границе раздела жидкость

– газ и при измерении давления получается заниженный результат. К моменту отрыва пузырька высота Н столба жидкости в одном из колен манометра достигает максимального значения и затем уменьшается. Измеряют и записывают в таблицу 4.1максимальное значение Н. Затем пробку с пипеткой вынимают из колбы иисходный раствор разбавляют, добавляя к нему 1 см³ дистиллированной воды.Колбу закрывают пробкой и раствор аккуратно перемешивают. Промываюткапилляр пипетки новым раствором. Для этого несколько раз набирают впипетку раствор (на высоту 3 –5 мм) с помощьюнадетого на него резинового

 

Таблица 4.1 - Результаты измерений и вычислений.

Объём воды, см3									Н2О
СС, моль/л	1,00	0,830	0,714	0,500	0,333	0,250	0,125	0,067
Н, мм 1 изм. 2 изм. 3 изм.
Нср, мм
σ103, Н/м
Δσ103, Н/м
С/Δσ
Г, кмоль/м2

 

шланга. Затем раствор выдавливают из пипетки.Перед измерением максимального давления в пузырьке в разбавленномрастворе необходимо отрегулироватьположение пипетки в колбе (кончикпипетки должен касаться поверхности раствора) и проверить герметичность системы. Затем по вышеописанной методике измеряют максимальное значение Н, соответствующее отрыву пузырька в разбавленном растворе.

После этого к раствору последовательно добавляют 1,1,3,5,5,20 и 35 см³ дистиллированной воды. Для каждого раствора измеряют Н, предварительно промывая кончик пипетки, регулируя её положение в колбе и проверяя герметичность системы. Результаты измерений заносят в таблицу 4.1.

После измерения Н последнего раствора колбу и пипетку промываютдистиллированной водой и определяют константу К пипетки. Для этого в колбу наливают произвольное количество дистиллированной воды, регулируют положение пипетки, проверяют герметичность и измеряют высоту Н₀ столба манометрической жидкости, соответствующую отрыву пузырькавоздуха в дистиллированной воде. Константу К пипетки рассчитывают по Н₀ и по поверхностному натяжению воды σ_о при температуре опыта:

K= σ_о/H_о.

Значения σ_о приведены в таблице 4.2.

Пользуясь найденной константой,вычисляют поверхностное натяжение всехрастворов σ = KH. (4.1)

Результаты расчетов заносят в таблицу4.1.

 

Таблица 4.2 - Поверхностное натяжение воды при различных

температурах.

t,oC	σ .103, Н/м	t,oC	σ .103, Н/м	t,oC	σ .103, Н/м
	73,49		72,90		71,97
	73,34		72,75		71,82
	73,19		72,59		71,35
	73,05		72,13

 

Оформление результатов работы.

Расчёт удельной адсорбции по уранению Гиббса (3.10) и экспериментально полученной зависимости σ=f(C) проводят в следующей последовательности. Первоначально рассчитывают концентрации С (в кмоль/м³) растворов ПАВ, полученных разбавлением исходного раствора с концентрацией С_о, по формуле:

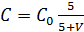(4.2)

Затем проверяется применимость к экспериментальной зависимости σ = f(C) уравнения (3.15). С этой целью при различных концентрациях С рассчитывают С/Δσ и строят график зависимости С/Δσ = f (C). В случае применимости уравнения (3.15) (точки этого графика должны лежать на прямой линии) определяют начальный b ₀ и угловой b ₁ коэффициенты линейной зависимости. Коэффициенты a и b уравнения (3.15) рассчитываются по b ₀ и b ₁ по формулам: , .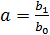

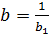По константам a и b и формуле (3.17) вычисляют Г в заданном диапазоне С.

Далее по формулам (3.22) и (3.23) рассчитывают толщину поверхностного слоя растворов ПАВ при различных концентрациях. Плотность и растворимость ПАВ приведены в таблице 4.3.

 

Таблица 4.3 – Плотность и растворимость ПАВ.

Поверхностно-активное вещество	toC	ρ 10-3, кг/м3	xS
Бутиловый спирт		0,810 0,806	0,016 0,019
Изобутиловый спирт		0,803	0,022
Амиловый спирт		0,814	0,0055
Изоамиловый спирт		0,812	0,0059
Гексиловый спирт		0,8136	0,0011
Валериановая кислота		0,939	0,00868
Капроновая кислота		0,929	0,0015

По величине константы b рассчитывают предельную адсорбцию:

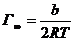(4.3)

Площадь, приходящуюся на одну молекулу ПАВ в насыщенном монослое S₀ итолщину монослоя δ, вычисляют по формулам:

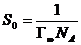и 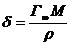. (4.4)

Если при обработке опытных данных будет установлено, что

формула(3.15) не отражает экспериментальную зависимость σ = f (C), то при расчете Г производную dσ/dC следует определять графическим или численным методом.

Применяя графическое дифференцирование, к кривой σ = f(C) строяткасательные в 5 - 7 точках (не обязательно экспериментальных). Для построениякасательной можно воспользоватьсяследующим методом.Вблизи предполагаемой точки касания строят две параллельные хорды(рисунок 4.2а) и через их середины проводят

 

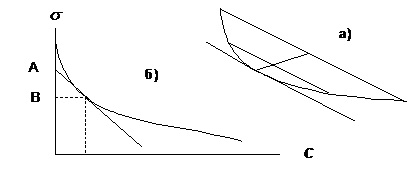
Рисунок 4.2 - Построение касательной к графику функции.

 

прямую до пересечения скривой σ = f(С). Через найденную таким способом точку параллельно хордам проводят касательную до пересечения с осью ординат. Отрезок АВ на оси σ (рисунок 4.2б), деленный на RT, равен удельной адсорбции при концентрации, соответствующей точке касания, т.е. Г =АВ / RT.

Вариант 2.

В данном варианте лабораторной работы поверхностное натяжение

водных растворов органических кислот или спиртов различных концентрацийопределяют сталагмометрическим методом.

На верхний конец сталагмометра (рисунок 2.3) надевают резиновую трубку,используемую для заполнения сталагмометра (с помощью груши) исследуемойжидкостью. Первоначально сталагмометр заполняют дистиллированной водойи определяют количество капель, образующихся из объёма воды, ограниченного на сталагмометре метками. Измерения проводят 3 - 5 раз дополучения воспроизводимого результата. Затем остатки воды удаляют изсталагмометра, его заполняют раствором наименьшейконцентрации и проводят счёт капель,образующихся из этого раствора.Оставшиеся растворы исследуют аналогично в порядке возрастанияконцентрации. Опытные данные заносят втаблицу 4.4.

 

Таблица 4.4- Экспериментальные и расчётные данные.

С, кмоль/м3		0,05	0,1	0,2	0,4	0,6	0,8
n
σ ∙103, Н/м
∆σ ∙103, Н/м
С/∆σ
Г, кмоль/м2

 

Обработку опытных данных проводят по методике, описанной в первомварианте этой работы.