Поверхностное натяжение и капиллярное давление

Важнейшей характеристикой поверхностного слоя является поверхностное натяжение. Оно имеет два определения: механическое и термодинамическое.

Поверхностным натяжением σ называется сила, действующая на единицу длины контура, ограничивающего поверхность, перпендикулярно контуру и по касательной к поверхности. Под действием этой силы площадь поверхности стремится сократиться до минимально возможной величины. При термодинамическом определении под поверхностным натяжением понимают работу, которая совершается при изотермическом и обратимом изменении площади межфазной поверхности на 1 м². Для жидкостей оба определения поверхностного натяжения равнозначны. Как сила поверхностное натяжение имеет размерность «Н/м». Умножая числитель и знаменатель этой дроби на метр, получаем «Дж/м²» - размерность, характерную термодинамическому определению поверхностного натяжения.

В изотропной среде внешнее давление передаётся во всех направленияходинаково (закон Паскаля). Механическое воздействие на поверхностный слой, обладающий анизотропными свойствами, характеризуют не скалярнойвеличиной давления, а тензорной. При механическом воздействии на плоский поверхностный слой различают нормальную Р_N и тангенциальную P_T составляющиедавления.Работаобразованияповерхностногослояплощадью, равной 1м²,определяетсявыражением следующего вида:

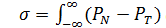, (2.1)

где z - координата, перпендикулярная поверхности раздела.

Поверхностное натяжение жидкостей обусловлено ван-дер-ваальсовым взаимодействием молекул поверхностного слоя. Поэтому оно определяется теми физическими константами, от которых зависит величина ван-дер-ваальсовых сил: дипольным моментом молекул, их поляризуемостью и потенциалом ионизации. Взаимодействие дипольных молекул полярных жидкостей осуществляется за счёт всех трёх составляющих ван-дер-ваальсовых сил (ориентационной, индукционной и дисперсионной), а неполярных – только за счёт дисперсионных сил. Поэтому поверхностное натяжение полярных жидкостей, как правило, больше, чем неполярных.Вода имеет аномально большое поверхностное натяжение, не пропорциональное ее сравнительно небольшому дипольному моменту и небольшой поляризуемости. Эта аномалия воды обусловлена большим влиянием на её свойства специфического вида межмолекулярных сил, называемых водородной связью.

Поверхностное натяжение жидкостей может быть измерено прямыми экспериментальными методами. Ряд методов определения поверхностного натяжения основан на явлениях, связанных с кривизной межфазной границы раздела жидкости и газа.

Если две фазы гетерогенной системы разделены искривлённой границей раздела, то давления в этих фазах различны; в тех же фазах, разделённых плоской границей, они одинаковы. Разность давлений в фазах, разделённых искривлённой границей раздела, называется капиллярным давлением. Капиллярное давление обусловлено действием силы поверхностного натяжения. Например, для выпуклой поверхности жидкости эта сила, действующая по касательной к поверхности, имеет нормальную составляющую σ_N, направленную в объём жидкости, которая и создаёт избыточное (капиллярное) давление в жидкой фазе (рисунок 2.1).

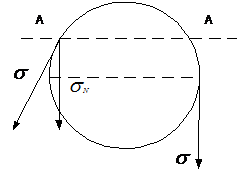
Рисунок 2.1 - Нормальная составляющая силы поверхностного

натяжения, действующая в сечении А-А капли жидкости

и в сечении, проходящем через центр сферы.

Для вогнутой поверхности жидкости центр кривизны расположен в газовой фазе, в которую и направлена нормальная составляющая силы поверхностного натяжения. Поэтому капиллярное давление для вогнутой поверхности считается отрицательным.

Величину капиллярного давления в сферической капле жидкости

можно рассчитать следующим образом. По определению давление представляет собой отношение силы к площади. Поэтому давление, создаваемое силами поверхностного натяжения в сечении, проходящем через центр сферы, будет равно (рисунок 2.1):

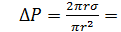(2.2)

Не трудно убедиться в том, что капиллярное давление зависит только от радиуса сферы и не зависит от положения выбранного сечения.

Формула (2.2) является частным случаем следующей формулы, полученной Лапласом,для поверхности произвольной геометрическойформы: 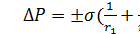, (2.3)

где r₁ и r₂ – главные радиусы кривизны.

У сферической поверхности r₁=r₂=r.

Если давления в газовых фазах над плоской и искривлённой поверхностью жидкости одинаковы (например, равны атмосферному), то капиллярное давление равно разности давлений в жидкости под искривлённой границей раздела Р_r и плоской Р:

Δ Р = Р_r – Р. (2.4)

При таком определении капиллярного давления Р_r>P (∆P>0) для выпуклой поверхности, а для вогнутой Р_r<P (∆P<0).

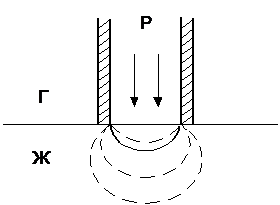
Рисунок 2.2 - Формирование пузырька газа (границы

раздела жидкость-газ) при повышении давления в капилляре.

Один из методов определения поверхностного натяжения основан на манометрическом измерении максимального давления в пузырьке газа, выдуваемого из капилляра в жидкость (рисунок 2.2).

При повышении давления воздуха в капилляре радиус кривизны образующейся вогнутой поверхности жидкость - газ уменьшается; при этомвнешнее давление уравновешивается капиллярным давлением. По достижении давления Р_max, при котором радиус кривизны поверхности равен радиусу капилляра, дальнейшее повышение давления сопровождается увеличением радиуса кривизны и, следовательно, уменьшением капиллярного давления. При Р > Р_max внешнее давление в капилляре становится больше капиллярного давления и пузырёк газа отрывается от конца капилляра. Определив Р_max и зная радиус капилляра, можно по формуле Лапласа рассчитать поверхностное натяжение. На практике коэффициент пропорциональности между Р и σ, зависящий от радиуса капилляра,определяют экспериментально по эталонной жидкости сизвестнымповерхностным натяжением.

Среди методов определения поверхностного натяжения наиболее простым по аппаратурному оформлению является сталагмометрический метод. Прибор для определения σ, называемый сталагмометром,

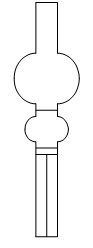
Рисунок 2.3 - Схема сталагмометра.

представляет собой стеклянную трубку с двумя расширениями шаровой формы, заканчивающуюся капилляром (рисунок 2.3). Нижнее расширение сталагмометра ограничено двумя метками.

Сталагмометр заполняется исследуемой жидкостью и закрепляется в вертикальном положении. Под действием силы тяжести на торце капилляра формируется капля жидкости. Она отрывается, когда её весстановится равным силамповерхностного натяжения, противодействующим росту поверхности капли. В первом приближении можно считать, что коэффициент пропорциональности между весом капли и поверхностным натяжением жидкости является константой, характерной применяемому капилляру и независит от природы жидкости. Величину этой константы можно рассчитать, определив вескаплистандартнойжидкости сизвестнымповерхностным натяжением σ_ст.

На практике обычно определяется количество капель n_cm стандартнойжидкости и n -изучаемой, формирующихся из объёма сталагмометра,отмеченного метками. По результатам этих опытов поверхностное натяжение жидкости рассчитывается по следующей формуле: 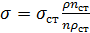_, (2.5)

где ρ и ρ₀ – плотности раствора и стандартной жидкости,

соответственно.

При определении поверхностного натяжения сильно разбавленных растворов можно считать, что плотность растворителя ρ_cm равна плотности растворов ρ. Поэтому 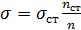. (2.6)