Вступительных испытаний по математике
(для поступающих по программам СПО
На базе 9 класса)
Настоящая Программа составлена в соответствии с Примерной программой основного общего образования по математике
Рассмотрено и одобрено на заседании отборочной комиссии
протокол № 2 от 29 января 2010 года
Общие положения
На экзамене по математике поступающие в техникум должны:
ü знать определения математических понятий, формулировки основных теорем, основные формулы;
ü уметь доказывать теоремы и выводить формулы, проводить доказательные рассуждения в ходе решения задач в устном и письменном изложении;
ü владеть основными умениями и навыками, предусмотренными программой, уметь решать типовые задачи.
Настоящая программа по математике для поступающих в техникум состоит из двух разделов.
В первом разделе перечислены основные математические понятия, которые должен знать поступающий и уметь применять
Второй раздел содержит теоремы и формулы, которые надо уметь формулировать и доказывать. Из вопросов этого раздела формируется содержание теоретической части экзаменационных билетов.
В третьем разделе перечислены основные умения и навыки, которыми должны владеть поступающие.
I. Основные математические понятия и факты
Числа и вычисления
1. Натуральные числа. Делители и кратные натурального числа. Четные и нечетные числа. Признаки делимости на 2, 3, 5, 10 и 9. Простые составные числа. Понятие о разложении натурального числа на простые множители. Наибольший общий делитель. Наименьшее общее кратное.
2. Положительные и отрицательные числа. Противоположные числа. Модуль числа, его геометрический смысл. Сравнение положительных и отрицательных чисел.
3. Обыкновенная дробь. Сравнение обыкновенных дробей. Правильные и неправильные дроби. Целая и дробная часть числа. Основное свойство дроби. Среднее арифметическое нескольких чисел.
4. Десятичная дробь. Приближенное значение числа. Округление чисел. Проценты. Основные задачи на проценты.
5. Понятие очисле как результате измерения. Рациональные числа. Представление рациональных чисел в виде периодических бесконечных десятичных дробей.
6. Изображение чисел на прямой. Координата точки. Прямоугольная система координат на плоскости, абсцисса и ордината точки.
7. Пропорция. Основное свойство пропорции. Понятие о прямой и обратной пропорциональности величин.
8. Понятие об иррациональных числах. Действительные числа. Числовые неравенства и их свойства. Почленное сложение и умножение числовых неравенств.
9. Понятие об изменении величин, абсолютной и относительной погрешности приближенного значения. Запись чисел в стандартном виде.
10. Квадратный корень и кубический корень.
Выражения и их преобразования
1. Числовые выражения. Применение букв для записи выражений.
Числовое значение буквенного выражения. Вычисления по формулам.
Простейшие преобразования выражений: раскрытие скобок, приведение
подобных слагаемых.
2. Многочлен. Степень многочлена. Сложение, вычитание, умножение многочленов. Разложение многочлена на множители. Формулы сокращенного умножения.
3. Квадратный трехчлен. Разложение квадратного трехчлена на множители.
4. Алгебраическая дробь. Основное свойство дроби. Сокращение алгебраических дробей. Сложение, вычитание, умножение и деление алгебраических дробей.
5. Степень с натуральным показателем и ее свойства. Степень с целым показателем. Свойства квадратных корней. Преобразования выражений, содержащих квадратные корни.
6. Корень n -й степени и его свойства. Степень с рациональным показателем и ее свойства.
7. Основные тригонометрические тождества sin2x + cos2x = 1; tgx = sinx/cosx.
8. Формулы приведения (без доказательства). Синус и косинус суммы и разности двух углов, синус и косинус двойного угла. Тождественные преобразования тригонометрических выражений.
9. Арифметическая прогрессия. Формулы n -го члена и суммы n первых членов арифметической прогрессии.
10. Геометрическая прогрессия. Формулы n -го члена и суммы n первых ее членов.
Уравнения и неравенства
1. Уравнение. Корни уравнения. Линейные уравнения с одним неизвестным. Квадратное уравнение; формулы корней. Рациональное уравнение и его решение.
2. Система уравнений. Решение системы двух линейных уравнений с двумя неизвестными и его геометрическая интерпретация. Решение простейших систем, содержащих уравнение второй степени.
3. Линейное неравенство с одним неизвестным. Система линейных неравенств с одним неизвестным. Решение рациональных неравенств методом интервалов. Решение неравенств второй степени с одним неизвестным.
Функция
1. Функция. Область определения функции, область значения. Способы задания функции. График функции. Возрастание и убывание функций, сохранение знака.
2. Функции: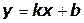 
; 
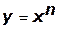(n — натуральное число);
, 
, 
, 
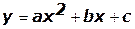. Их свойства и графики.