Построение проекций точки и прямой, принадлежащих заданной плоскости, выполняется на основании известных аксиом:
1. Через две любые различные точки можно провести только одну прямую.
2. Если две точки прямой принадлежат плоскости, то и все точки этой прямой принадлежат заданной плоскости.
Решение этих задач основывается на известных положениях геометрии:
1. Точка принадлежит плоскости, если она принадлежит прямой этой плоскости.
2. Прямая принадлежит плоскости, если она проходит через две точки, принадлежащие плоскости, или через одну точку этой плоскости параллельно прямой, лежащей в этой плоскости или ей параллельной.
По свойству принадлежности точки прямой – ее проекции лежат на одноименных проекциях прямой, принадлежащей плоскости.
Построение любой прямой в плоскости
Для этого достаточно (рис. 58 а) на проекциях плоскости взять проекции двух произвольных точек, например: m', m и n', n, и через них провести проекции m'n', mn прямой MN. На рис. 58 б проекции b'n', bn прямой ВN проведены параллельно проекциям а'с', aс стороны АС треугольника, заданного проекциями а'b'с', abc. Прямая ВN принадлежит плоскости треугольника ABC.
|
|
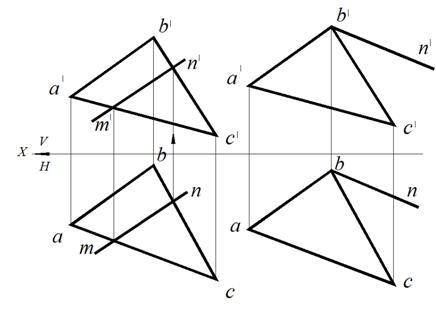
Рис. 58. Построение прямой в плоскости:
а – через две произвольные точки М и N; б – параллельно прямой АС
Построение недостающей проекции точки, принадлежащей заданной плоскости
Задача. Построить в плоскости, заданной треугольником DЕС, недостающие проекции точки А и точки В,принадлежащих плоскости заданного треугольника (рис. 59).
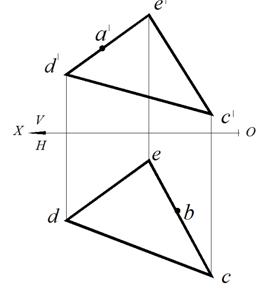
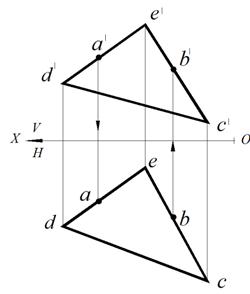
Рис. 59. Условие задачи Рис. 60. Построение в плоскости точки
Решение
Анализируя графическое условие задачи, видим, что точка А принадлежит прямой DЕ. Следовательно, по свойству принадлежности, ее горизонтальная проекция тоже принадлежит горизонтальной проекции прямой DE. Проводим линию связи из фронтальной проекции точки А до пересечения с горизонтальной проекцией прямой DЕ. Полученная точка будет горизонтальной проекцией точки А. Аналогично строим фронтальную проекцию точки В (рис. 60).
Задача. Построить фронтальную проекцию точки Е, лежащей в плоскости, заданной двумя параллельными прямыми AB и CD.
Решение
На рис. 61 плоскость задана проекциями a'b' || c'd', ab || cd. Принадлежащая этой плоскости точка E задана горизонтальной проекцией e. Следует достроить фронтальную проекцию точки Е. Ее строят с помощью вспомогательной прямой, принадлежащей плоскости и проходящей через точку D. Такое действие называется привязкой точки к плоскости. Для этого проводят через горизонтальную проекцию d и е прямую. Отмечают точку пересечения этой прямой с прямой ab – точку n. Строят фронтальную проекцию прямой n'd' и по линии связи отмечают на ней фронтальную проекцию точки Е – е' (рис. 62).
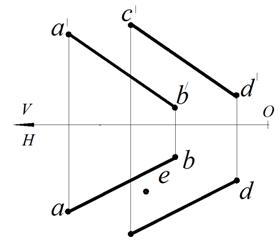
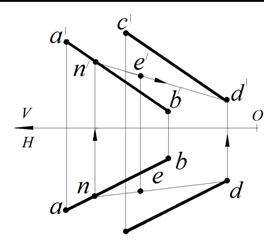
Рис. 61. Условие задачи Рис. 62. Построение недостающей
проекции точки
Проверка принадлежности точки плоскости
Задача. Определить принадлежность точки А плоскости, заданной треугольником DFE
(рис. 63).
Решение
Для проверки принадлежности точки плоскости используют вспомогательную прямую, принадлежащую плоскости. Предполагают, что заданная точка принадлежит заданной плоскости. Следовательно, она принадлежит любой прямой, лежащей в заданной плоскости. Поэтому точку А «привязываем» к плоскости треугольника прямой. Для этого на горизонтальной проекции проводим прямую через точку а и точку b. Отмечаем точку пересечения проведенной прямой со стороной dc – точку b. Строим фронтальную проекцию полученной прямой b'e'. Анализируя чертеж, видим, что фронтальная проекции точки А не принадлежит прямой ВЕ. Следовательно, заданная точка А не принадлежит заданной плоскости треугольника DEC. (рис. 64).
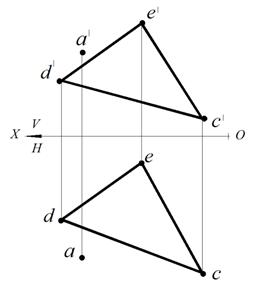
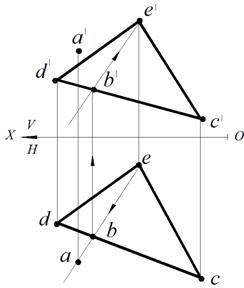
Рис. 63. Условие задачи Рис. 64. Проверка принадлежности
точки плоскости