Цель: формирование умения классифицировать функции, исследовать функции, заданные графически, строить графики функций методом преобразований, решать уравнения и неравенства графическим способом, решать прикладные задачи, содержащие функциональные зависимости.
& 35.1.Разберите:
· какие существуют виды функций и как проходят их графики;
· какова техника решения уравнений и неравенств графическим способом;
· какие преобразования графиков функции возможны.
Основные сведения из теории:
35.2. Закончите определение:
Функция - …
| Функция называется | степенной | если она задаётся уравнением | … |
| показательной | … | ||
| логарифмической | … | ||
| тригонометрической | … |
Примеры и упражнения:
?35.3. Установите соответствие:
| График функции | Аналитическое задание функции |
А.  Б. Б.  В.
В.  Г. Г.  Д. Д.  Е.
Е. 
| 1.  2.
2.  3.
3.  4.
4.  5.
5.  6.
6.  7.
7.  8.
8.  9.
9.  10.
10. 
|
 ?35.4. Функция заданна графически. Пользуясь графиком, найдите:
?35.4. Функция заданна графически. Пользуясь графиком, найдите:
а) период функции,
б) нули функции на отрезке  ;
;
в) промежутки убывания функции;
г) промежутки, на которых функция принимает положительные значения.
?35.5. Решите графически уравнение:  .
.
?35.6. (ЕГЭ) Деталью некоторого прибора является квадратная рамка с намотанным на неё проводом, через который пропущен постоянный ток. Рамка помещена в однородное магнитное поле так, что она может вращаться. Момент силы Ампера, стремящейся повернуть рамку, (в Н  м) определяется формулой
м) определяется формулой  , где
, где  – сила тока в рамке,
– сила тока в рамке, 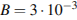 Тл – значение индукции магнитного поля,
Тл – значение индукции магнитного поля,  м – размер рамки,
м – размер рамки, 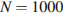 – число витков провода в рамке,
– число витков провода в рамке,  – острый угол между перпендикуляром к рамке и вектором индукции. При каком значении угла
– острый угол между перпендикуляром к рамке и вектором индукции. При каком значении угла  (в градусах) рамка начнёт вращаться, если для этого нужно, чтобы раскручивающий момент M был 0,75 Н
(в градусах) рамка начнёт вращаться, если для этого нужно, чтобы раскручивающий момент M был 0,75 Н  м?
м?
?35.7. Постройте график функции методом преобразований:
а)  ; б)
; б)  .
.
¶35.8. Решите графически систему уравнений: 
Список литературы:
1. Богомолов Н.В. Математика: учеб. для ссузов / Н.В. Богомолов, П.И. Самойленко. – М.: Дрофа, 2015.- 395 с. - Глава 2, §14 - 17, стр. 103 – 118, глава 3, §37, стр. 171 – 177.
Раздел 1. АЛГЕБРА И НАЧАЛА АНАЛИЗА
Тема 1.5. Уравнения и неравенства
Задание 36. Основные приёмы решения систем уравнений – 1 ч.
Цель: формирование умения решать уравнения и их системы.
Задание для самостоятельной внеаудиторной работы:
& 36.1.Повторите определение уравнения, понятие равносильности уравнений. Вспомните основные виды уравнений и методы их решения. Разберите основные методы решения систем уравнений.
Основные сведения из теории:
36.2. Закончите определение:
Уравнение - …
Два уравнения называются равносильными, если …
Основными методами решения систем уравнений являются …
В методе подстановки необходимо …
Метод алгебраического сложения предполагает …
Примеры и упражнения:
?36.3. Решите систему уравнений методом подстановки:
а)  ; б)
; б) 
?36.4. Решите систему уравнений методом алгебраического сложения:
а)  ; ¶б)
; ¶б) 
?36.5. Применяя графический метод, определите, сколько решений имеет система уравнений:

Список литературы:
1. Богомолов Н.В. Математика: учеб. для ссузов / Н.В. Богомолов, П.И. Самойленко. – М.: Дрофа, 2015.-395 с. - Глава 1, §7, 12, стр. 57, 98.
Раздел 1. АЛГЕБРА И НАЧАЛА АНАЛИЗА
Тема 1.5. Уравнения и неравенства