измерений
Метрологическая характеристика (MX) средства измерения —
это характеристика одного из свойств СИ, влияющая на результат
измерений и на его погрешность. Для каждого типа СИ устанавли-
ваются свои MX. Метрологические характеристики, устанавливаемые
в нормативно-технической документации (НТД) на данное СИ, на-
зываются нормируемыми MX, а определяемые экспериментально —
действительными MX.
К метрологическим характеристикам относятся статические и
динамические характеристики, чувствительность, порог чувствитель-
ности, диапазон измерения, цена деления шкалы и т. д. Статическая
характеристика (СХ) — это функциональная зависимость выходной
величины у от входной х в статическом режиме (рис. 1.2). При этом
режиме входные и выходные величины СИ не изменяются во време-
ни (стационарный или равновесный режим). Более точно СХ можно
определить как зависимость информативного параметра выходного
сигнала от информативного параметра входного сигнала в статиче-
ском режиме. В общем случае эта зависимость представляет собой
некоторое нелинейное уравнение преобразования у = f(x). Для из-
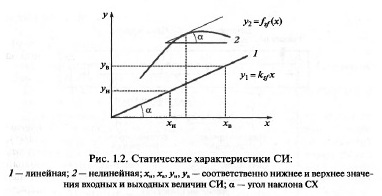
мерительных преобразователей и измерительных приборов с неиме-
нованной шкалой или со шкалой, отградуированной в единицах,
отличных от единиц измеряемой величины, СХ называется также
функцией преобразования, а для остальных измерительных прибо-
ров — характеристикой шкалы.
В реальных условиях эксплуатации на СИ действуют влияющие
факторы ср (внутренние и внешние), которые не несут информацию
об измеряемом параметре. Если они не равны нормам, то зависимость
у = f(x) называется рабочей СХ, а если равны — номинальной или
градуировочной СХ у = fу(x). Градуировочные характеристики СИ
получаются экспериментальным путем и могут быть заданы в виде
формул, графика или таблицы (например, градуировочные таблицы
для термометров сопротивления и термопар).
Важным параметром СИ является угол наклона статической ха-
рактеристики к оси абсцисс (для линейных СХ) или касательной к
этой характеристике в точке отсчета (для нелинейных СХ). Тангенс
угла наклона называется чувствительностью СИ (5). Чувствитель-
ность СИ — это свойство, определяемое отношением изменения
выходного сигнала этого средства к вызывающему его изменению
измеряемой величины:

Различают абсолютную и относительную чувствительности.
Абсолютная чувствительность определяется по формуле

а относительная — по формуле
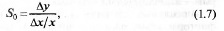
где ∆у — изменение сигнала на выходе СИ; ∆х — изменение изме-
ряемой величины; х — измеряемая величина.
Если статическая характеристика СИ нелинейна, то чувствитель-
ность в различных точках диапазона будет различной, а шкала — не-
равномерной. При линейной статической характеристике чувстви-
тельность СИ постоянна, а шкала равномерная.
Порог чувствительности СИ — это наименьшее значение из-
менения ФВ, начиная с которого может осуществляться ее измерение
данным средством.
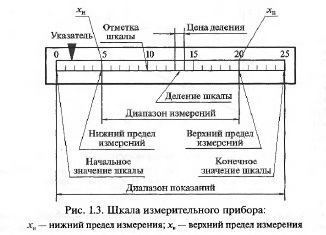
Для шкальных отсчетных устройств используются характеристики,
показанные на рис. 1.3.
Цена деления шкалы (постоянная прибора) — разность значений
величины, соответствующих двум соседним отметкам шкалы СИ, т. е.
количество единиц величины, содержащихся в одном делении шкалы.
Диапазон измерений — область значений величины, в пределах ко-
торой нормированы допускаемые пределы погрешности СИ. Значе-
ния величины, ограничивающие диапазон измерений снизу и сверху
(слева и справа), называют соответственно нижним хн и верхним хв
пределом измерений. Область значений шкалы, ограниченная на-
чальным и конечным значениями шкалы, называется диапазоном
показаний.
Цена деления шкалы С однозначно связана с числом делений п
шкалы и чувствительностью S:

а число делений п — с классом точности (А) СИ: п > 10/2А (понятие
класса точности будет дано в подразд. 1.6).
Поэтому значение измеряемой величины должно быть отсчитано
по шкале с погрешностью в половину деления.
Динамическая характеристика СИ (рис. 1.4) — это зависимость
выходного сигнала от входного в динамическом режиме (в этом
режиме входные и выходные величины изменяются во времени)
y(t) = ƒ[х[(t) ] ]. Динамический (неустановившийся, или переходный)
режим — переход СИ из одного установившегося режима в другой.
Так как практически все СИ имеют в своем составе инерционные
элементы (подвижные механические узлы; электрические, пневмати-
ческие или гидравлические емкости, индуктивности; элементы, об-
ладающие тепловой инерцией, и т.д.), то при мгновенном изменении
входного сигнала выходной сигнал изменяется с запаздыванием по
определенному закону (кривые переходных процессов, или кривые
разгона). Закон изменения этих характеристик может быть колебатель-
ным, апериодическим, дифференциальным, интегральным. Динами-
ческие характеристики описываются дифференциальными уравне-
ниями, передаточной функцией, амплитудно-фазовой, амплитудно-
частотной и фазо-частотной характеристиками (см. гл. 13), а также
переходной и импульсной функциями. Для определения параметров
динамических характеристик СИ используют теорию автоматическо-
го управления (регулирования). Важным параметром динамического
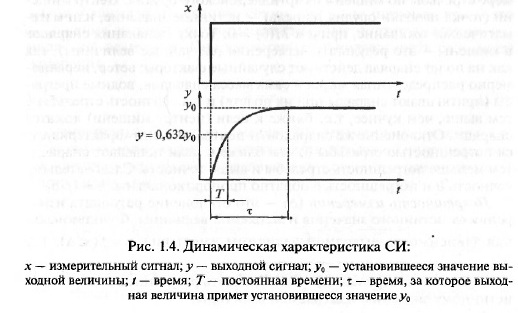
режима является время завершения переходного процесса (проме-
жуток времени т от момента подачи измерительного сигнала х до
момента установления постоянного выходного сигнала у = const). На
практике широко используется постоянная времени Т(это время, за
которое выходной сигнал достиг бы нового установившегося значе-
ния, если бы изменялся с постоянной скоростью, равной начальному
значению). Обычно за Т принимают время, за которое выходная
величина у достигает уровня у = 0,632у0, где у0 — установившееся
значение выходной величины.
1.6. Погрешности измерений и средств
измерений
При любых измерениях важно оценить их точность. Термин «точ-
ность измерения», т.е. степень приближения результатов к некото-
рому истинному значению, не имеет строгого определения и исполь-
зуется для качественного сравнения измерительных операций. Для
количественной оценки существует понятие «погрешность измере-
ния». Любой результат измерения является случайным, поэтому для
оценки его достоверности используются две характеристики: мате-
матическое ожидание М (0) = х — среднее значение, вокруг кото-
рого группируются все случайные результаты измерения х,...х„, и
дисперсия D( Ɵ) — степень разбросанности результатов относитель-
ного математического ожидания.
Понятия «точность» и «погрешность» можно пояснить на при-
мере стрельбы по мишени из артиллерийского орудия. Центр мише-
ни (точка наводки орудия на цель) — истинное значение, или мате-
матическое ожидание, причем M(Q) = 0. Точки попадания снарядов
в мишень — это результаты измерения (случайные величины), так
как на полет снаряда действуют случайные факторы: ветер, неравно-
мерно распределенная масса и сама масса снарядов, водные прегра-
ды (притягивают снаряды при их полете) и т.д. Точность стрельбы h
тем выше, чем кучнее, т.е. ближе к цели (центру мишени) ложатся
снаряды. Отклонение же снарядов от центра мишени характеризует-
ся погрешностью стрельбы δ; чем ближе к цели попадают снаряды,
тем меньше погрешность стрельбы и выше точность. Следовательно,
точность h и погрешность δ обратно пропорциональны: h- 1/|δ|.
Погрешность измерения (∆) — это отклонение результата изме-
рения от истинного значения измеряемой величины. Функциональ-
ная зависимость выходной величины имеет вид х = ƒ(х; δ), где
∆ = х-х — погрешность результата.
Точность измерения (h) — это близость результатов измерения к
истинному значению измеряемой вели чины.
В общем виде погрешность измерения имеет следующие состав-
ляющие:
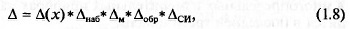
где ∆(х) — погрешность от нестабильности измеряемой величины х;
∆наб — погрешность наблюдателя; ∆м — погрешность метода измере-
ния; ∆обр — погрешность метода обработки результата; ∆сИ — погреш-
ность применяемого средства измерения.
Символом «*» обозначены знаки неопределенности суммирования
между составляющими погрешности измерения, так как вопрос о
законах сложения решается в каждом конкретном случае.
Таким образом, понятия погрешность измерения и погрешность
СИ отличаются друг от друга. Первые четыре составляющие погреш-
ности измерения могут быть уменьшены или даже сведены к нулю.
Последняя погрешность ∆си — погрешность СИ — является неустра-
нимой погрешностью.
Погрешности средств измерения ∆си классифицируются по ряду
признаков.
По форме з а п и с и погрешности СИ делятся на абсолютную ∆,
относительную δ и приведенную γ. Абсолютная погрешность — это
разность между результатом и истинным значением измеряемой ве-
личины:
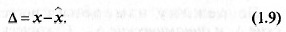
Эта погрешность характеризует только количественную сторону
результата измерения, но не отражает качественную сторону про-
цесса измерения; например, погрешность измерения расстояния
между двумя объектами ∆ = 2 км не позволяет однозначно сделать
вывод о качестве измерения. Относительная погрешность — это
отношение абсолютной погрешности к истинному значению из-
меряемой величины. Она характеризует погрешность результата
измерения
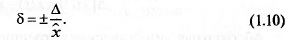
Измерительный прибор измеряет ФВ переменного значения. Его
качество не может характеризоваться относительной погрешностью,
так как она уменьшается с увеличением истинного значения изме-
ряемой величины:
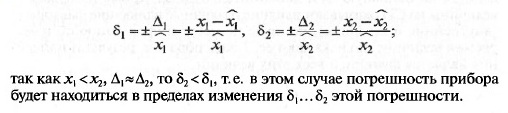
Любое же СИ должно характеризоваться одной погрешностью.
Исходя из этого существует «золотое правило» в метрологии:
в многопредельных измерительных приборах измерение ФВ прово-
дится в последней трети шкалы.
Качество измерительного прибора характеризуется приведенной
погрешностью. Приведенная погрешность — это отношение абсо-
лютной погрешности к базовому значению:

где N = const — базовое значение, за которое в измерительных при-
борах принят диапазон измерения N = (хв-хн).
На практике вместо истинного значения измеряемой величины
используется ее действительное значение:

Относительная и приведенная погрешности могут выражаться не
только в безразмерных единицах, но и в процентах:
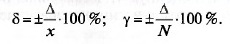
По режиму и з м е р е н и я погрешности делятся на статиче-
ские ∆s, и динамические ∆dy. Статическая погрешность формируется
в статическом режиме. Абсолютная погрешность СИ в статическом
режиме
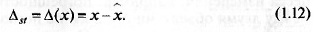
В динамическом режиме формируется динамическая погрешность.
Абсолютная погрешность СИ в динамическом режиме

По в н е ш н и м у с л о в и я м п р и м е н е н и я СИ погрешности
делятся на основную ∆0 и дополнительную ∆с. Кроме измеряемой
величины на СИ оказывают влияние различные влияющие факторы φ,
(внутренние и внешние), которые не несут информацию об изме-
ряемой величине, но искажают ее. Таким образом, результат измере-
ния является функцией всех этих величин:
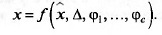
Для каждого СИ в нормативно-технической документации (НТД)
указываются диапазоны изменения влияющих факторов, которые для
данного СИ являются нормами (φref). Эти значения могут быть даны
в виде одного числа (влажность Wref = 60%) или в виде диапазона
чисел (Ɵге/ = (20 ± 5) °С, Uref = 220 ±j° В)• Если в условиях эксплуатации
СИ влияющие факторы имеют нормальные значения или находятся
в пределах нормальной области этих значений (φ, = φге/), то такие
условия эксплуатации называются нормальными, а погрешность СИ,
формируемая в этих условиях, — основной, так как присуща только
самому СИ, отражает свойство только самого СИ и является его
основной (главной) погрешностью. Результат, полученный в нормаль-
ных условиях эксплуатации, равен

и формируется по каждому влияющему фактору φi.
Суммарная дополнительная погрешность ∆с равна
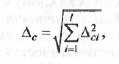
где ∆ci — дополнительная погрешность по φ, влияющему фактору;
l — число влияющих факторов.
В НТД на СИ кроме нормальных указываются также рабочие об-
ласти влияющих величин φi и дополнительные погрешности по
каждой из них, что позволяет определить общую погрешность для
конкретных условий измерения (если они не выходят за пределы
рабочих условий эксплуатации).
По х а р а к т е р у п о я в л е н и я погрешности СИ делятся на
систематическую ∆s и случайную ∆. Систематической называют
составляющую погрешности, остающуюся постоянной или изменяю-
щуюся по определенному закону от измерения к измерению. Обыч-
но систематические погрешности исключаются из результата изме-
рения различными способами. Случайной называют составляющую
погрешности, которая изменяется случайным образом при повторных
измерениях одного и того же истинного значения измеряемой вели-
чины. Исключить ее из результата невозможно, но оценить необхо-
димо. Для этого используются теория вероятностей и математическая
статистика.
По з а в и с и м о с т и между в е л и ч и н о й п о г р е ш н о с ти
и з н а ч е н и е м и з м е р я е м о й в е л и ч и н ы погрешности СИ
делятся на аддитивные, мультипликативные и гистерезиса.
Аддитивная погрешность постоянна по величине и не зависит от
значения измеряемой величины: ∆а(хi) = +а. Ее причиной, напри-
мер, может быть сбитая шкала СИ.
Мультипликативная погрешность пропорциональна измеряемой
величине: ∆ м (хi) = ± bx; ее причиной может быть, например, изме-
нение параметров отдельных элементов.
Погрешность гистерезиса — это несовпадение результатов из-
мерений при прямом и обратном ходе (причинами гистерезиса явля-
ются люфт, сухое трение, упругое последействие и т. п.). Количествен-
но погрешность гистерезиса (вариация) определяется как разность
между результатами измерений одного и того же значения измеряемой
величины, полученными при движении со стороны меньших значе-
ний до данного значения (прямой ход) и со стороны больших значе-
ний до данного значения (обратный ход). Вариация Н для стрелочных
приборов определяется по формуле Н = |х'-х"|,
где х' и х" — результаты, полученные соответственно при прямом и
обратном ходе.
При технических измерениях каждому СИ присваивается опреде-
ленный класс точности. Класс точности (А) — это обобщенная
метрологическая характеристика, определяющая различные свойства
СИ и включающая в себя систематическую и случайную составляю-
щий погрешности. Класс точности нормируется предельными значе-
ниями основной погрешности в виде абсолютной, относительной или
приведенной.
Классами точности, определенными по абсолютной погрешности
∆ор, нормируются меры. Такой класс точности обозначается римской
цифрой или прописной буквой латинского алфавита, причем чем
больше цифра или дальше буква от начала алфавита, тем больше по-
грешность.
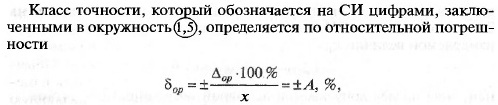
где х — результат измерения. Такими классами точности нормируют-
ся мосты переменного тока, счетчики электрической энергии, дели-
тели напряжения, измерительные трансформаторы. Цифровые СИ
нормируются классами точности, которые также определяются от-
носительной погрешностью
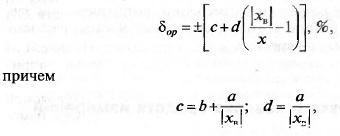
где а = ∆а(х) и b = ∆м(х) — аддитивная и мультипликативная состав-
ляющие погрешности соответственно; хi — верхний предел измерения
СИ. Такой класс точности может быть обозначен, например, 0,02 /0,01
(с = 0,02, d = 0,01). При нормировании класса точности по приве-
денной погрешности γор для СИ с неравномерной шкалой (например,
омметров и амперметров) она определяется по формуле
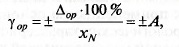
где xN — длина шкалы или ее части; обозначается такой класс точ-
ности на СИ цифрами с галочкой внизу — 1^5.
Для нормирования класса точности всех аналоговых СИ исполь-
зуется приведенная погрешность
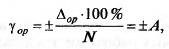
где N= хв-хи — предел измерения СИ.
Обозначается такой класс точности цифрами, например: 2,0. От-
влеченные положительные числа А, с, d в формулах выбираются из
ряда (1,0; 1,5; 2,0; 2,5; 4,0; 5,0; 6,0)10", где п = -3; -2; -1; 0; 1, и назы-
ваются классами точности.
Средство измерений может иметь два и более классов точности.
Например, при наличии у него двух и более диапазонов измерений
одной и той же физической величины (многопредельные измеритель-
ные приборы) или при измерении одним СИ нескольких физических
величин (разные классы точности для каждой измеряемой величины).
Зная класс точности СИ, можно определить действительное значение
измеряемой величин хд:
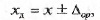
или, зная предел допускаемой основной погрешности ∆ор, соответ-
ствует ли данное СИ своему классу точности.
Показателями качества измерения являются также правильность,
сходимость и воспроизводимость измерений. Правильность отража-
ет близость к нулю систематических погрешностей в их результатах.
Сходимость отражает близость друг к другу результатов измерений,
выполняемых в одинаковых условиях. Воспроизводимость отражает
близость друг к другу результатов измерений, выполняемых в раз-
личных условиях (в разное время, в различных местах, разными
методами и средствами измерения).
1.7. Градуировка и поверка средств измерений
Все СИ перед эксплуатацией подлежат процедуре градуировки,
а в процессе эксплуатации — периодической процедуре поверки.
Градуировка — это операция нанесения на шкалу СИ отметок, соот-
ветствующих показаниям рабочего эталона (для измерительных
приборов), или определения градуировочной характеристики СИ (для
измерительных преобразователей). Поверка — это операция, прово-
димая метрологическими службами и заключающаяся в установлении
пригодности СИ к применению на основании экспериментально
определенных метрологических характеристик и контроля их соот-
ветствия НТД. Основной метрологической характеристикой, опреде-
ляемой при поверке СИ, является его погрешность. Она находится
на основании сравнения поверяемого СИ с более точным рабочим
эталоном.
Поверка измерительных приборов проводится одним из двух ме-
тодов:
1) непосредственное сравнение величин, измеряемых СИ, и ве-
личин, воспроизводимых рабочими эталонами соответствующего
класса точности;
2) непосредственное сличение показаний поверяемого и некото-
рого рабочего эталона при измерении одной и той же величины.
Основой данного метода служит одновременное измерение одного и
того же значения физической величины поверяемым СИ и рабочим
эталоном. Разность показаний этих приборов равна абсолютной по-
грешности поверяемого СИ.
Важным при поверке является выбор оптимального соотношения
между допускаемыми погрешностями рабочего эталона и поверяе-
мого СИ. Обычно рабочие эталоны выбираются таким образом,
чтобы это соотношение было 1:5.
Контрольные вопросы
1. Что означает понятие «метрология»?
2. В чем разница между истинным и действительным значением физиче-
ской величины?
3. Что такое шкала отношений? Приведите пример такой шкалы.
4. Что такое дольные и кратные единицы измерений?
5. Какие измерения относятся к косвенным? Приведите пример.
6. Какие причины могут привести к появлению аддитивной погрешно-
сти?
7. В чем заключается разница между погрешностью измерения и погрешно-
стью средства измерения?
8. Приведите классификацию средств измерения.
9. Что понимается под нормальными условиями измерения?
10. Может ли средство измерения иметь несколько классов точности?
11. В чем состоит разница между поверкой и градуировкой?
Гл а в а 2
ЭЛЕКТРИЧЕСКИЕ ДАТЧИКИ МЕХАНИЧЕСКИХ ВЕЛИЧИН
2.1. Индуктивные датчики
Принцип работы индуктивных датчиков (ИД) основан на изме-
нении индуктивности или взаимоиндуктивности обмотки с магни-
топроводом вследствие изменения магнитного сопротивления маг-
нитной цепи датчика под воздействием измеряемой величины. ИД
относятся к классу параметрических датчиков. Наиболее широко ИД
применяются для преобразования линейных и угловых перемещений,
а также технологических параметров, преобразуемых в перемещение
(давление, расход и др.). Они также используются в дефектоскопии
для определения наличия дефектов, толщины немагнитных покрытий
на стали и в ряде других областей.
Простейший одинарный (однотактный) ИД линейного пере-
мещения (рис. 2.1, а) с переменным воздушным зазором 5, значение
которого является измеряемой величиной, состоит из сердечника 1,
подвижного якоря 2, связанного с контролируемым объектом X, и
обмотки питания 3, которая является одновременно измерительной
обмоткой. В этом датчике происходит цепочка преобразований
Х-» δ-» Rm -» L, где X— измеряемое перемещение; δ —
воздушный зазор между сердечником и якорем; RM — магнитное
сопротивление цепи датчика; Ф — магнитный поток; L — индуктив-
ность обмотки 3; Z— ее полное сопротивление; I — ток в обмотке.
Статическая характеристика датчика представляет собой зависи-
мость тока в обмотке от зазора δ. Ток I в обмотке

где Uп — напряжение питания; R — активное сопротивление обмот-
ки; ω — циклическая частота напряжения питания; L — индуктив-
ность обмотки.
Поскольку R << ω, активным сопротивлением можно пренебречь.
Индуктивность L и магнитный поток Ф равны соответственно
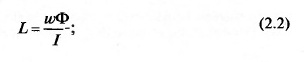

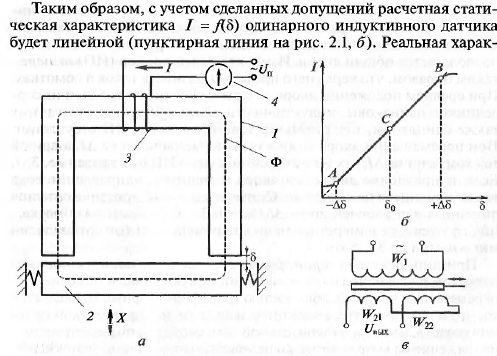

теристика (сплошная линия на том же рисунке) на начальном (до
точки А) и конечном (после точки В) участках отличается от рас-
четной. Это связано с тем, что при малом зазоре RM становится
сопоставимым с Rme, а при большом зазоре начинает влиять актив-
ное сопротивление R обмотки. Участок АВ является рабочей зоной
датчика. По ее центру выбирается начальное значение зазора δ0
(точка С).
Одинарные ИД имеют небольшое относительное перемещение
∆δ/δ0 = 0,1...0,15. Целый ряд недостатков, таких как малая рабочая
зона, невысокая чувствительность, влияние на результат преоб-
разования электромагнитного усилия притяжения якоря к сердеч-
нику, колебания температуры и напряжения питания, существенно
ограничивает их практическое использование. Обычно такие дат-
чики применяются в тех случаях, когда необходимо ступенчатое
релейное управление, например в качестве бесконтактных датчиков
положения, концевых выключателей, датчиков положения и др. Для
измерения же небольших перемещений применяются двухтактные
(реверсивные) ИД, включаемые по дифференциальной схеме. Эти
датчики состоят из двух сердечников, идентичных по конструктив-
ным и магнитным параметрам, с двумя также одинаковыми обмот-
ками, включенными последовательно и встречно. Между ними
располагается общий якорь. Измерительный прибор (ИП) включен
таким образом, что через него протекает разность токов в обмотках.
При среднем положении якоря зазоры между ним и каждым из сер-
дечников одинаковы, индуктивности обеих обмоток и токи в них
также одинаковы, т.е. результирующий ток через ИП отсутствует.
При перемещении якоря один из токов уменьшится на А/, а другой
ток возрастет на ∆I, в результате чего ток через ИП будет равен I = 2∆I.
Если направление движения якоря изменится, направление тока
также изменится на обратное. Статическая характеристика остается
линейной для рабочей зоны ∆δ/δ0 = 0,3...0,4. Такие датчики ис-
пользуются для измерения малых перемещений (от сотых долей
микрометра до 3... 5 мм).
Принцип действия трансформаторных (взаимоиндуктивных)
датчиков также основан на изменении индуктивности обмоток при
перемещении якоря. Особенностью трансформаторных ИД является
то, что в них отсутствует электрическая связь между обмоткой пита-
ния (возбуждения) и измерительной обмоткой, что позволяет менять
напряжение на выходе нагрузки независимо от величины напряжения
источника питания. Наводимая в измерительной обмотке ЭДС
Е равна

где Wи — число витков измерительной обмотки; ω — циклическая
частота напряжения питания; Ф — амплитуда магнитного потока; δ —
воздушный зазор между якорем и сердечником.
Следовательно, изменяя Wи, можно получить любое требуемое
значение выходного сигнала. Наибольшее распространение получил
дифференциально-трансформаторный датчик (рис. 2.1, в), принцип
действия которого основан на изменении потокосцепления между
двумя системами обмоток при перемещении подвижного плунжера.
Первичная обмотка W1 равномерно распределена по длине датчика.
Две одинаковые вторичные обмотки W21 и W22, расположенные на
разных половинах датчика, включены последовательно и встречно.
При симметричном расположении подвижного плунжера ЭДС Ег1 и
Е22 наводимые во вторичных обмотках, компенсируют друг друга,
поэтому UВЫХ = 0. При перемещении плунжера появится выходное
напряжение UВЫХ = Е21 - Е22, фаза которого будет зависеть от направ-
ления перемещения плунжера.
Существуют также трансформаторные датчики угла поворота.
Индуктивные датчики обладают такими достоинствами, как
простота конструкции и надежность в работе; большая выходная
мощность, позволяющая во многих случаях обойтись без усилителя;
высокая чувствительность и разрешающая способность; безынерци-
онность (при условии, что частота изменения измеряемого переме-
щения гораздо меньше частоты источника питания); наличие на
статической характеристике большого линейного участка; возмож-
ность работы непосредственно от сети переменного тока.
2.2. Емкостные датчики
Принцип действия емкостных датчиков (ЕД), которые также
являются датчиками параметрического типа, основан на изменении
емкости конденсатора под воздействием измеряемой величины. Чаще
всего ЕД выполняются в виде плоскопараллельного или цилиндри-
ческого конденсатора переменной емкости. Емкость С плоского ЕД
определяется по формуле

где ε0 — электрическая постоянная; ε — относительная диэлектри-
ческая проницаемость среды между пластинами; S — площадь пла-
стин; δ — расстояние (зазор) между пластинами.
Поскольку емкость датчика зависит от трех параметров (S, δ, ε), то
существуют ЕД трех типов: 1) датчики с переменной площадью пере-
крытия пластин — для измерения линейных и угловых перемещений,
усилий; 2) датчики с переменным зазором δ, которые используются для
измерения малых перемещений, быстропеременных параметров, таких
как вибрация, ускорение; 3) датчики с переменной диэлектрической
проницаемостью среды ε — для измерения уровня, влажности, концен
трации, в охранной сигнализации и др. Статические характеристики
датчиков перемещения будут соответственно иметь вид
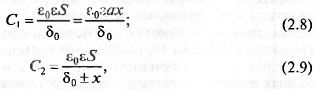
где а — ширина пластин конденсатора; х — измеряемое перемещение;
δ0 — начальный зазор.
Емкостные датчики с переменным воздушным зазором целесооб-
разно использовать для измерения малых линейных перемещений
(менее 1 мм), причем максимальное перемещение X не должно пре-
вышать 0,180. Это позволяет выбрать на статической характеристике
достаточно линейный участок. Емкостный датчик с переменной
площадью перекрытия пластин используется для измерения больших
линейных (более 1 см) и угловых (до 180°) перемещений.
Измерение емкости датчиков производится мостовым, резонансным
или импульсным методом. Для повышения чувствительности использу-
ют источники питания высокой частоты (от 400 Гц до нескольких мега-
герц). Преимуществами емкостных датчиков являются простота кон-
струкции, высокая чувствительность, малая инерционность, небольшой
вес и габариты, отсутствие подвижных контактов, простота приспособ-
ления формы конденсатора к различным задачам; недостатками —
низкая выходная мощность, нестабильность характеристик при измене-
нии параметров окружающей среды, необходимость тщательной экра-
нировки датчика и применения высокочастотного источника питания.
2.3 Индукционные датчики
Индукционный датчик относится к генераторным датчикам и
представляет собой устройство, состоящее из обмотки и магнитной
системы, осуществляющее преобразование контролируемой скорости
линейных или угловых перемещений в ЭДС. Принцип действия
основан на зависимости ЭДС, индуктируемой в обмотке при изме-
нении магнитного потока, пронизывающего ее витки, от скорости
его изменения в соответствии с законом электромагнитной индукции
Фарадея.
Эта ЭДС е определяется выражением

где W — число витков обмотки; Ф — магнитный поток.
Индукционные датчики подразделяются на две группы: в первом
случае обмотка перемещается относительно постоянного магнита,

совершая линейное Х или угловое φ перемещение, а во втором фер-
ромагнитная деталь (якорь или кольцо), механически связанная с
источником перемещений, перемещается относительно неподвижных
магнита и обмотки. У индукционного датчика скорости линейных
перемещений первого типа (рис. 2.2, а) обмотка, механически свя-
занная с подвижной частью устройства, перемещается относительно
магнитов; при этом ЭДС, индуктированная в обмотке, снимается
непосредственно с нее. У датчика угловых перемещений (рис. 2.2, б)
устройство аналогичное, но ЭДС снимается через коллектор. Маг-
нитный поток в обоих случаях постоянен и равен Ф. ЭДС Е на вы-
ходе датчика равна

где Кп — коэффициент пропорциональности, определяемый кон-
структивными параметрами датчика; х, φ — линейное и угловое пере-
мещение соответственно.
В индукционных датчиках второй группы (рис. 2.2, в, г) обмотка
и магнитопровод неподвижны, а кольцо или якорь, связанные меха-
нически с контролируемым устройством, являются подвижными.
В этих датчиках поток Ф не является постоянным, что обусловлено
изменением во времени магнитного сопротивления.
Наибольшее изменение магнитного потока
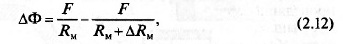
где F — намагничивающая сила; RM и RM+ ∆RM — крайние значения
магнитного сопротивления.
Чем больше скорость вращения, тем больше изменение магнит-
ного сопротивления и индуктированная ЭДС. Таким образом, вход-
ной величиной датчика является скорость вращения или перемеще-
ния, а выходной — индуктированная ЭДС (в случае углового пере-
мещения выходной величиной может быть частота электрического
сигнала в обмотке).
Индукционные датчики обеих групп имеют линейную статиче-
скую характеристику, представляющую собой зависимость ЭДС от
скорости перемещения. Достоинствами этих датчиков являются
сравнительно высокая точность и высокая чувствительность, что
позволяет использовать их непосредственно для измерения скоро-
сти без усилителей и других промежуточных элементов, а недо-
статками — влияние величины нагрузки на точность преобразо-
вания, а также наличие момента, действующего на вал, скорость
которого измеряется.
2.4. Вихретоковые датчики
Вихретоковый метод контроля основан на анализе взаимодей-
ствия внешнего электромагнитного поля с электромагнитным полем
вихревых токов, наводимых им в электропроводящем объекте кон-
троля. В качестве источника электромагнитного поля чаще всего
используется индуктивная катушка (одна или несколько), называе-
мая вихретоковым преобразователем (ВТП). Синусоидальный (или
импульсный) ток, действующий в катушках ВТП, создает электро-
магнитное поле, которое возбуждает вихревые токи в электропро-
водящем объекте. Электромагнитное поле вихревых токов воздей-
ствует на катушки преобразователя, наводя в них ЭДС или изменяя
их полное электрическое сопротивление. Регистрируя напряжение
на катушках или их сопротивление, получают информацию о свой-
ствах объекта или о положении преобразователя относительно него.
Особенность вихретокового контроля в том, что его можно прово-
дить без контакта преобразователя и объекта. Их взаимодействие
происходит на расстояниях, достаточных для свободного движения
преобразователя относительно объекта (от долей миллиметров до
нескольких миллиметров). Поэтому этими методами можно получать
хорошие результаты контроля даже при высоких скоростях движения
объектов.
Вихретоковые датчики (ВТД) используются для бесконтактного
измерения вибрации, перемещения и частоты вращения электро-
проводящих объектов. Они применяются для диагностики состояния
промышленных турбин, компрессоров, э