A площадь криволинейной трапеции;
+ B семейство интегральных кривых;
C криволинейная трапеция;
D угловой коэффициент касательной к графику функции.
Производная произведения двух функций
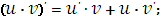
|
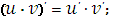
|
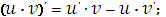
|
верного ответа нет.
Выберите верную трактовку производной функции
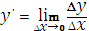
|
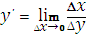
|
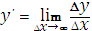
|
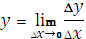
|
Найдите производную функци
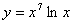
|
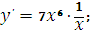
|
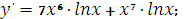
|
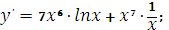
|
верного ответа нет.
Вычислите производную функци
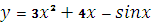
|
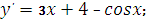
|
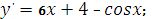
|
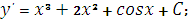
|

|
Дифференциал аргумента представляет собой
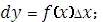
|

|
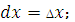
|
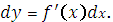
|
Дифференциал функции представляет собой
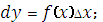
|
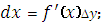
|
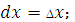
|
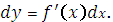
|
Для любой непрерывной функции всегда существует
+ A бесконечное множество первообразных;
B только одна первообразная;
C две различных первообразных, которые отличаются знаком, стоящим перед первым слагаемым;
D верного ответа нет.
Найдите общий вид первообразных для функци
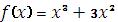
|
A
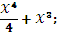
|
B верного ответа нет
+ C

|
Укажите функцию, для которой является первообразно
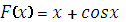
|
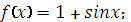
|
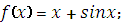
|
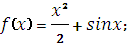
|
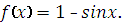
|
Какая из данных функций не является первообразной для функци
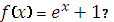
|
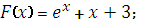
|
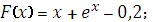
|
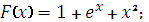
|
D верного ответа нет

|
5. Для функции f(x)= 5x4-3x2+1 найдите ее первообразную, если F(2)=20
A F(x)= 5x5-3x3-2
+ B F(x)= x5-x3+x-6
C F(x)= -x5+x3-x+1
D верного ответа нет.
6. Дана функция f(x)=x+3. Известно, что F(-2)=1, где F(x)- первообразная функции. Найдите F(-1).
A 2,5;
B 1;
+ C -2,5;
D 5.
7. Для функции f(x)= -10+x2, найдите первообразную, график которой проходит через точку M (4;-15)
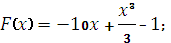
|
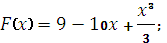
|
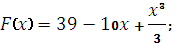
|
D верного ответа нет.
Неопределенным интегралом от функции f(x) называется
A первообразная функции f(x)
B функция, производная которой равна функции f(x)
+ C множество всех первообразных
D площадь криволинейной трапеции, ограниченной сверху функцией f(x)
2. Неопределенный интеграл от функции f(x) это …

|
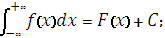
|

|
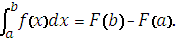
|
3. Геометрически неопределенный интеграл представляет собой …
A площадь криволинейной трапеции;
+ B семейство интегральных кривых;
C криволинейную трапецию;
D угловой коэффициент касательной к графику функции.
Какой из методов применим для решения интеграла
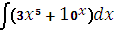
|
A метод замены переменной;
+B метод интегрирования по частям;
C метод непосредственного интегрирования;
D верного ответа нет.
Какой из методов применим для решения интеграла
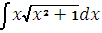
|
+A метод замены переменной;
B метод интегрирования по частям;
C метод непосредственного интегрирования;
D верного ответа нет.
6. Интегрирование – это …
A операция нахождения производной по заданной функции;
+B операция нахождения первообразной по заданной производной или дифференциалу;
C верного ответа нет.
Укажите целесообразную подстановку для отыскания интеграла
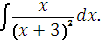
|
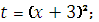
|
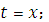
|
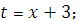
|
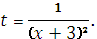
|
Укажите целесообразную подстановку для отыскания интеграла
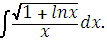
|
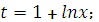
|
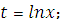
|
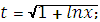
|

|
9. Определенный интеграл – это …
A совокупность всех первообразных F(x)+C;
+ B предел, к которому стремится интегральная сумма при стремлении к нулю длины наибольшего частичного интервала
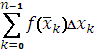
|
C предел отношения приращения функции к приращению ее аргумента при стремлении последнего к нул
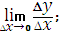
|
D верного ответа нет.
10. Определенный интеграл от функции f(x)это …
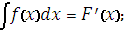
|
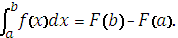
|
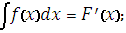
|
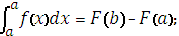
|
Какие из свойств определенного интеграла верные?

|
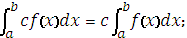
|
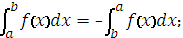
|
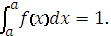
|
12. Формула Ньютона – Лейбница:
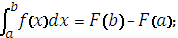
|
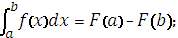
|
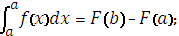
|
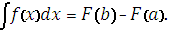
|
Вычислите интеграл
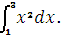
|
A 9;
B 26/3;
+ C 8;
D 0.
Вычислите интеграл
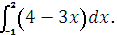
|
+ A -9;
B -3,5;
C 7,5;
D 1.
При каком значении верно равенство?
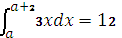
|
A 1;
+ B 4;
C -1;
D 0.