5,91732 13,5681 10,1369 12,0409 13,3652 5,74917
14,6142 16,1241 15,9044 10,1954 9,8052 8,0279
9,56704 12,7445 6,93781 13,0821 8,51345 6,05509
6,67886 7,00127 10,6225 8,60706 10,4542 7,17316
9,76469 8,05324 8,60399 12,1798 11,816 12,9114
8,67782 9,76389 15,2546 6,14625 9,78521 12,239
8,00063 9,1715 11,6456 11,9813 16,9382 4,57724
10,2874 12,4684 11,7605 12,2355 8,84734 10,3525
5,76842 4,97502 7,93101 12,7332 12,9146 18,3794
16,3878 3,77045 11,2058 13,617 15,9688 9,63555
10,3911 4,0522 6,72052 7,85879 7,02947 9,36878
15,5732 8,13941 6,48565 10,5805 11,0499 5,73129
9,91754 10,4424 16,0757 15,7639 1,79992 1,31334
6,2902 8,23677 5,27401 5,63055 14,9883 11,4898
6,74004 6,48766 9,04737 9,57965 9,50583 13,0075
7,62863 12,9128 9,28577 7,69982 7,26289 16,2481
11,4312 13,0762 11,0002 8,09916 6,308 14,4091
11,1474 13,5127 5,05696 14,2908 9,90656 10,3138
12,4905 7,66372 10,5641 13,5088 11,0778 12,094
5,75424 12,2517 9,44279 5,8969 4,70238 10,7459
Рис. 5.4. Модельные выборки «Кох» для проверки равенства дисперсий
с помощью критерия Кохрена
Параметры выборки «Бар»
Параметры выборки «Кох»
Рис. 5.5. Параметры модельных выборок «Бар» и «Кох»
Традиционный для системы STATGRAPHICS Plus for Windows алгоритм, который будет одинаков для обоих критериев проверки. Последовательно щелкаем левой кнопкой мыши на Compare (Сравнение) / Multiple Samples (Несколько выборок) / Multiple-Sample Comparison (Сравнение параметров нескольких выборок). На выпадающем меню Multiple-Sample Comparison сразу нажимаем ОК, далее на контекстном меню с таким же названием (рис.5.5) сразу выделяем подлежащие тестированию выборки (RAND1, RAND2, RAND3, RAND4), нажимаем кнопку (Samples) и ОК. Не обращая внимание на появившиеся таблицы и графики, левой кнопкой мыши щёлкаем по второй слева иконке 
Tabular Options (Таблица выполняемых операций) в нижнем ряду, в выпадающем меню Tabular Options (рис.5.7) выделяем Variance Check (Тестирование дисперсий) и OK. Выделение одной опции соответствует нашей
Рис. 5.6. Таблица, подготовленная для выбора данных для последующего
статистического анализа
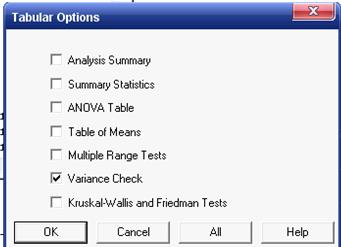
Рис. 5.7. Меню с предлагаемыми функциями статистического анализа.
задаче (проверка равенства дисперсий). Если Вас ещё интересуют параметры анализируемых выборок, то на таблице (рис.5.7) выделите дополнительно Summary Statistics (Параметры выборок). Рис. 5.5 как раз получен после этих процедур. Мы ограничиваемся анализом равенства дисперсий (рис.5.7, 5.8, 5.9).
Здесь (рис.5.8 и 5.9) надо анализировать не значения критериев проверки (их значения приведены после наименования критериев), а вероятности (p-Value) принятия нулевой гипотезы о равенстве дисперсий. Видно (рис.5.8), что вероятность принятия этой гипотезы, полученная в результате сравнения дисперсий по критерию Бартлетта (Bartlett's test) ничтожна (0,00000208715). О равноточности измерений выборок «Бар» не может идти речь.
Рис. 5.8. Результаты сравнения дисперсий для выборок «Бар»
Аналогичным образом реализуем алгоритм сравнения дисперсии для выборок «Кох» (рис.5.9).
Рис. 5.9. Результаты сравнения дисперсий для выборок «Кох»
Видно, что оба критерия проверки указывают на очень высокую вероятность принятия нулевой гипотезы о равенстве дисперсий (p-Value равны соответственно 0,54 и 0,758) для выборок «Кох», причём критерий Кохрена (Cochran's test: 0,235193) очень близок к таковому из примера 5.3 [1] (G эмп=0,208).
Второй вариант алгоритма проверки равенства дисперсий состоит из следующих шагов: создание электронной таблицы с тестируемыми выборками; далее последовательно щелкаем левой кнопкой мыши на SnapStat!! (Кнопка суммарного статистического анализа) / Multiple Sample Comparison (Сравнение нескольких выборок) / Multiple Data Columns (Колонки для нескольких выборок) / OK / Выделение анализируемых выборок по типу рис.5.5 / Samples (Тестируемые выборки) / OK /. Выпадает окно с результатами расширенного статистического анализ, в том числе и с результатами тестирования равенства дисперсий. Но здесь в отличие от предыдущего алгоритма (рис.5.8 и 5.9) тестирование проведено по одному из критериев проверки.
Для перехода к другим критериям проверки необходимо после создания электронной таблицы последовательно щёлкать по Edit (Редактирование) / Snap Stat Options (Опции суммарного статистического анализа) / Comparisons (Сравнение) / Выбрать требуемый тест проверки согласия: Cochran's Test, или Bartlett's Test, или Hartley's Test, или Levense's Test. Далее не забыть щёлкнуть по кнопке «Применить» / ОК. В результатах анализа появится значение заказанного эмпирического критерия проверки и вероятность принятия нулевой гипотезы.
6 СРАВНЕНИЕ ДВУХ СРЕДНИХ ЗНАЧЕНИЙ НОРМАЛЬНО РАСПРЕДЕЛЕННЫХ СОВОКУПНОСТЕЙ
6.1. Цель занятия
Практическое освоение правил сравнения двух средних, полученных для разных выборок, а также правил объединения результатов этих выборок и оценки взвешенного среднего.
6.2. Сравнение двух средних по критерию Стьюдента. Если, как это описано в примере 6.1 [1], известны объёмы выборок и их средние квадратические отклонения, то создавать электронную таблицу не надо. Сразу приступаем к процедуре сравнения средних. Для этого последовательно щёлкаем левой кнопкой мыши по Compare (Сравнение) / Two Samples (Две выборки) / Hypothesis Tests (Тестирование гипотез) / OK.
В результате имеем таблицу Hypothesis Tests (Compare) (рис. 6.1), в которую вводим исходные данные (средние, СКО и объёмы выборок) из примера 6.1 [1]. Указываем, что сравнивать надо два средних Sample 1 Mean и Sample 2 Mean из нормально распределённой совокупности (Normal Means), СКО (Sample 1 Sigma) и объём (Sample 1 Size) первой выборки, СКО (Sample 2 Sigma) и объём второй выборки (Sample 2 Size), далее ОК.
Рис. 6.1. Таблица для ввода исходных данных при сравнении равенства двух средних по критерию Стьюдента
Результаты статистического анализа. Раскрываем таблицу с результатами статистического анализа двойным щелчком левой кнопкой мыши на поле таблицы (рис.6.2.). Здесь сразу надо обратить внимание на вероятность принятия нулевой гипотезы (P-Value = 0,00331498), которая практически равна нулю, а, следовательно, разница между средними значима на уровне значимости 0,05. Это совпадает с выводом в примере 6.1 [1]. Обращает на себя внимание приме-
Рис. 6.2. Результаты проверки гипотезы о равенстве двух средних
(Дисперсии предполагаются равными)
чание о том, что в процессе тестирования гипотезы предполагалось равенство дисперсий (Equal variances assumed). Система позволяет сравнивать средние и в случае неравенства результатов измерений в выборках. Для этого достаточно щёлкнуть правой кнопкой на поле таблицы и в выпадающем меню убрать галочку Assume Equal Sigmas, далее ОК. Результаты анализа на рис.6.3.
Рис. 6.3. Результаты проверки гипотезы о равенстве двух средних.
(Дисперсии предполагаются неравными)
Вероятность (0, 22) принятия нулевой гипотезы в этом случае близка к критической (0,05)!
7 КОРРЕЛЯЦИОННЫЙ АНАЛИЗ ДЛЯ СЛУЧАЯ
ЛИНЕЙНОЙ ПАРНОЙ СВЯЗИ
7.1. Цель занятия
Практическое освоение правил оценки коэффициента корреляции и получения параметров уравнения регрессии в случае линейной парной связи результатов совместных измерений.
Выполнить корреляционный анализ (оценить коэффициент корреляции) в системе STATGRAPHICS Plus for Windows можно по разным алгоритмам. Ниже рассмотрен порядок проведения корреляционного анализа, который позволяет получить выходные данные, рассмотренные в примере 7.1
7.2. Создание электронной таблицы с данными для статистического анализа.
Исходное положение: Рабочее окно системы STATGRAPHICS Plus for Windows. Для проведения корреляционного анализа результатов совместных измерений заполняем две колонки (рис. 7.1), (пример 7.1 из [1]).
Рис. 7.1. Фрагмент электронной таблицы, подготовленной для
корреляционного анализа
Статистическому анализу результатов совместных измерений обязательно предшествует графический анализ, то есть построение графика – поля корреляции, в данном случае, d =f(U). Это можно сделать, как это описано в разделе 8 « Регрессионный анализ результатов совместных измерений для случая линейной модели».Но можно сразу приступить к корреляционному анализу, так как система STATGRAPHICS Plus for Windows сопровождает статистический анализ графическим анализом.
7.3. Статистический анализ
Последовательно щёлкаем левой кнопкой мыши по Relate (В данном контексте это выяснение отношений между зависимыми и независимыми переменными) / Simple Regression (Простая регрессия). В выпадающей таблице (рис.7.2) отмечаем, какие переменные откладываем по оси Y (в данном случае Твёрдость, НВ) и какие по оси X (Величина сигнала, мВ) и далее нажимаем кнопку OK.
Рис. 7.2. Таблица, подготовленная для выбора данных для