Под идеальным газом понимают воображаемый газ, в котором отсутствуют силы притяжения между молекулами, а собственный объем молекул очень мал по сравнению с объемом межмолекулярного пространства. В действительно существующих газах при высоких температурах и малых давлениях можно пренебречь силами притяжения между молекулами и объемом самих молекул. Поэтому такие газы можно считать идеальными.
В тех газах, которые находятся в состояниях, достаточно близких к сжижению, нельзя пренебречь силами притяжения между молекулами и объемом последних. Такие газы нельзя отнести к идеальным, и их называют реальными газами.
Основное уравнение кинетической теории газов имеет вид:
 , (2.1)
, (2.1)
где  - давление идеального газа;
- давление идеального газа;
n - число молекул в 1 м3 газа (концентрация молекул);
m - масса одной молекулы;
w - средняя квадратичная скорость поступательного движения молекул;
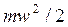 - средняя кинетическая энергия поступательного движения одной молекулы.
- средняя кинетическая энергия поступательного движения одной молекулы.
Таким образом, основное уравнение кинетической теории газов устанавливает связь между давлением газа, средней кинетической энергией поступательного движения молекул и их концентрацией. Основные зависимости, характеризующие соотношение между параметрами идеального газа при некоторых вполне определенных условиях изменения его состояния, легко получаются из основного уравнения кинетической теории газов. До этого они были получены экспериментальным путем.
Так, если температура газа не изменяется (T=const), то давление газа и его объем связаны следующей зависимостью (закон Бойля-Мариотта);
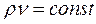 (2.2)
(2.2)
Если давление газа остается постоянным (P=const), то соотношение между удельным объемом газа и его абсолютной температурой подчиняется закону Гей-Люссака;
 (2.3)
(2.3)
или
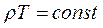 (2.4)
(2.4)
Для газов, взятых при одинаковых температурах и давлениях, имеет место следующая зависимость, полученная на основе закона Авогадро:
 , (2.5)
, (2.5)
где μ - молекулярная масса газа;
ρ - плотность вещества.
Так как ρ=1/ν
 (2.6)
(2.6)
Величина μν представляет собой объем килограмм-молекулы или киломоля (кмоль) газа.
Принято относить 1м3 газа к нормальным условиям, при которых рабочее вещество находится под давлением:
Р= 101325 Па и Т= 273,15 К (760 мм рт.ст. и 0°С).
Объем 1 кмоля всех идеальных газов равен 22,4136 м3/кмоль при нормальных условиях.
Плотность газа при нормальных условиях определяется из равенства:
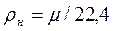
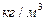 (2.7)
(2.7)
Пользуясь этой формулой, можно найти удельный объем любого газа при нормальных условиях:

 (2.8)
(2.8)
Характеристическое уравнение идеального газа или уравнение состояния связывает между собой основные параметры состояния – давление, объем и температуру – и может быть представлено следующими уравнениями:
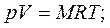 (2.9)
(2.9)
 (2.10)
(2.10)
 (2.11)
(2.11)
где Р – абсолютное давление газа в Па;
V- объем газа в м3:
M- масса газа в кг;
v- удельный объем газа в м3/кг;
 - объем одного кмоля газа в м3/кмоль;
- объем одного кмоля газа в м3/кмоль;
R- газовая постоянная для 1 кг газа в Дж/(кг·К);
Т- абсолютная температура, К:
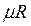 - универсальная газовая постоянная 1 кмоля газа в Дж/(кмоль·К).
- универсальная газовая постоянная 1 кмоля газа в Дж/(кмоль·К).
Каждое из этих уравнений отличается от другого лишь тем, что относится к различным массам газа: первое – к М кг; второе - к 1 кг, третье – к 1 кмолю газа.
Численное значение универсальной газовой постоянной легко получить из уравнения (2.11) при подстановке значений входящих в него величин при нормальных условиях:



Газовую постоянную, отнесенную к 1 кг газа, определяют из уравнения

 (2.12)
(2.12)
Где μ - масса 1 кмоля газа в кг (численно равная молекулярной массе газа).
Пользуясь характеристическим уравнением для двух различных состояний какого-либо газа, можно получить выражение для определения любого параметра при переходе от одного состояния к другому, если значения остальных параметров известны:

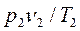 (2.13)
(2.13)

 (2.14)
(2.14)
Если объем газа известен, уравнение (2.14) представляют в виде:
 (2.15)
(2.15)
В правой части уравнения все величины взяты при нормальных условиях, а в левой – при произвольных значениях давления и температуры.
Уравнение можно переписать следующим образом:

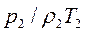
Следовательно,

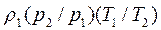 (2.16)
(2.16)
Данное уравнение позволяет найти плотность газа при любых условиях, если значение его для определенных условий известно.
Задачи
2.1. Какой объем занимает 1 кг азота при температуре 70 0С
и давлении 0.2 МПа? Ответ: V=0.5 м3.
2.2. Плотность воздуха при нормальных условиях rн=1.293 кг/м3.
Чему равна плотность воздуха при давлении Р=1.5 МПа и температуре t=20 0С.
Ответ: r=17.82 кг/м3.
2.3. Во сколько раз объем определенной массы газа при температуре t= -20 0С меньше, чем при t=+20 0С, если давление в обоих случаях одинаковое?
При постоянном давлении объем газа изменяется по уравнению(2.3):
V/T=const или V2/V1=T2/T1,
следовательно,
V2/V1=(273+20)/(273-20)=1.16.
Ответ: в 1.16 раза.
2.4. В воздухоподогреватель парового котла подается вентилятором 130 000 м3/ч воздуха при температуре 30 0С.
Определить объемный расход воздуха на выходе из воздухоподогревателя, если он нагревается до 400 0С при постоянном давлении.
Ответ: V=288 700 м3/ч.
2.5. Найти массу 5 м3 водорода,5 м3 кислорода и 5 м3 углекислоты при давлении 0.6 МПа и температуре 100 0С.
Решение:
Воспользуемся уравнением идеального газа для произвольного количества газа
РV=МRT.
Следовательно,
M=РV/RT=0.6·106·5/R·373=8042.8/R.
Значения газовых постоянных берем из табл.IV(см. приложения):
RH2=4124 Дж/(кг К); RO2=259.8 Дж/(кг К);
RCO2=188.9 Дж/(кг К).
Тогда
MH2=8042.8/24124=1.95 кг;
MO2=8042.8/259.8=30.9 кг;
MCO2=8042.8/188.9=42.6 кг.
Ответ: MH2=1.95 кг; MO2= 30.9 кг; MCO2 =42.6 кг.
2.6. В цилиндре диаметром 0.6 м содержится 0.41 м3 воздуха при Р=0.25 МПа и t1=35 0С.
До какой температуры должен нагреваться воздух при постоянном давлении, чтобы движущийся без трения поршень поднялся на 0.4 м?
Ответ: t2=117.6 0С.
2.9. В цилиндрическом сосуде, имеющем d=0.6 м и высоту h=2.4 м, находится воздух при температуре 18 0С. Давление воздуха составляет 0.765 МПа. Барометрическое давление (приведенное к нулю) равно 101858 Па. Определить массу воздуха в сосуде.
Ответ: М=7.04 кг.
2.10. Баллон с кислородом емкостью 20 л находится под давлением 10 МПа при 15 0С. После израсходования части кислорода давление понизилось до 7.6 МПа, а температура упала до 10 0С.
Определить массу израсходованного кислорода.
Решение:
Из уравнения состояния идеального газа
M=РV/RT.
Следовательно, до расходования кислорода масса его составляла
М1=10·106·0.02/259.8·288=2.673 кг,
а после израсходования
М2=7.6·106·0.02/259.8·283=2.067 кг,
таким образом, расход кислорода
2.673-2.067=0.606 кг.
Ответ: М1-М2=0.606 кг
2.11. Резервуар объемом 4 м3 заполнен углекислым газом. Найти массу и силу тяжести (вес) газа в резервуаре, если избыточное давление газа Рман =40 кПа, температура его t=80 0С, а барометрическое давление воздуха В=102.4 кПа.
Ответ: М=8.64 кг; G=84.8 H.
2.12. Сосуд емкостью V=10 м3 заполнен 25 кг углекислоты. Определить абсолютное давление в сосуде, если температура в нем t=27 0C.
Решение:
Из уравнения состояния идеального газа имеем
Рабс =MRT/V=25·8314·300/44·10=141 700 Па=141.7 кПа.
Ответ: Рабс =141.7 кПа
2.13. Баллон емкостью 0.9 м3 заполнен воздухом при температуре 17 0С, присоединенный к нему вакууметр показывает разрежение Рвак = 80 кПа. Определить массу воздуха в баллоне, если показание барометра равно 98.7 кПа.
Ответ: М=0.2018 кг.
2.14. Определить подъемную силу воздушного шара, наполненного водородом, если объем его на поверхности земли равен 1 м3 при давлении р=100 кПа и температуре t=15 0C.
Решение:
На поверхности земли подъемная сила воздушного шара, наполненного водородом, равна разности сил тяжести (весов) воздуха и водорода в объеме шара:
G=Gвозд-GH2=(Mвоздg-МH2) g=gV(rвозд-rН2),
где g=9.81 м/с2-ускорение свободного падения.
Значения плотностей воздуха и водорода могут быть определены из уравнения состояния
Рv=RT, откуда 1/v=r=Р/RT.
Значения газовых постоянных могут быть легко вычислены или взяты из табл. IV (см. приложения); Rвозд=287 Дж/(кг К); RH2=4124 Дж/(кг К).
Так как давление водорода и воздуха равно 0.1 МПа, то
r возд=0.1·106/287·288=1.210 кг/м3;
r H2=0.1·106/4124·288=0.084 кг/м3.
Следовательно, подъемная сила шара
DG=gV(rвозд-rН2)=9.81·1· (1.210-0.084)=11.1 Н.
2.15. Газохранилище объемом V=100 м3 (Рис 2.1) наполнено газом коксовых печей.
Рис. 2.1
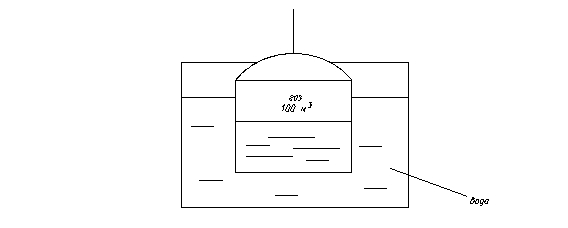
Определить массу газа в газохранилище, если t=200С, В=100 кПа, а показание манометра, установленного на газохранилище р=133.3 кПа. Газовую постоянную коксового газа принять равной 721 Дж/(кг К).
Ответ: М=47.6 кг.
2.16. Воздух, заключенный в баллон емкостью 0.9 м3, выпускают в атмосферу. Температура его вначале равна 27 0С. Найти массу выпущенного воздуха, если начальное давление в баллоне составляло 9.32 МПа, после выпуска -4.22 МПа, а температура воздуха снизилась до 17 0С.
Ответ: 51.8 кг.
2.17. Дутьевой вентилятор подает в топку парового котла 102000 м3/ч воздуха при температуре 300 0С и давлении 20.7 кПа. Барометрическое давление воздуха в помещении В=100.7 кПа.
Определить часовую производительность вентилятора в м3 (при нормальных условиях).
Ответ: Q=48 940 м3/ч.
Газовые смеси
Состав газовой смеси определяется количеством каждого из газов, входящих в смесь, и может быть задан массовыми или объемными долями.
Массовая доля определяется отношением массы отдельного газа, входящего в смесь, к массе всей смеси:
m1=M1/M, m2=M2/M, mN=MN/M,
где M1, M2, M3, MN – массы отдельных газов и M – масса всей смеси.
Объемной долей газа называют отношение объема каждого компонента, входящего в смесь, к объему всей газовой смеси при условии, что объем каждого компонента отнесен к давлению и температуре смеси (приведенный объем):
r1=V1/V, r2=V2/V, rN=VN/V,
где V1, V2, VN – приведенные объемы компонентов газов, входящих в смесь;
V – общий объем газовой смеси.
Очевидно, что
M1+M2+M3+…..+MN=М;
m1+m2+m3+…..+mN=1,
а также
V1+V2+V3+…..+VN=V;
r1+r2+r3+…..+rN=1.
Для перевода массовых долей в объемные пользуются формулой:
 (3.1)
(3.1)
Объемные доли переводят в массовые по формуле:
 (3.2)
(3.2)
Плотность смеси определяют из выражения:
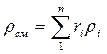 ,
,  (3.3)
(3.3)
или, если известен массовый состав, по формуле:
 ,
,  (3.4)
(3.4)
Удельный объем смеси представляет величину, обратную ρсм; поэтому, если дан объемный состав смеси, то:
 ,
,  (3.5)
(3.5)
Если же известен массовый состав, то:
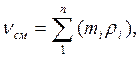
 (3.6)
(3.6)
Из уравнения (26) легко получить значение так называемой кажущейся молекулярной массы газовой смеси:
 (3.7)
(3.7)
или через массовый состав:
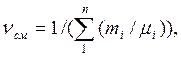 (3.8)
(3.8)
Газовую постоянную смеси газов (Rсм) можно выразить или через газовые постоянные отдельных компонентов, входящих в смесь, или через кажущуюся молекулярную массу смеси:

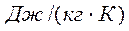 (3.9)
(3.9)
или
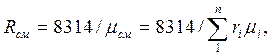
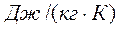 (3.10)
(3.10)
Связь между давлением газовой смеси и парциальными давлениями отдельных компонентов, входящих в смесь, устанавливается следующей зависимостью (закон Дальтона), легко получаемой из основного уравнения кинетической теории газов:
Р =р1+р2+р3+ …. +рN, (3.11)
где Р – общее давление газовой смеси;
р1, р2, р3, рN – парциальное давление отдельных компонентов, входящих в смесь.
Парциальные давления определяются проще всего, если известны объемные доли отдельных компонентов, входящих в смесь;
р1=рr1, р2=рr2 и т.д.
или вообще
рi=рri, (3.12)
где рi – парциальное давление любого газа, входящего в смесь:
рi=mi(Ri/Rсм)р.
Задачи
3.1. Атмосферный воздух имеет примерно следующий массовый состав:
mO2=23.2%; mN2=76.8%. Определить объемный состав воздуха, его газовую постоянную, кажущуюся молекулярную массу и парциальные давления кислорода и азота, если давление воздуха по барометру В=101 325 Па.
Решение:
По уравнению (3.1) получаем
rO2=(mO2/mO2)/(mO2/mO2+mN2/mN2)=(23.2/32)/(23.2/32+76.8/28.02)=0.2;
rN2=(mN2/mN2)/(mO2/mO2+mN2/mN2)=(76.8/28.02)/(23.2/32+76.8/28.02) =0.79.
Газовую постоянную воздуха находим по уравнению (3.9):
Rсм=Sm i R i=mO2RO2+mN2RN2=0.232·260+0.768·295=287 Дж/кг К.
Кажущуюся молекулярную массу смеси определяем из уравнения (3.7)
mсм=Sr i m i=rO2mO2+rN2mN2=0.21·32+0.79·28.02=28.9
или из уравнения (3.10)
Rсм=8314/mcм.
Отсюда
mcм=8314/Rсм=8314/287=28.9
Парциальные давления получим из уравнения (3.12) р i =r i p,
следовательно,
рО2= rO2 Р=0.21∙101 325=21 278 Па; рN2=rN2p=0.79∙101 325=80 047 Па.
Ответ: rO2=0.2; rN2=0.79; Rсм=287Дж/кгК;mcм=28.9; рО2=21 278 Па; рN2=80 047 Па
3.2. В 1 м3 сухого воздуха содержится примерно 0.21 м3 кислорода и 0.79 м3 азота. Определить массовый состав воздуха, его газовую постоянную и парциальные давления кислорода и азота.
Ответ:mO2=0.232; N2=0.768; R=287 Дж/кгК; pN2=0.79Рсм, Па; pO2=0.21Рсм.Па
3.3. Смесь газов состоит из водорода и окиси углерода. Массовая доля водорода mH2=0.067%.
Найти газовую постоянную смеси и ее удельный объем при нормальных условиях.
Решение:
Из уравнения (3.9)
Rсм = Sm i R i =m1 R1+m2 R2=0.0667∙4124+0.9333∙296.8=552 Дж/кгК.
Удельный объем газовой смеси получим из уравнения состояния идеального газа vн = RTн/pн=552∙273/101325=1.49 м3/кг.
Ответ: Rсм =552 Дж/кгК; vн =1.49 м3/кг.
3.4. Определить газовую постоянную смеси газов, состоящей из 1 м3 генераторного газа и 1.5 м3 воздуха, взятых при нормальных условиях, и найти парциальные давления составляющих смеси. Плотность генераторного газа r принять равной 1.2 кг/м3.
Ответ: Rсм=295 Дж/кгК; pгг=0.4Рсм; рвозд=0.6Рсм.
3.5. Объемный состав сухих продуктов сгорания топлива (не содержащих водяных паров) следующий: СО2=12.3%;О2=7.2%;N2=80.5%. Найти кажущуюся молекулярную массу и газовую постоянную, а также плотность и удельный объем продуктов сгорания при В=100кПа и t=800 0C.
Ответ: mсм=30.3; Rсм=274 Дж/кгК; v=2.94 м3/кг; rсм=0.34 кг/м3.
3.6. Найти газовую постоянную, удельный объем газовой смеси и парциальные давления ее составляющих, если объемный состав смеси следующий: СО2=12%; CO=1%; H2O=6%; O2=7%; N2=74%; а общее давление ее р=100 кПа.
Ответ: Rсм=281 Дж/(кг К); v=0.76 м3/кг; рСО2=12000 Па.
3.7. Массовый состав смеси следующий: СО2=18%; O2=12%; N2=70%. До какого давления нужно сжать 8 кг этой смеси, находящейся при нормальных условиях, чтобы при t=180 0С она занимала объем, равный 4 м3.
Ответ: Р=0.24 МПа.
3.8. Определить массовый состав газовой смеси, состоящей из углекислого газа и азота, если известно, что парциальное давление углекислого газа рСО2=120 кПа, а давление смеси рсм=300 кПа.
Ответ: mCO2=0.512; mN2=0.488.
3.9. Газовая смесь имеет следующий массовый состав: СО2=12%; О2=8%; N2=80%. До какого давления нужно сжать эту смесь, находящуюся при нормальных условиях, чтобы плотность ее составляла 1.6 кг/м3?
Ответ: До 0,213 МПа.
Теплоемкость газов
Теплоемкостью называют количество теплоты, которое необходимо сообщить телу (газу), чтобы повысить температуру какой-либо количественной единицы на 1°С
За единицу количества энергии в системе СИ применяют джоуль (Дж). В качестве тепловой единицы 1 Дж представляет собой такое ее количество, которое появляется в результате превращения механической работы 1 Дж в теплоту. В качестве единицы механической энергии джоуль представляет собой работу, совершаемую силой, равной 1 ньютону при перемещении ею тела на расстояние 1 м в направлении действия силы (1 Дж =Н·м=1 кг·м2/с2).
В зависимости от выбранной количественной единицы вещества различают мольную теплоемкость µc – кДж/(кмоль·К), массовую теплоемкость c – кДж/(кг·К) и объемную теплоемкость c’– кДж/(м3·К).
Удобнее всего иметь величину мольной теплоемкости. Тогда массовая теплоемкость
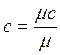 , (4.1)
, (4.1)
а объемная теплоемкость
 . (4.2)
. (4.2)
Объемная и массовая теплоемкости связаны между собой зависимостью

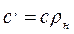
где ρн - плотность газа при нормальных условиях.
Теплоемкость газа зависит от его температуры. По этому признаку различают среднюю и истинную теплоемкость.
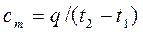 , (4.3)
, (4.3)
Сm – представляет собой среднюю теплоемкость в пределах (t2-t1). Предел этого отношения, когда разность температур стремится к нулю, называется истинной теплоемкостью

Таким образом, различают истинную и среднюю теплоемкости:
а) мольную – в процессах при постоянном объеме ( и
и  ) и постоянном давлении (
) и постоянном давлении ( и
и  );
);
б) массовую – в процессах при постоянном объеме (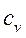 и
и 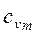 ) и постоянном давлении (
) и постоянном давлении ( и
и  );
);
в) объемную – в процессах при постоянном объеме (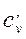 и
и  ) и постоянном давлении (
) и постоянном давлении ( и
и  );
);
Между мольными теплоемкостями при постоянном давлении и постоянном объеме существует следующая зависимость:
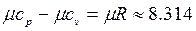
 (4.4)
(4.4)
Для приближенных расчетов при невысоких температурах можно принимать следующие значения мольных теплоемкостей (табл. 4.1).
Таблица 4.1.
Приближенные значения мольных теплоемкостей
| Газы | Теплоемкость в кДж/(кмоль·К) | |
 v v
|  p p
| |
| Одноатомные | 12,56 | 20,93 |
| Двухатомные | 20,93 | 29,31 |
| Трех- и многоатомные | 29,31 | 37,68 |
В технической термодинамике большое значение имеет отношение теплоемкостей при постоянном давлении и постоянном объеме, обозначаемое буквой k:
Для одноатомных газов k =1,67; для двухатомных газов k =1,4; для трех- и многоатомных газов k =1,29.
Количество теплоты, которое необходимо затратить в процессе нагревания 1 кг газа в интервале температур от t 1 до t 2,
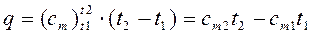 , (4.5)
, (4.5)
где  и
и  - средние теплоемкости в пределах 0°-
- средние теплоемкости в пределах 0°-  и 0°-
и 0°-  .
.
Для определения количества теплоты, затрачиваемой в процессах при постоянном давлении и постоянном объеме использовать формулы (4.6), (4.7)
 (4.6)
(4.6)
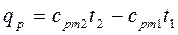 (4.7)
(4.7)
Если в процессе участвуют  кг и
кг и  м3 газа, то:
м3 газа, то:
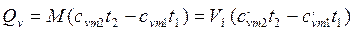 (4.8)
(4.8)  ; (4.9)
; (4.9)
Нелинейную зависимость истинной теплоемкости от температуры представляют обычно уравнением вида:
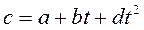 ,
,
где а, b и d – величины постоянные для данного газа.
При замене нелинейной зависимости линейной, истинная теплоемкость примет вид:
 ,
,
а средняя теплоемкость в пределах 0° - 
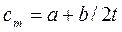 (4.10)
(4.10)
В табл. 4.2 приведены интерполяционные формулы для истинных и средних мольных теплоемкостей при постоянном давлении, а в табл. 4.3 - для средних массовых объемных теплоемкостей при постоянном объеме.
Теплоемкость газовой смеси:
массовая: 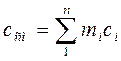 (4.11)
(4.11)
объемная:  (4.12)
(4.12)
мольная: 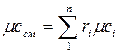 (4.13)
(4.13)
Таблица 4.2.
Интерполяционные формулы для истинных и средних мольных теплоемкостей газов
| Газ | Мольная теплоемкость при 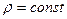 в кДж/(кмоль·К) в кДж/(кмоль·К)
| |
| Истинная | средняя | |
| В пределах 0 - 1000°С | ||
| О2 | 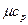 =29,5802 + 0,0069706 t =29,5802 + 0,0069706 t
|  =29,2080 + 0,0040717 t =29,2080 + 0,0040717 t
|
| N2 | 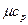 =28,5372 + 0,0053905 t =28,5372 + 0,0053905 t
|  =28,7340 + 0,0023488 t =28,7340 + 0,0023488 t
|
| СО | 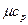 =28,7395 + 0,0058862 t =28,7395 + 0,0058862 t
|  =28,8563 + 0,0026808 t =28,8563 + 0,0026808 t
|
| Воздух | 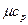 =28,7558 + 0,0057208 t =28,7558 + 0,0057208 t
|  =28,8270 + 0,0027080 t =28,8270 + 0,0027080 t
|
| Н2О | 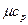 =32,8367 + 0,0116611 t =32,8367 + 0,0116611 t
|  =33,1494 + 0,0052749 t =33,1494 + 0,0052749 t
|
| SО2 | 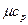 =42,8728 + 0,0132043 t =42,8728 + 0,0132043 t
|  =40,4386 + 0,0099562 t =40,4386 + 0,0099562 t
|
| В пределах 0 - 1500°С | ||
| H2 | 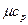 =28,3446 + 0,0031518 t =28,3446 + 0,0031518 t
|  =28,7210 + 0,0012008 t =28,7210 + 0,0012008 t
|
| CO2 | 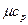 =41,3597 + 0,0144985 t =41,3597 + 0,0144985 t
|  =38,3955 + 0,0105838 t =38,3955 + 0,0105838 t
|
| В пределах 1000 - 2700°С | ||
| O2 | 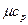 =33,8603 + 0,0021951 t =33,8603 + 0,0021951 t
|  =31,5731 + 0,0017572 t =31,5731 + 0,0017572 t
|
| N2 | 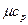 =32,7466 + 0,0016517 t =32,7466 + 0,0016517 t
|  =29,7815 + 0,0016835 t =29,7815 + 0,0016835 t
|
| CO | 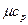 =33,6991 + 0,0013406 t =33,6991 + 0,0013406 t
|  =30,4242 + 0,0015579 t =30,4242 + 0,0015579 t
|
| Воздух | 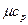 =32,9564 + 0,0017806 t =32,9564 + 0,0017806 t
|  =30,1533 + 0,0016973 t =30,1533 + 0,0016973 t
|
| H2О | 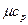 =40,2393 + 0,0059854 t =40,2393 + 0,0059854 t
|  =34,5118 + 0,0045979 t =34,5118 + 0,0045979 t
|
| В пределах 1500 - 3000°С | ||
| H2 | 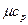 =31,0079 + 0,0020243 t =31,0079 + 0,0020243 t
|  =31,5731 + 0,0017572 t =31,5731 + 0,0017572 t
|
| СО2 | 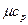 =56,8768 + 0,0021738 t =56,8768 + 0,0021738 t
|  =48,4534 + 0,0030032 t =48,4534 + 0,0030032 t
|
Таблица 4.3.
Интерполяционные формулы
для средних массовых и объемных теплоемкостей газов
| Газ | Теплоемкость в кДж/(кг·К) | |
| Массовая | объемная | |
| В пределах 0 - 1000°С | ||
| О2 |  = 0,9127 + 0,00012724 t = 0,9127 + 0,00012724 t
|  = 1,3046 + 0,00018183 t = 1,3046 + 0,00018183 t
|
 = 0,6527 + 0,00012724 t = 0,6527 + 0,00012724 t
|  = 0,9337 + 0,00018183 t = 0,9337 + 0,00018183 t
| |
| N2 |  = 1,0258 + 0,00008382 t = 1,0258 + 0,00008382 t
|  = 1,2833 + 0,00010492 t = 1,2833 + 0,00010492 t
|
 = 0,7289 + 0,00008382 t = 0,7289 + 0,00008382 t
|  = 0,9123 + 0,00010492 t = 0,9123 + 0,00010492 t
| |
| СО |  = 1,0304 + 0,00009575 t = 1,0304 + 0,00009575 t
|  = 1,2883 + 0,00011966 t = 1,2883 + 0,00011966 t
|
 = 0,7335 + 0,00009575 t = 0,7335 + 0,00009575 t
|  = 0,9173 + 0,00011966 t = 0,9173 + 0,00011966 t
| |
| Воздух |  = 0,9952 + 0,00009349 t = 0,9952 + 0,00009349 t
|  = 1,2870 + 0,00012191 t = 1,2870 + 0,00012191 t
|
 = 0,7084 + 0,00009349 t = 0,7084 + 0,00009349 t
|  = 0,9161 + 0,00012191 t = 0,9161 + 0,00012191 t
| |
| Н2О |  = 1,8401 + 0,00029278 t = 1,8401 + 0,00029278 t
|  = 1,4800 + 0,00023551 t = 1,4800 + 0,00023551 t
|
 = 1,3783 + 0,00029278 t = 1,3783 + 0,00029278 t
|  = 1,1091 + 0,00023551 t = 1,1091 + 0,00023551 t
| |
| SО2 |  = 0,6314 + 0,00015541 t = 0,6314 + 0,00015541 t
|  = 1,8472 + 0,00004547 t = 1,8472 + 0,00004547 t
|
 = 0,5016 + 0,00015541 t = 0,5016 + 0,00015541 t
|  = 1,4763 + 0,00004547 t = 1,4763 + 0,00004547 t
| |
| В пределах 0 - 1500°С | ||
| H2 |  = 1,42494 + 0,00059574 t = 1,42494 + 0,00059574 t
|  = 1,2803 + 0,00005355 t = 1,2803 + 0,00005355 t
|
 = 1,01241 + 0,00059574 t = 1,01241 + 0,00059574 t
|  = 0,9094 + 0,00005355 t = 0,9094 + 0,00005355 t
| |
| CO2 |  = 0,8725 + 0,00024053 t = 0,8725 + 0,00024053 t
|  = 1,7250 + 0,00004756 t = 1,7250 + 0,00004756 t
|
 = 0,6837 + 0,00024053 t = 0,6837 + 0,00024053 t
|  = 1,3540 + 0,00004756 t = 1,3540 + 0,00004756 t
|
Задачи
4.1. Найти объемную теплоемкость кислорода при постоянном объеме и постоянном давлении, считая с=const.
Решение:
По табл. 4.1 для двухатомных газов: mCv=20.93 кДж/(кмоль К);
mCp=29.31 кДж/(кмоль К);
Cледовательно, для кислорода (и любого двухатомного газа)
Сv=mCv/22.4=20.93/22.4=0.934 кДж/(м3 К);
Cp=mCp/22.4=29.31/22.4=1.308 кДж/(м3 К).
Ответ: Ср=1.308 кДж/(м3 К); Сv=0.934 кДж/(м3 К).
4.2. Определить значение массовой теплоемкости кислорода при постоянном объеме и постоянном давлении, считая с=const.
Ответ: Ср=0.916 кДж/(кг К); Сv=0.654 кДж/(кг К).
4.3. Вычислить среднюю массовую и среднюю объемную теплоемкость окиси углерода при постоянном объеме для интервала температур 0-1200 0С, если известно, что для окиси углерода (mСpm)01200=32.192 кДж/(кмоль К).
Решение:
На основании формул (4.1),(4.2) и (4.3) имеем
(mСv)01200=32.192-8.314=23.877 кДж/(кмоль К);
(Сvm)01200=(mCv)01200/28=23.877/28=0.8528 кДж/(кг К);
(Cvm)01200=(mCv)01200/22.4=23.877/22.4=1.0659 кДж/(м3 К).
Ответ: (mСv)01200=23.877 кДж/(кмоль К); (Сvm)01200 =0.8528 кДж/(кг К);
(Cvm)01200 =1.0659 кДж/(м3 К).
4.4. Вычислить среднюю теплоемкость Сpm для воздуха при постоянном давлении в пределах 200-800 0С, считая зависимость теплоемкости от температуры нелинейной.
Ответ: (Сpm)200800=1.091 кДж/(кг К).
4.5. Вычислить среднюю теплоемкость Сpm и Сvm в пределах 200-800 0С для СО, считая зависимость теплоемкости от температуры линейной.
Ответ: Сpm=1.1262 кДж/(кг К); Сvm=1.0371 кДж/(м3 К).
4.6. Найти среднюю теплоемкость Сpm и Cvm для воздуха в пределах 400-1200 0С, считая зависимость теплоемкости от температуры нелинейной.
Ответ: Сpm =1.4846 кДж/(м3 К);Cvm =1.1137кДж/(м3 К).
4.7. В закрытом сосуде объемом V=300 л находится воздух при давлении р1=0.8 МПа и температуре t1=20 0С. Какое количество теплоты необходимо подвести для того, чтобы температура воздуха поднялась до t2=120 0С? Задачу решить, принимая теплоемкость воздуха постоянной, а также учитывая зависимость теплоемкости от температуры. Определить относительную ошибку, получаемую в первом случае.
Ответ: Q=77.3 кДж. Относительная ошибка e»0.25 %.
4.8. Воздух охлаждается от 1000 0С до 100 0С в процессе с постоянным давлением. Какое количество теплоты теряет 1 кг воздуха? Задачу решить, принимая теплоемкость воздуха постоянной, а также учитывая зависимость теплоемкости от температуры. Определить относительную ошибку, получаемую в первом случае.
Ответ: 1). qcp=const =-911.9 кДж/кг;
2). qcp=f(t)=-990.1 кДж/кг; e»8%.
4.9. В сосуде объемом 300 л находится кислород при давлении р1=0.2 МПа и температуре t1=20 0С. Какое количество теплоты необходимо подвести, чтобы температура кислорода повысилась до t2=300 0С? Какое давление установится при этом в сосуде? Зависимость теплоемкости от температуры принять нелинейной.
Ответ: Qv= 152.8 кДж; Р2=0.39 МПа
4.10. Газовая смесь имеет следующий состав по объему: СО2=0.12; O2=0.07; N2=0.75; H2O=0.06.Определить среднюю массовую теплоемкость Сpm, если смесь нагревается от 100 0С до 300 0С.
Ответ: Сpm=1.0928 кДж/(кг К)