Основные газовые процессы. Изохорный процесс

Основными термодинамическими процессами являются:

1) процесс сообщения или отнятия теплоты при постоянном объеме газа (V=const) – изохорный процесс;

2) процесс сообщения или отнятия теплоты при постоянном давлении (P=const) – изобарный процесс;

3) процесс сообщения или отнятия теплоты при постоянной температуре (T=const) – изотермический процесс;

4) процесс без сообщения или отнятия теплоты извне (dq=0) - адиабатный процесс;

5) процесс, в котором изменение параметров подчиняется уравнению

,

где m - величина, постоянная для данного процесса, - политропный процесс.

В изохорном процессе зависимость между начальными и конечными параметрами определяется следующей зависимостью

(7.1)

Изменение внутренней энергии

(7.2)

Если в процессе участвует кг или м³ газа, то количество теплоты или изменение внутренней энергии газа

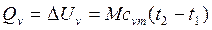(7.3)

Задачи

7.1. Газ при давлении Р₁=1МПа и температуре t₁=20 ^ОС нагревается при постоянном объеме до t₂=300 ^ОС. Найти конечное давление газа.

Ответ: Р₂=1.956 МПа.

7.2. В закрытом сосуде емкостью V=0.3 м³ содержится 2.75 кг воздуха при давлении Р₁=0.8 МПа и температуре t₁=25 ^ОС. Определить давление и удельный объем после охлаждения воздуха до 0 ^ОС.

Ответ: Р₂=0.732 МПа, v₂=0.109 м³/кг.

7.3. В закрытом сосуде заключен газ при разрежении Р₁=6667 Па и температуре t₁=70 ^ОС. Показание барометра - 101325 Па. До какой температуры нужно охладить газ, чтобы разрежение стало Р₂=13 332 Па?

Решение:

Так как процесс происходит при V =const, то согласно формуле (7.1)

(101 325-6667)/(101 325-13332)=(273+70)/T₂.

 

Отсюда

Т₂=87993*343/94658=318.8 K; t₂=45.8°С.

Ответ: t₂=45.8 °С

7.4. До какой температуры t₂ нужно нагреть газ при V=const, если начальное давление газа P₁=0.2 МПа и температура t₁=20 °С, а конечное давление P₂=0.5 МПа.

Ответ: До t₂=459.5 °С.

7.5. В закрытом сосуде емкостью V=0.6 м³ содержится воздух при давлении р₁=0.5 МПа и температуре t₁=20 °С. В результате охлаждения сосуда воздух, содержащийся в нем, теряет 105 кДж. Принимая теплоемкость воздуха постоянной, определить, какое давление и какая температура устанавливаются после этого в сосуде.

Решение:

Пользуясь уравнением состояния, находим массу воздуха в сосуде

M=РV/RT=0.5∙10⁶∙0.6/287∙293=3.57 кг.

Количество теплоты, отводимой от воздуха в процессе, определяется уравнением

Q=Mc_vm(t₂-t₁)

откуда

t₂=Q/Mc_vm+t₁= -105/3.57∙0.723+20= -40.7+20= -20.7 °С.

Значение с_vm=0.723 получено из выражения c_vm=mc_vm/m=20.93/28.96 (для двухатомных газов).

Из соотношения параметров в изохорном процессе имеем

Р₂=Р₁∙Т₂/Т₁=0.5∙(273-20.7)/293=0.43 МПа.

Ответ: Р₂=0.43 МПа

7.6. В закрытом сосуде емкостью V=0.5 м³ содержится двуокись углерода при р₁=0.6 МПа и температуре t₁=527 °С. Как изменится давление газа, если от него отнять 420 кДж? Принять зависимость С=f(t) линейной.

Ответ: р₂=0.42 МПа.

7.7. Сосуд емкостью 90 л содержит воздух при давлении 0.8 МПа и температуре 30 °С. Определить количество теплоты, которое необходимо сообщить воздуху, чтобы повысить его давление при V=const до 1.6 МПа. Принять зависимость с=f(t) нелинейной.

Решение:

Из соотношения параметров изохорного процесса получим

Т₂=Т₁∙P₂/P₁=303∙1.6/0.8=606 К, t₂=606-273=333°С.

По уравнению q_v=c_vm2t₂-c_vm1t₁.

Пользуясь табл. 4.2,4.3, находим

с_vm1=0.7173 кДж/кг К; c_vm2=0.7351 кДж/кг К..

Следовательно,

q_v=0.7351∙333-0.7173∙30=223.2 кДж/кг.

Массу воздуха, находящегося в резервуаре, определяем из уравнения

M=p₁V₁/RT₁=0.8∙106∙0.09/287∙303=0.8278 кг,

а сообщенное ему количество теплоты

Q_v=0.8278∙223.2=184.8 кДж.

7.8. До какой температуры нужно охладить 0.8 м³ воздуха с начальным давлением 0.3 МПа и температурой 15°С, чтобы давление при постоянном объеме понизилось до 0.1 МПа? Какое количество теплоты нужно для этого отвести? Теплоемкость воздуха принять постоянной.

Отв. До t₂= -177°С; Q=- 402 кДж.

Изобарный процесс

Процесс сообщения или отнятия теплоты при постоянном давлении называется изобарным (P=const)

Зависимость между начальными и конечными параметрами процесса

(8.1)

Работа 1 кг газа

(8.2)

или

. (8.3)

Для М кг газа

(8.4)

или

. (8.5)

Если в процессе участвует М кг или V_н м³ газа, то количество теплоты

(8.6)

 

Задачи

8.1. Какое количество теплоты необходимо затратить, чтобы нагреть 2 м³ воздуха при постоянном избыточном давлении р=0.2 МПа от t₁=100°С до t₂=500°С? Какую работу при этом совершит воздух?

Давление атмосферы принять равным 101 325 Па.

Решение:

Согласно уравнению

q_p=c_pm2t₂-c_pm1t₁.

c_pm1=1.0061 кДж/кг К; c_pm2=1.0387 кДж/кг К.

Следовательно,

q_p=1.0387∙500-1.0061∙100=418.7 кДж/кг.

Массу воздуха определяем из характеристического уравнения

M=РV/RT=(0.2+0.1013)10⁶∙2/287∙373=5.63 кг.

Таким образом,

Q_p=Mq_p=5.63∙418.7=2357 кДж.

Количество теплоты можно получить не только по массе воздуха, но и по его объему. В этом случае уравнение следует написать так:

q_p=с’_pm2t₂-c’_pm1t₁.

Пользуясь табл. 4.2, получаем

c’_pm1=(c’_pm)₀¹⁰⁰=1.3004 кДж/м³ К;

c’_pm2=(c’_pm)₀⁵⁰⁰=1.3427 кДж/м³ К.

Тогда

q_p=1.3427∙500-1.3004∙100=541.4 кДж/м³.

Объем воздуха должен быть приведен к нормальным условиям. Согласно уравнению

V_н=pVT_н/Tp_н=0.3013∙2∙273/373∙0.1013=4.35 м².

Таким образом,

Q_p=q_pV_н=541.4∙4.35=2356 кДж.

Работа газа по уравнению

L=MR(t₂-t₁)=5.63∙287∙400=646.3 кДж.

8.2. Определить количество теплоты, необходимое для нагревания 2000 м³ воздуха при постоянном давлении р=0.5 МПа от t₁=150°С до t₂=600°С. Зависимость теплоемкости от температуры считать нелинейной.

Ответ: Q_р=3937 МДж.

8.3. В установке воздушного отопления внешний воздух при t₁=-15°С нагревается в калорифере при р=const до 60°С. Какое количество теплоты надо затратить для нагревания 1000 м³ наружного воздуха? Теплоемкость воздуха считать постоянной. Давление воздуха принять равным 101 325 Па.

Отв. 103 МДж.

8.4. В цилиндре находится воздух при давлении р=0.5 МПа и температуре t₁=400°С. От воздуха отнимается теплота при постоянном давлении таким образом, что в конце процесса устанавливается температура t₂=0°С. Объем цилиндра, в котором находится воздух, равен 400 л.

Определить количество отнятой теплоты, конечный объем, изменение внутренней энергии и совершенную работу сжатия. Зависимость теплоемкости от температуры считать нелинейной.

 

Решение:

Количество отнятой теплоты по формуле

Q_p=V_нc”_pm(t_2-t1).

Объем воздуха при нормальных условиях определим из выражения

V_н=pVT_н/p_нT=0.5∙0.4∙273/0.1013∙673=0.8 м³.

По табл. 4.2, 4.3 находим

c’_pm=1.3289 кДж/м³ К.

Следовательно,

Q_p=0.8∙1.3289(0-400)=- 425кДж.

Это же количество теплоты можно вычислить не только по объему воздуха, но и по его массе:

Q_p=Mc_pm(t₂-t₁).

Массу воздуха определяем из характеристического уравнения

M=Р₁V₁/RT₁=0.5∙10⁶∙0.4/287∙673=1.035 кг.

Из табл. 4.2 находим

c_pm=1.0283 кДж/кг К.

Следовательно,

Q_p=1.035∙1.0283(0-400)=-425 кДж.

Конечный объем получим из уравнения (10.4)

V₂=V₁T₂/T₁=0.4∙273/673=0.1622 м³.

Изменение внутренней энергии

DU=V_нc’_vm(t₂-t₁).

Пользуясь табл. 4.2, находим

c’_vm=0.9579 кДж/м³ К.

Следовательно,

DU=0.8∙0.9579(0-400)=-306.5 кДж.

Работа, затраченная на сжатие, по формуле (8.4)

L=Р(V₂-V₁)=0.5∙10⁶(0.1622-0.4)=-118.9 кДж.

8. 5. Для использования отходящих газов двигателя мощностью N=2500 кВт установлен подогреватель, через который проходит 60000 м³/ч воздуха при температуре t₁=15 °С и давлении Р=0.101 МПа. Температура воздуха после подогревателя равна 75 °С.

Определить, какая часть теплоты топлива использована в подогревателе? К.П.Д. двигателя принять равным 0.33. Зависимость теплоемкости от температуры считать линейной.

Ответ: 17.4%.

8.6. 2 м³ воздуха с начальной температурой t₁=15 °С расширяются при постоянном давлении до 3 м³ вследствие сообщения газу 837 кДж теплоты. Определить конечную температуру, давление газа в процессе и работу расширения.

Ответ: t₂=159°С, Р=0.24 МПа, L=239 кДж.

8.7. Отходящие газы котельной установки проходят через воздухоподогреватель. Начальная температура газов t_г1=300 °С, конечная t_г2=160 °С; расход газов равен 1000 кг/ч. Начальная температура воздуха составляет t_в1=15 °С, а расход его равен 910 кг/ч.

Определить температуру нагретого воздуха t_в2, если потери воздухоподогревателя составляют 4 %. Средние теплоемкости (c_pm) для отходящих из котла газов и воздуха принять соответственно равными 1,0467 и 1,0048 кДж/кг К.

Ответ: t_в2=168,9 °С.

8.8. Определить, какая часть теплоты, подводимой к газу в изобарном процессе, расходуется на работу и какая - на изменение внутренней энергии.

Решение:

Аналитическое выражение первого закона термодинамики

dq=du+dl

может быть представлено в виде

du/dq+dl/dq=1.

Величина

dl/dq=1-du/dq

определяет ту долю от всей подводимой к газу теплоты, которая превращается в работу расширения. Так как для идеального газа в процессе Р=const

du=c_vdt и dq=c_pdt,

то

dl/dq=1-c_vdt/c_pdt.

Принимая к=1.4, получаем

dl/dq=1-1/1.4=0.285.

Следовательно, в изобарном процессе только 28.5% теплоты, подводимой к газу, превращается в работу. Вся остальная теплота, т.е. 71.5%, расходуется на увеличение внутренней энергии.

Изотермический процесс

Процесс сообщения или отнятия теплоты при постоянной температуре называется изотермическим.

Уравнение процесса (9.1)

Зависимость между начальными и конечными параметрами в изотермическом процессе определяется формулами:

(9.2)

Работу 1 кг идеального газа находят их уравнений:

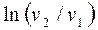; (9.3)

; (9.4)

; (9.5)

. (9.6)

Если в процессе участвует М кг газа, то полученные из формул 9.3 – 9.6 значения нужно увеличить в М раз. Можно также для этого случая в формулах 9.5 и 9.6 заменить удельный объем полным объемом . Тогда получим

; (9.7)

. (9.8)

Так как в изотермическом процессе , то для идеального газа изменение внутренней энергии равно

.

Количество теплоты, сообщаемой газу или отнимаемой от него

(9.9)

или для М кг газа

(9.10)

 

Задачи

9.1. 1 кг воздуха при температуре t₁=30°С и начальном давлении р₁=0.1 МПа сжимается изотермически до конечного давления р₂=1 МПа.

Определить конечный объем, затрачиваемую работу и количество теплоты, отводимой от газа.

Решение:

Найдем начальный объем воздуха из уравнения состояния:

v₁=RT₁/p₁=287∙303/0.1∙10⁶=0.87 м³/кг.

Так как в изотермическом процессе p₁v₁=p₂v₂ то конечный объем

v₂=v₁∙p₁/p₂=0.87∙1/10=0.087 м³/кг.

Работа, затрачиваемая на сжатие 1 кг воздуха, получается из уравнения (9.8):

L=RTlnp₁/p₂=2.303RTlnp₁/p₂=-2.303∙287∙303lg10=-200 кДж/кг.

Количество теплоты, отводимой от газа, равно работе, затраченной на сжатие.

Следовательно,

q=-200кДж/кг.

9.2. Воздух в количестве 0.5 кг при р₁=0.5 МПа и t₁=30°С расширяется изотермически до пятикратного объема.

Определить работу, совершаемую газом, конечное давление и количество теплоты, сообщаемой газу.

Ответ: р₂=0.1 МПа, L=Q=70 кДж.

9.3. Для осуществления изотермического сжатия 0.8 кг воздуха при р₁=0.1 МПа и t=25°С затрачена работа в 100 кДж.

Найти давление р₂ сжатого воздуха и количество теплоты, которое необходимо при этом отвести от газа?

Ответ: р₂=0.322 МПа, Q=-90 кДж.

9.4. 8 м³ воздуха при р₁=0.09 МПа и t₁=20°С сжимаются при постоянной температуре до 0.81 МПа.

Определить конечный объем, затраченную работу и количество теплоты, которое необходимо отвести от газа.

Ответ: V₂=0.889 м3, L=Q=-1581 кДж.

9.5. При изотермическом сжатии 0.3 м³ воздуха с начальными параметрами р₁=1 МПа и t₁=300°С отводится 500 кДж теплоты.

Определить конечный объем V₂ и конечное давление р₂.

Ответ: V₂=0.057 м³, р₂=5.26 МПа.

9.6. 10 кг воздуха при давлении р₁=0.12 МПа и температуре t₁=30°С сжимаются изотермически; при этом в результате сжатия объем увеличивается в 2.5 раза.

Определить начальные и конечные параметры, количество теплоты, работу и изменение внутренней энергии.

Ответ: V₁=7.25 м³; V₂=2.9 м³; p₂=0.3 МПа; Q=L=-797 кДж; DU=0.

Адиабатный процесс

,

где k=c_p/c_v - показатель адиабаты.

Зависимости между начальными и конечными параметрами процесса:

Между p и v: , (10.1)

между T и v: , (10.2)

между p и T: . (10.3)

 

Работу 1 кг газа находят по следующим формулам:

; (10.4)

; (10.5)

; (10.6)

. (10.7)

Для определения работы кг газа нужно в формулах (9.4), (9.5) и (9.7) заменить удельный объем v общим объемом V газа.

Тогда получим

(10.8)

; (10.9)

. (10.10)

Формула (9.6) для M кг газа примет следующий вид:

;

Уравнение первого закона для адиабатного процесса имеет вид:

, (10.12)

следовательно, или , т.е. изменение внутренней энергии газа и работа адиабатного процесса равны по величине и противоположны по знаку.

Изменение внутренней энергии идеального газа в адиабатном процессе может быть также выражено уравнением:

. (10.13)

Задачи

10.1. 1 кг воздуха при начальной температуре t₁=30 °С и давлении Р₁=0.1 МПа сжимается адиабатно до конечного давления Р₂=1 МПа.

Определить конечный объем, конечную температуру и затрачиваемую работу.

Решение:

Из соотношения параметров в адиабатном процессе находим

по уравнению

T₂/T₁=(Р₂/Р₁)^k-1/k,

откуда

T₂=T₁(Р₂/Р₁)^k-1/k.

Принимая к=1.4, получаем

Т₂=303∙10^0.4/1.4=303∙10^0.286=303N;

lgN=lg 10^0.286=0.286lg10=0.286;

M=1.931;

T₂=303∙1.931=585 K; t₂=312°С.

Значение величины (Р₂ /Р₁)^к-1/к для адиабатного сжатия при р₂/p₁=10 величина (Р₂/Р₁)^к-1/к=1.931.

Затраченная работа по уравнению (9.6)

L=R∙ (T₁-T₂)/(k-1)=0.287∙(303-585)/0.4=-202 кДж/кг.

Конечный объем определяется из уравнения состояния

v₂=RT₂/Р₂=287∙585/1∙10⁶=0.168 м³/кг.

10.2. 1 кг воздуха при температуре t₁=15°С и начальном давлении Р₁=0.1 МПа адиабатно сжимается до 0.8 МПа.

Найти работу, конечный объем и конечную температуру.

Ответ: t₂=248°С; v₂=0.187 м³/кг; L=-167.2 кДж/кг.

10.3. Воздух при давлении Р₁=0.45 МПа, расширяясь адиабатно до 0.12 МПа, охлаждается до t₂=-45 °С.

Определить начальную температуру и работу, совершенную 1 кг воздуха.

Ответ: t₁=61°С; L=75.3 кДж/кг.

10.4. 1 кг воздуха, занимающий объем v₁=0.0887 м³/кг при Р₁=1 МПа, расширяется до 10-кратного объема.

Получить конечное давление и работу, совершенную воздухом, в изотермическом и адиабатном процессах.

Ответ: 1). Т=const; Р₂=0.1МПа; L=204 кДж/кг; 2). dQ=0; p₂=0.04 МПа; L=133.5 кДж/кг.

10.5. Воздух при температуре t₁=25 °С адиабатно охлаждается до t₂=-55 °С; давление при этом падает до 0.1 МПа.

Определить начальное давление и работу расширения 1 кг воздуха.

Ответ: Р₁=0.3 МПа; L=57.4 кДж/кг.

10.6. Адиабатным сжатием повысили температуру воздуха в двигателе так, что она стала равной температуре воспламенения нефти, объем при этом уменьшился в 14 раз.

Определить конечную температуру и конечное давление воздуха, если Р₁=0.1 МПа и t₁=100 °С.

Решение:

Конечную температуру определяем по формуле:

T₂=T₁(v₁/v₂)^k-1=373∙14^0.4=373∙2.86=1067 K.

Конечное давление находим из уравнения (91)

Р₂=Р₁(T₂/T₁)^k/k-1=0.1(1067/373)^1.4/0.4=0.1∙2.86^3.5=4 МПа.

10.7. Работа, затраченная на адиабатное сжатие 3 кг воздуха, составляет 471 кДж. Начальное состояние воздуха характеризуется параметрами: t₁=15 °С; Р₁=0.1 МПа.

Определить конечную температуру и изменение внутренней энергии.

Ответ: t₂=234 °С; DU=-471 кДж.

10.8. 1 м³ воздуха при давлении 0,095 МПа и начальной температуре 10°С сжимается по адиабате до 0,38 МПа.

Определить температуру и объем воздуха в конце сжатия и работу, затраченную на сжатие.

Ответ: t₂=148 °С, V₂=0.373 м³, L=-117 кДж.

10.9. 1 кг воздуха при температуре t₁=17°С сжимается адиабатно до объема, составляющего 1/5 начального, а затем расширяется изотермически до первоначального объема.

Определить работу, произведенную воздухом в результате обоих процессов.

Ответ: L= 67 кДж/кг.

 

Политропный процесс

Уравнение политропы в системе координат при постоянной теплоемкости

,

где - показатель политропы.

Характеристикой политропного процесса является величина

, (11.1)

которая может быть определена из выражения

, (11.2)

где .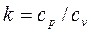

Зависимости между начальными и конечными параметрами процесса:

между и , (11.3)

между и 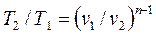, (11.4)

между 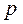и . (11.5)

Работу 1 кг газа находят по следующим формулам:

; (11.6)

; (11.7)

; (11.8)

. (11.9)

Если количество теплоты, участвующей в процессе, известно, то работа может быть также вычислена по формуле

. (11.10)

Для определения работы M кг газа нужно в формулах (11.6) – (11.8)заменить удельный объем v полным объемом V газа. Тогда получим

; (11.11)

; (11.12)

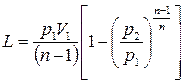; (11.13)

Формулы (11.9) и (11.10) для M кг газа имеют следующий вид:

; (11.14)

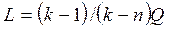. (11.15)

Теплоемкость политропного процесса можно найти из уравнения ,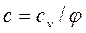

или, заменяя его значением из уравнения (11.2), получим

.

Количество теплоты, сообщаемой газу или отнимаемой от него:

(11.16)

(11.17)

Величину можно также определить из формулы (11.15), если известна работа политропного процесса:

. (11.18)

Изменение внутренней энергии газа в политропном процессе

. (11.19)

Показатель политропного процесса определяется из уравнения

. (11.20)

Задачи

11.1. 1 кг воздуха при р₁=0.5 МПа и t₁=111°С расширяется политропно до давления Р₂=0.1 МПа.

Определить конечное состояние воздуха, изменение внутренней энергии, количество подведенной теплоты и полученную работу, если показатель политропы n=1.2.

Решение:

Определяем начальный объем воздуха

v₁=RT₁/Р₁=(287∙384)/(0.5∙10⁶)=0.22 м³/кг.

Конечный объем воздуха находим из уравнения (11.3)

v₂=v₁(Р₁/Р₂)^1/n=0.22∙5^1/1.2=0.84 м³/кг.

Конечную температуру проще всего получить из характеристического уравнения

T₂=Р₂v₂/R=0.1∙10⁶∙0.84/287=293 K.

Величину работы находим из уравнения (10.9)

L=R(T₁-T₂)/(n-1)=287(384-293)/0.2=130 600 Дж/кг=130.6 кДж/кг.

Изменение внутренней энергии

Du=c_v(T₂-T₁)=20.93(293-384)/28.96=-65.8 кДж/кг.

Количество теплоты, сообщенной воздуху, по уравнению (11.17)

q=c_v(n - k)/(n - 1)·(t₂-t₁)=0.72(1.2-1.4)/(1.2-1) (20-111)=65.8 кДж/кг.

Нетрудно видеть, что в этом процессе внешняя работа совершается за счет подведенной теплоты и уменьшения внутренней энергии. Исходя из этого можно проверить полученные результаты следующим образом:

q=Du+L; L=q - Du=65.8-(-65.8)=131.6 кДж/кг.

Этот же результат получен выше другим путем.

11.2. 1.5 кг воздуха сжимают политропно от р₁=0.09 МПа и t₁=18°С до р₂=1 МПа, температура при этом повышается до t₂=125°С.

Определить показатель политропы, конечный объем, затраченную работу и количество отведенной теплоты.

Решение:

По формуле

(n-1)/n=(lgT₂/T₁)/(lgp₂/p₁)=(lg398/291)/(lg100/9)=0.13,

отсюда

n=1/(1-0.13)=1.149.

Конечный объем находим из характеристического уравнения

V₂=MRT₂/p₂=1.5∙287∙398/10⁶=0.171 м³.

Затраченная работа по уравнению (10.46)

L=MR(t₁-t₂)/(n-1)=1.5∙287(18-125)/0.149=-309200 Дж=-309.2 кДж.

Количество отведенной теплоты по уравнению

Q=Mc_v(n-k)/(n-1) (t₂-t₁)=

=1.5∙20.93/28.96∙(1.149-1.4)/(1.149-1) (125-18)=-195.4 кДж.

11.3. Воздух в количестве 3 м³ расширяется политропно от р₁=0.54 МПа и t₁=45°С до р₂=0.15 МПа. Объем, занимаемый при этом воздухом, становится равным 10 м³.

Найти показатель политропы, конечную температуру, полученную работу и количество подведенной теплоты.

Ответ: m=1.064, t₂=21.4°С, L=1875 кДж, Q=1575 кДж.

11.4. В цилиндре двигателя с изобарным подводом теплоты сжимается воздух по политропе с показателем m=1.33.

Определить температуру и давление воздуха в конце сжатия, если степень сжатия (e=V₁/V₂) равна 14, t₁=77°С и р₁=0.1 МПа.

Ответ: t₂=564°С, р₂=3.39 МПа.

Знак плюс(+) показывает, что теплота в данном процессе подводится. Об этом можно судить также по величине показателя политропы.

Изменение внутренней энергии

DU= Q – L =672.4-1923=-1250.6 кДж.

Знак минус (-) показывает, что внутренняя энергия убывает. В данном процессе работа совершается за счет подводимой извне теплоты, а также внутренней энергии газа.

11.5. В процессе политропного сжатия затрачивается работа, равная 195 кДж, причем в одном случае от газа отводится 250 кДж, а в другом - газу сообщается 42 кДж.

Определить показатели обеих политроп.

Ответ: 1). m=0.9, 2). m=1.49.

11.6. 1.5 м³ воздуха сжимаются от 0.1 МПа и 17°С до 0.7 МПа, конечная температура при этом равна 100°С.

Какое количество теплоты требуется отвести, какую работу затратить и каков показатель политропы?

Ответ: Q=-183 кДж, L=-290 кДж, m=1.147.

11.7. 0.01 м³ воздуха при давлении р₁=1 МПа и температуре t₁=25°С расширяется в цилиндре с подвижным поршнем до 0.1 МПа.

Найти конечный объем, конечную температуру, работу, произведенную газом, и подведенную теплоту, если расширение в цилиндре происходит: а)изотермически, б)адиабатно и в)политропно с показателями m =1.3.

Решение:

а). Изотермическое расширение. Конечный объем определяют по формуле (11.11)

V₂=V₁p₁/p₂=0.01∙1/0.1=0.1 м³.

Так как в изотермическом процессе t=const, то конечная температура t₂=t₁=25°С.

Работа газа по уравнению (10.17)

L=p₁V₁lnp₁/p₂=1∙10⁶∙0.01∙2.303lg10=23 000 Дж.

Количество подведенной теплоты по формуле (11.19)

Q=L=23 кДж.

б). Адиабатное расширение. Конечный объем определяется по уравнению (11.20)

V₂=V₁(p₁/p₂)^1/k=0.01∙10^1/1.4.

Пользуясь табл. XIX, получаем 10^1/1.4=5.188.

Следовательно

V₂=0.01∙5.188=0.05188 м³.

Конечная температура воздуха на основании уравнения (11.22)

T₂=T₁(p₂/p₁)^k-1/k=298(0.1/1)^1.4-1/1.4=154.3 K; t₂=-118.7°С.

Работа газа по уравнению (10.29)

L=p₁V₁/(k-1) (1-(p₂/p₁)^k-1/k)=1∙10⁶∙0.01/0.4∙(1-1/1.931)=

=25000∙0.48=12 000Дж=12 кДж.

в). Политропное расширение. Конечный объем найдем из уравнения (11.35)

V₂=V₁(p₁/p₂)^1/m=0.01∙10^1/1.3=0.01∙5.885=0.05885 м³.

Конечная температура по уравнению (10.37)

T₂=T₁(p₁/p₂)^m-1/m=298(0.1/1)^0.3/1.3=175.2 K; t₂=-97.8 °С.

Работа газа по уравнению (10.45)

L=p₁V₁/(m-1) (1-(p₂/p₁)^m-1/m)=

=1∙10⁶∙0.01/0.3∙(1-(0.1/1)^0.3/1.3)=13700 Дж=13.7 кДж.

Подведенная теплота по уравнению (10.50)

Q=L(k-m)/(k-1)=13.7∙0.1/0.4=3.425 кДж.

11.8. В процессе политропного расширения воздуху сообщается 83.7 кДж тепла.

Найти изменение внутренней энергии воздуха и произведенную работу, если объем воздуха увеличился в 10 раз, а давление его уменьшилось в 8 раз.

Ответ: DU=16.7 кДж; L=6702 кДж.

11.10. Воздух расширяется по политропе, совершая при этом работу, равную 270 кДж, причем в одном случае ему сообщается 420 кДж теплоты, а в другом - от воздуха отводится 92 кДж теплоты.

Определить в обоих случаях показатели политропы.

Ответ: 1). m=0.78; 2). m=1.88.

11.11. 2 м³ воздуха при давлении р₁=0.09 МПа и температуре t₁=40°С сжимаются до давления р₂=1.1 МПа и объема V₂=0.5 м³.

Определить показатель политропы, работу сжатия и количество отведенной теплоты.

Ответ: m=1.23; L=-652 кДж; Q=-272 кДж.