Второй закон термодинамики определяет направление, в котором протекают процессы, устанавливает условия преобразования тепловой энергии в механическую, а также определяет максимальное значение работы, которая может быть произведена тепловым двигателем.
Математически он может быть выражен следующим образом:
, (13.1)
где 
- бесконечно малое приращение энтропии системы;
- бесконечно малое количество теплоты, полученной системой от источника теплоты;
- абсолютная температура источника теплоты.
Аналитическое выражение второго закона термодинамики для бесконечно малого обратимого процесса имеет вид
dQ=TdS, (13.2)
а так как, согласно первому закону термодинамики
dQ= dU+PdV
то уравнение (13.2) примет вид
TdS = dU+PdV
Основным уравнением для определения энтропии в обратимом процессе является выражение
ds=dq/T (13.3)
Определение энтропии для любого состояния газа, отсчитанной от нормального состояния производят по следующим формулам.
При переменной теплоемкости, исходя из линейной зависимости ее от температуры:
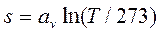
; (13.4)
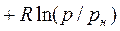
; (13.5)
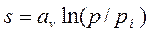
. (13.6)
При постоянной теплоемкости
; (13.7)
; (13.8)
(13.9)
Изменение энтропии между двумя произвольными состояниями газа 1 и 2 определяют по следующим формулам.
При переменной теплоемкости, считая зависимость ее от температуры линейной:
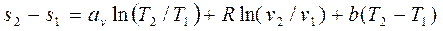; (13.10)
; (13.11)
(13.12)
При постоянной теплоемкости 
; (13.13)
; (13.14)
. (13.15)
Если работа совершается с помощью газа, параметры которого отличаются от параметров окружающей среды, то максимальная работа, которую может произвести этот газ, достижима лишь при условии его перехода от начального состояния к состоянию среды обратимым путем.
При этом максимальная полезная работа меньше максимальной работы на величину работы вытеснения воздуха окружающей среды.
Величина максимальной полезной работы определяется формулой
. (13.16)
В этой формуле параметры, имеющие индекс 1 и 2, относятся соответственно к начальному и конечному состоянию источника работы, а параметры с индексом 0 относятся к рабочей среде.
Так как выражения 
и 
представляют собой соответственно абсолютную величину работы адиабатного и изотермического процесса, то формулу (6.16) можно представить в виде:
. (13.17)
Задачи
13.1. Определить энтропию 1 кг кислорода при р=0.8 МПа и t=250°С. Теплоемкость считать постоянной.
Решение:
По формуле (13.8)
s=Cpln(T/273)-R ln(p/pн).
Так как для двухатомных газов mСр=29.3 кДж/(кмоль К), а R=8.314 кДж/(кмоль К), то
s=29.3/32∙2.303∙lg(523/273)-8.314/32∙2.303∙lg(8/1.013);
s=0.5978-0.5373=0.0605 кДж/(кг К).
13.2. Найти энтропию 1 кг кислорода при р=0.8 МПа и t=250°С. Теплоемкость считать переменной, приняв зависимость ее от температуры линейной.
Решение:
По формуле (13.5)
s=apln(T/273)-Rln(p/pн)+b(T-273).
Из табл. 5 для кислорода
Сpm=0.0127+0.00012724t кДж/(кг К).
Поэтому формула линейной зависимости истинной теплоемкости будет иметь вид
Ср=0.9127+0.00025448t кДж/(кг К),
или
Ср=0.8432+0.00025448Т кДж/(кг К).
Таким образом,
а=0.8432; b=0.00025448;
значение энтропии
s=0.8432∙2.303∙lg(523/273)-8.314/32∙lg(0.8/0.1013)+0.00025448∙(523-273);
s=0.5476-0.5371+0.0634=0.0739 кДж/(кг К).
Для тех же условий, но при постоянной теплоемкости (см. 1) значение энтропии s=0.0605 кДж/(кг К), т.е. меньше на
(0.0739-0.0605)/0.0739=0.0134/0.0739=18.1%.
Этот результат показывает, что для повышенных и высоких температур следует пользоваться зависимостью c=f(t).
13.3. 1 кг воздуха сжимается по адиабате так, что объем его уменьшается в 6 раз, а затем при v=const давление повышается в 1.5 раза.
Найти общее изменение энтропии воздуха. Теплоемкость считать постоянной.
Решение:
Изменение энтропии воздуха в адиабатном процессе будет равно нулю.
Изменение энтропии в изохорном процессе определится по формуле (13.13):
Dsv=CvlnT3/T2=Cvlnp3/p2=Cvln1.5=2.303∙20.93/28.96lg1.5=0.293 кДж/(кг К);
следовательно,
Ds=Dsv=0.293 кДж/(кг К).
13.4. 1 кг воздуха сжимается от р1=0.1 МПа и t1=15°С до р2=0.5 МПа и t2=100°С.
Определить изменение энтропии. Теплоемкость считать постоянной.
13.5. 10 м3 воздуха, находящегося в начальном состоянии при нормальных условиях, сжимают до конечной температуры 400°С. Сжатие производится:1). изохорно, 2). изобарно, 3). адиабатно и 4). политропно с показателем политропы m=2.2.
Считая значение энтропии при нормальных условиях равным нулю и принимая теплоемкость воздуха постоянной, найти энтропию воздуха в конце каждого процесса.
Решение:
Находим массу 10 м3 воздуха при нормальных условиях:
M=pV/RT=0.1013∙106∙10/287∙273=12.9 кг.
Определяем изменение энтропии в каждом из перечисленных процессов:
1). изохорное сжатие
Ds1=s1=McvlnT/273=12.9 0.723 2.303lg673/273=8.42 кДж/К;
2). изобарное сжатие
Ds2=s2=McplnT/273=12.9 1.0117 2.303lg673/273=11.7 кДж/К;
3). адиабатное сжатие
Ds3=s3=0;
4).политропное сжатие
Ds4=s4=Mcv(m-k)/(m-1)lnT/273=
=12.9 0.723(2.2-1.4)/(2.2-1) 2.303lg673/273=5.61 кДж/К.
13.6. Найти приращение энтропии 3 кг воздуха) при нагревании его по изобаре от 0 до 400°С; б) при нагревании его по изохоре от 0 до 880°С; в) при изотермическом расширении с увеличением объема в 16 раз. Теплоемкость считать постоянной.
Ответ: а) Dsp=2.74; б) Dsv=3.13; в) Dst=2.36 кДж/К.
13.7. 1 кг воздуха сжимается по политропе от 0.1 МПа и 20°С до 0.8 МПа при m=1.2. Определить конечную температуру, изменение энтропии, количество отведенной теплоты и затраченную работу.
Ответ: t2=141°С; Ds=-0.2445 кДж/кг К; q=-87.1 кДж/кг; l=-173 кДж/кг.
13.8. В процессе политропного расширения воздуха температура его уменьшилась от t1=25°С до t2=-37°С. Начальное давление воздуха р1=0.4 МПа, количество его М=2 кг. Определить изменение энтропии в этом процессе, если известно, что количество подведенной к воздуху теплоты составляет 89.2 кДж.
Решение:
Количество теплоты, сообщаемое газу в политропном процессе составляет:
Q=Mcv(m-k)/(m-1) (t2-t1).
Подставляя значения известных величин, получаем
(m-k)/(m-1)=-89.2/(2 0.723 62)=-0.995.
Отсюда показатель политропы m=1.2.
Из соотношения параметров политропного процесса определяем конечное давление:
p2/p1=(T2/T1)m/(m-1); p2=p1(T2/T1)m/(m-1)=4(236/298)6=0.1 МПа.
Изменение энтропии по уравнению
Ds=M(cplnT2/T1-Rlnp2/p1);
следовательно,
Ds=2·2.3(29.3/28.96∙lg236/298-287/1000∙lg0.1/0.4)=
=4.6(-0.1026+0.1728)=0.323 кДж/К.
13.9. В сосуде объемом 400 л заключен воздух при давлении р1=0.1 МПа и температуре t1=-40°С. Параметры Среды р0=0.1 МПа и t0=20°С.Определить максимальную полезную работу, которую может произвести воздух, заключенный в сосуде. Представить процесс в диаграммах pv и Ts.
Ответ: Lmax(полезн) =4600 Дж.
Влажный воздух
В воздухе содержится то или иное количество влаги в виде водяного пара. Такую смесь сухого воздуха с водяным паром называют влажным воздухом.
С достаточной точностью можно применять к влажному пару все формулы, полученные для идеальных газов. Поэтому в дальнейшем принимаем, что влажный воздух подчиняется уравнению состояния идеальных газов:
pV=MRT,
А также закону Дальтона:
р=рв+рп, (14.1)
где р - давление влажного воздуха;
рв - парциальное давление сухого воздуха;
рп - парциальное давление пара.
Абсолютной влажностью воздуха называют массу водяного пара, содержащегося в 1 м3 влажного воздуха, или (что то же) плотность пара ρп при его парциальном давлении и температуре воздуха.
Величину
φ=ρп/ρmax, (14.2)
представляющую отношение абсолютной влажности воздуха приданной температуре ρп к его максимально возможной абсолютной влажности ρmax при той же температуре, называют относительной влажностью.
Относительная влажность может быть также приближенно найдена из уравнения:
φ=рп/рн, (14.3)
где рн - давление насыщения водяного пара при температуре смеси (по таблицам насыщенного пара).
Для характеристики влажного воздуха пользуются также понятием влагосодержание, под которым понимают отношение массы влаги (пара) во влажном воздухе к массе сухого воздуха в нем:
d=Мп/Мв=ρп/ρв, (14.4)
Величину d обычно измеряют в г/кг.
Выражение можно привести к следующему виду:
d=622(рп/(р-рп)) г/кг. (14.5)
Из этого уравнения следует, что
рп=р(d/(622+d)). (14.6)
Парциальное давление водяного пара при данном давлении влажного воздуха является функцией только влагосодержания, и наоборот. Поэтому аналогично уравнениям (14.5) и (14.6) можно написать:
d=622(рп/(р-рн)); (14.7)
рн=р(dmax/(622+dmax). (14.8)
где dmax - максимально возможное влагосодержание влажного воздуха (если температура его ниже температуры насыщения водяного пара при давлении смеси).
Отношение влагосодержания к максимально возможному влагосодержанию влажного воздуха (при той же температуре и давлении смеси) называют степенью насыщения и обозначают через:
Ψ=d/dmax. (14.9)
Из уравнений получаем зависимость между φ и Ψ:
φ=Ψ(622+dmax)/(622+d). (14.10)
Та температура, до которой надо охладить при постоянном давлении влажный воздух, чтобы он стал насыщенным (φ=100%), называют точкой росы tр.
Плотность влажного воздуха определяется из уравнения6
ρ=(р/287Т)-0,0129(φрн/Т), кг/м3 (14.11)
где рн и р выражены в Па, а Т - в К.
Энтальпию I влажного воздуха определяем как сумму энтальпий сухого воздуха и водяного пара. Энтальпию влажного воздуха относят к 1 кг сухого воздуха, т. е. к (1+d) кг влажного воздуха. Поэтому:
I=iв+iпd, (14.12)
или
I=iв+(iпd)/1000, (14.13)
если d берем в г/кг.
Энтальпия влажного воздуха:
I=t+0,001(2500+1,93t) кДж/кг. (14.14)
Истинная температура мокрого термометра определяется из формулы:
tм=t,м 
, (14.15)
где t,м - показания мокрого термометра,
tс - t,м - психрометрическая разность;
х - поправка к показанию мокрого термометра в прцентах.
Задачи.
14.1. Определить абсолютную влажность воздуха,если парциальное давление пара в нем рп=0.014 МПа, а температура t=60°С. Барометрическое давление равно 10325 Па (760 мм рт ст).
Решение:
Температуре t=60°С по табл. V соответствует давление рн=0.019917 МПа. Следовательно, при парциальном давлении рп=0.014 МПа пар перегрет. По табл. VI для р=0.014 МПа и t=60°С имеем
v=10.95 м3/кг.
Следовательно, абсолютная влажность рп=1/v=1/10.95=0.0913 кг/м3.
14.2. Определить абсолютную влажность воздуха, если парциальное давление в нем р=0.03 МПа, а температура t=80°С. Показание барометра В=99 325 Па (745 мм рт ст).
Ответ: rп=0.185 кг/м3.
14.3. Определить влагосодержание воздуха при температуре t=60°С и барометрическом давлении В=99325 Па (745 мм рт ст), если относительная влажность воздуха j=60%.
Решение:
По формуле: d=rп/rв,
а так как по уравнению j=рп/pн, то рп=j рн.
рн определяют по таблице V насыщенного водяного пара для температуры t=60°C. Из этой таблицы рн=0.019917 МПа и, следовательно,
рп=0.6∙0.019917=0.012 МПа.
По таблицe VI перегретого пара для р=0.012 МПа и t=60°С находим v=12.78 м3/кг. Тогда
rп=1/12.78=0.078 кг/м3.
Парциальное давление воздуха
рв=р-рп=99325-12000=87325Па=0.0873 МПа.
Плотность влажного воздуха
rв=рв/RT=0.0873∙106/287(273+60)=0.913 кг/м3.
поэтому
d=0.078/0.913=0.0854 кг/кг=85.4 г/кг.
Значение d можно также определить из формулы (279)
d=622рп/(В-рп)=622∙0.012/0.0873=85.2 г/кг.
14.4. Парциальное давление пара в атмосферном воздухе составляет 0.02 МПа, температура воздуха равна 70°С. Определить относительную влажность воздуха.
Решение:
Температуре 70°С соответствует давление рн=0.03117 МПа. Следовательно, при парциальном давлении рп=0.02 МПа пар перегрет. Из табл. VI для р=0.02 МПа и t=70 °С получаем v=7.037 м3/кг, отсюда
rп=1/v=0.127 кг/м3.
Из табл. V для t=70°С rн=r“=0.1982 кг/м3,
отсюда относительная влажность воздуха j=0.127/0.1982=64.1%.
Тот же результат получится, если из табл. V найти давление насыщения при t=70°С: рн=0.03117 МПа.
Тогда по уравнению j=рп/рн=0.02/0.03117=64.2%.
14.5. Задано состояние влажного воздуха t=80°С, рп=0.015 МПа. Определить относительную влажность, влагосодержание и плотность. Барометрическое давление В=99 325 Па (745 мм рт ст).
Ответ: j=0.31, d=108 г/кг, r=0.925 кг/м3.
14.6. Газовый двигатель всасывает 500 м3/ч воздуха при t=25°С. Относительная влажность воздуха j=0.4. Какое количество водяного пара всасывается двигателем в час?
Ответ: 4.6 кг/ч.
14.7. Состояние влажного воздуха характеризуется t=25°С и относительной влажностью j=0.8. Барометрическое давление В=99325 Па (745 мм рт ст). Найти парциальное давление пара в воздухе и его влагосодержание.
Ответ: рп=0.0025 МПа, d=16.3г/кг.
14.8. Для условий, данных в предыдущей задаче, определить степень насыщения воздуха.
Решение:
Степень насыщения воздуха определяем по формуле
j=d/dmax,
где dmax=622рн/(p-рн)=0.003166/(0.099325-0.003166)=20.5 г/кг.
Следовательно, Y=d/dmax=16.3/20.5=0.795.
Таким образом, полученные значения степени насыщения и относительной влажности j почти совпадают:
j»Y=0.8.
14.9. Наружный воздух,имеющий t=20°С и влагосодержание d=6г/кг, подогревается до температуры 45°С. Определить относительную влажность наружного и подогретого воздуха. Барометрическое давление принять равным 0.1 МПа.
Решение:
Относительную влажность воздуха находим по формуле
j=рп/рн.
Величина рн определяется по таблицам насыщенного пара и при t=20°С составляет рн=0.002337 МПа.
Парциальное давление водяного пара в воздухе при данном барометрическом давлении является функцией только влагосодержания и определяется по формуле
рп=р∙d/(622+d)=0.1∙6/628=0.00096 МПа.
Следовательно,
j1=0.00096∙100/0.002337=41%.
В процессе подогрева влагосодержание воздуха не изменяется. Следовательно, остается неизменным и парциальное давление пара. Давление насыщения рн при t=45°С по табл. V составит 0.009584 МПа, поэтому
j2=0.00096∙100/0.009584=10.01%.
14.10. Определить истинную температуру мокрого термометра tм, если сухой термометр психрометра показывает tс=35°С, а мокрый термометр-t’м=15°С. Скорость движения воздуха w=0.25 м/с.
Ответ: tм=13.4°С.
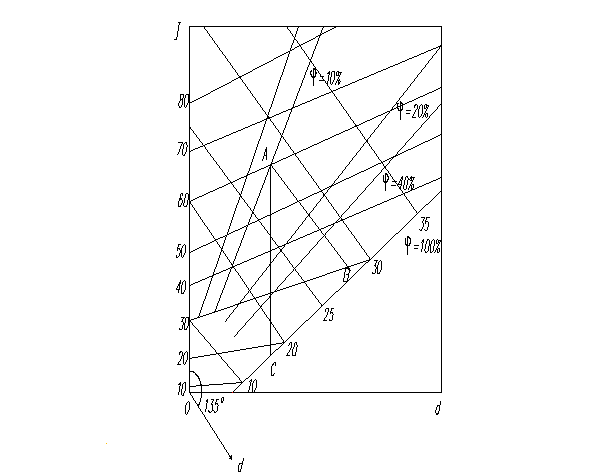
14.11. Во влажный воздух с параметрами tс=75°С и j=10% испаряется вода при адиабатных условиях. Температура воздуха при этом понижается до 45°С. Определить относительную влажность и влагосодержание воздуха в конечном состоянии. Решить с помощью диаграммы I-d рис. 14.1.
Решение:
Начальное состояние воздуха в диаграмме Id определяется пересечением изотермы t=75°С и линии j=const=10%(точка А). Так как в процессе адиабатного испарения воды температура мокрого термометра не изменяется, то конечное состояние воздуха определяется пересечением изотермы tм=45°С (точка В). Этой точке соответствуют относительная влажность j=60% и влагосодержание d=38.5 г/кг.
Рис.14.1
14.12. Состояние влажного воздуха характеризуется следующими параметрами: tc=60°С, j=10%.
Определить истинную температуру мокрого термометра и температуру точки росы.
Решение:
Заданное состояние воздуха в диаграмме Id определяется пересечением изотермы tc=60°С и кривой j=10% Рис. 14.2.
Так как истинная температура мокрого термометра есть температура адиабатного насыщения воздуха, а этот процесс характеризуется постоянством температуры испаряющейся жидкости tм=const, то проводим из точки А прямую параллельно линии tм=const до пересечения с линией j=100% (точка В). Эта точка определяет искомую температуру мокрого термометра, равную 29°С.
Для получения температуры точки росы необходимо влажный воздух охладить при постоянном давлении до состояния полного насыщения. Так как процесс охлаждения протекает при постоянном влагосодержании, то точка росы получается пересечением вертикали из точки А с кривой j=100% (точка С). Из диаграммы видно, что tр=18°С.
Рис.14. 2
14.13. В сушилку помещен материал, от которого нужно отнять 3000 кг воды. Температура наружного воздуха t1=10°С при относительной влажности j=0.4. При входе в сушилку воздух подогревается и выходит из нее при t2=40°С и j=0.85. Определить количество воздуха, которое необходимо пропустить через сушилку.
Ответ: Vн=64 500 м3.
14.14. Для использования теплоты газов, уходящих из паровых котлов, в газоходах последних устанавливают водоподогреватели (водяные экономайзеры). Минимально допустимая температура воды, поступающей в экономайзер, должна быть по крайней мере на 10° выше температуры точки росы водяных паров, содержащихся в продуктах сгорания.
Определить допускаемую температуру питательной воды, если объем продуктов сгорания Vнп.с.=9.60 м3/кг, а объем водяных паров Vнв.п.=0.24 м3/кг. Давление продуктов сгорания в газоходе экономайзера равно 0.1 МПа.
Ответ: t³30.8°С.
14.12. Психрометр, установленный в сушильной камере, показывает температуру tс=30°С и t’м=20°С. Скорость движения воздуха w=0.5 м/с. Определить состояние воздуха, если его барометрическое давление В=99 325 Па (745 мм рт ст).
Ответ: d=11.5 г/кг; j=40%.
Приложение
I. МОЛЕКУЛЯРНЫЕ МАССЫ, ПЛОТНОСТИ И ОБЪЕМЫКИЛОМОЛЕЙ ПРИ НОРМАЛЬНЫХ УСЛОВИЯХ И ГАЗОВЫЕ ПОСТОЯННЫЕ ВАЖНЕЙШИХ ГАЗОВ
| Вещество | Химии-ческое обозначе-ние | Молекул. масса µ | Плотность в кг/м3 ρ | Объем киломоля в м3/кг µυ | Газовая постоянная Дж/(кг·К) |
| Воздух | - | 28,96 | 1,293 | 22,40 | 287,0 |
| Кислород | О2 | 32,00 | 1,429 | 22,39 | 259,8 |
| Азот | N2 | 28,026 | 1,251 | 22,40 | 296,8 |
| Атмосферный азот1 | N2 | 28,16 | (1,257) | (22,40) | (295,3) |
| Гелий | He | 4,003 | 0,179 | 22,42 | 2078,0 |
| Аргон | Ar | 39,994 | 1,783 | 22,39 | 208,2 |
| Водород | H2 | 2,016 | 0,090 | 22,43 | 4124,0 |
| Окись углерода | CO | 28,01 | 1,250 | 22,40 | 296,8 |
| Двуокись углерода | CО2 | 44,01 | 1,977 | 22,26 | 188,9 |
| Сернистый газ | SО2 | 64,06 | 2,926 | 21,89 | 129,8 |
| Метан | CH4 | 16,032 | 0,717 | 22,39 | 518,8 |
| Этилен | C2H4 | 28,052 | 1,251 | 22,41 | 296,6 |
| Коксовый газ | - | 11,60 | 0,515 | 22,33 | 721,0 |
| Аммиак | NH3 | 17,032 | 0,771 | 22,08 | 488,3 |
| Водяной пар2 | H2O | 18,016 | (0,804) | (22,40) | (461,0) |
| 1 Атмосферный азот – условный газ, состоящий из азота воздуха вместе с двуокисью углерода и редкими газами, содержащимися в воздухе. 2 Приведение водяного пара к нормальному состоянию является условным. |
II. ТЕПЛОЕМКОСТЬ ОКИСИ УГЛЕРОДА
| Темпера-тура | Мольная теплоемкость в кДж/(кмоль·К) | Массовая теплоемкость в кДж/(кг·К) | Объемная теплоемкость в кДж/(м3·К) | |||||
| t в °С | µсp | µсv | µсpm | µсvm | cpm | cvm | c’pm | c’vm |
| 29,123 | 20,808 | 29,123 | 20,808 | 1,0396 | 0,7427 | 1,2992 | 0,9282 | |
| 29,262 | 20,947 | 29,178 | 20,863 | 1,0417 | 0,7448 | 1,3017 | 0,9307 | |
| 29,647 | 21,332 | 29,303 | 20,988 | 1,0463 | 0,7494 | 1,3071 | 0,9362 | |
| 30,254 | 21,939 | 29,517 | 21,202 | 1,0538 | 0,7570 | 1,3167 | 0,9458 | |
| 30,974 | 22,659 | 29,789 | 21,474 | 1,0634 | 0,7666 | 1,3289 | 0,9579 | |
| 31,707 | 23,392 | 30,099 | 21,784 | 1,0748 | 0,7775 | 1,3427 | 0,9718 | |
| 32,402 | 24,087 | 30,425 | 22,110 | 1,0861 | 0,7892 | 1,3574 | 0,9864 | |
| 33,025 | 24,710 | 30,752 | 22,437 | 1,0978 | 0,8009 | 1,3720 | 1,0011 | |
| 33,574 | 25,259 | 31,070 | 22,755 | 1,1091 | 0,8122 | 1,3862 | 1,0153 | |
| 34,055 | 25,740 | 31,376 | 23,061 | 1,1200 | 0,8231 | 1,3996 | 1,0287 | |
| 34,470 | 26,155 | 31,665 | 23,350 | 1,1304 | 0,8336 | 1,4126 | 1,0417 | |
| 34,826 | 26,511 | 31,937 | 23,622 | 1,1401 | 0,8432 | 1,4248 | 1,0538 | |
| 35,140 | 26,820 | 32,192 | 23,877 | 1,1493 | 0,8566 | 1,4361 | 1,0651 | |
| 35,412 | 27,097 | 32,427 | 24,112 | 1,1577 | 0,8608 | 1,4465 | 1,0756 | |
| 35,646 | 27,331 | 32,653 | 24,338 | 1,1656 | 0,8688 | 1,4566 | 1,0856 | |
| 35,856 | 27,541 | 32,858 | 24,543 | 1,1731 | 0,8763 | 1,4658 | 1,0948 | |
| 36,040 | 27,725 | 33,051 | 24,736 | 1,1798 | 0,8830 | 1,4746 | 1,1036 | |
| 36,203 | 27,888 | 33,231 | 24,916 | 1,1865 | 0,8893 | 1,4825 | 1,1116 | |
| 36,350 | 28,035 | 33,402 | 25,087 | 1,1924 | 0,8956 | 1,4901 | 1,1191 | |
| 36,480 | 28,165 | 33,561 | 25,246 | 1,1983 | 0,9014 | 1,4972 | 1,1262 | |
| 36,597 | 28,282 | 33,708 | 25,393 | 1,2033 | 0,9064 | 1,5039 | 1,1329 | |
| 36,706 | 28,391 | 33,850 | 25,535 | 1,2083 | 0,9115 | 1,5102 | 1,1392 | |
| 36,802 | 28,487 | 33,980 | 25,665 | 1,2129 | 0,9161 | 1,5160 | 1,1451 | |
| 36,894 36,978 | 28,579 28,663 | 34,106 34,223 | 25,791 25,908 | 1,2175 1,2217 | 0,9207 0,9249 | 1,5215 1,5269 | 1,1505 1,1560 | |
| 37,053 | 28,738 | 34,336 | 26,021 | 1,2259 | 0,9291 | 1,5320 | 1,1610 |
III. ТЕПЛОЕМКОСТЬ ВОЗДУХА
| Темпера-тура | Мольная теплоемкость в кДж/(кмоль·К) | Массовая теплоемкость в кДж/(кг·К) | Объемная теплоемкость в кДж/(м3·К) | |||||
| t в °С | µсp | µсv | µсpm | µсvm | cpm | cvm | c’pm | c’vm |
| 29,073 | 20,758 | 29,073 | 20,758 | 1,0036 | 0,7164 | 1,2971 | 0,9261 | |
| 29,266 | 20,951 | 29,152 | 20,838 | 1,0061 | 0,7193 | 1,3004 | 0,9295 | |
| 29,676 | 21,361 | 29,299 | 20,984 | 1,0115 | 0,7243 | 1,3071 | 0,9362 | |
| 30,266 | 21,951 | 29,521 | 21,206 | 1,0191 | 0,7319 | 1,3172 | 0,9462 | |
| 30,949 | 22,634 | 29,789 | 21,474 | 1,0283 | 0,7415 | 1,3289 | 0,9579 | |
| 31,640 | 23,325 | 30,095 | 21,780 | 1,0387 | 0,7519 | 1,3427 | 0,9718 | |
| 32,301 | 23,986 | 30,405 | 22,090 | 1,0496 | 0,7624 | 1,3565 | 0,9856 | |
| 32,900 | 24,585 | 30,723 | 22,408 | 1,0605 | 0,7733 | 1,3708 | 0,9998 | |
| 33,432 | 25,117 | 31,028 | 22,713 | 1,0710 | 0,7842 | 1,3842 | 1,0312 | |
| 33,905 | 25,590 | 31,321 | 23,006 | 1,0815 | 0,7942 | 1,3976 | 1,0262 | |
| 34,315 | 26,000 | 31,598 | 23,283 | 1,0907 | 0,8039 | 1,4097 | 1,0387 | |
| 34,679 35,002 | 26,394 26,687 | 31,862 32,109 | 23,547 23,794 | 1,0999 1,1082 | 0,8127 0,8215 | 1,4214 1,4327 | 1,0505 1,0618 | |
| 35,291 | 26,976 | 32,343 | 24,028 | 1,1166 | 0,8294 | 1,4432 | 1,0722 | |
| 35,546 | 27,231 | 32,565 | 24,250 | 1,1242 | 0,8369 | 1,4528 | 1,0819 | |
| 35,772 | 27,457 | 32,774 | 24,459 | 1,1313 | 0,8441 | 1,4620 | 1,0911 | |
| 35,977 | 27,662 | 32,967 | 24,652 | 1,1380 | 0,8508 | 1,4708 | 1,0999 | |
| 36,170 | 27,855 | 33,151 | 24,836 | 1,1443 | 0,8570 | 1,4788 | 1,1078 | |
| 36,346 | 28,031 | 33,319 | 25,004 | 1,1501 | 0,8633 | 1,4867 | 1,1158 | |
| 36,509 | 28,194 | 33,482 | 25,167 | 1,1560 | 0,8688 | 1,4939 | 1,1229 | |
| 36,655 | 28,340 | 33,641 | 25,326 | 1,1610 | 0,8742 | 1,5010 | 1,1296 | |
| 36,798 | 28,483 | 33,787 | 25,472 | 1,1664 | 0,8792 | 1,5072 | 1,1363 | |
| 36,928 | 28,613 | 33,926 | 25,611 | 1,1710 | 0,8843 | 1,5135 | 1,1426 | |
| 37,053 | 28,738 | 34,060 | 25,745 | 1,1757 | 0,8889 | 1,5194 | 1,1484 | |
| 37,170 | 28,855 | 34,185 | 25,870 | 1,1803 | 0,8930 | 1,5253 | 1,1543 | |
| 37,279 | 28,964 | 34,307 | 25,992 | 1,1840 | 0,8972 | 1,5303 | 1,1593 |
IV. НАСЫЩЕННЫЙ ПАР АММИАКА (НN3)
Cp=2,0599 кДж/(кг·К),k =1,32
| t в °С | p в МПа | v' в м3/кг | v" в м3/кг | s' в кДж/(кг·К) | s" в кДж/(кг·К) | i' в кДж/кг | i" в кДж/кг | r в кДж/кг |
| -50 | 0,0409 | 0,001425 | 2,623 | 3,3000 | 9,6204 | 193,4 | 1608,1 | 1414,7 |
| -45 | 0,0546 | 0,001437 | 2,007 | 3,3767 | 9,5199 | 215,6 | 1616,5 | 1400,9 |
| -40 | 0,0718 | 0,001449 | 1,550 | 3,4730 | 9,4245 | 237,8 | 1624,9 | 1387,1 |
| -35 | 0,0932 | 0,001462 | 1,215 | 3,5672 | 9,3341 | 260,0 | 1632,8 | 1372,8 |
| -30 | 0,1195 | 0,001476 | 0,963 | 3,6601 | 9,2486 | 282,2 | 1640,8 | 1358,6 |
| -25 | 0,1516 | 0,001490 | 0,771 | 3,7514 | 9,1674 | 304,4 | 1648,3 | 1344,0 |
| -20 | 0,1902 | 0,001504 | 0,624 | 3,8410 | 9,0895 | 327,4 | 1655,9 | 1328,5 |
| -15 | 0,2363 | 0,001519 | 0,509 | 3,9293 | 9,0150 | 350,0 | 1662,6 | 1312,6 |
| -10 | 0,2909 | 0,001534 | 0,418 | 4,0164 | 8,9438 | 372,6 | 1669,3 | 1296,6 |
| -5 | 0,3549 | 0,001550 | 0,347 | 4,1022 | 8,8756 | 395,6 | 1675,1 | 1279,5 |
| 0,4294 | 0,001566 | 0,290 | 4,1868 | 8,8094 | 418,7 | 1681,0 | 1262,3 | |
| 0,5517 | 0,001583 | 0,244 | 4,2705 | 8,7458 | 441,7 | 1686,4 | 1244,7 | |
| 0,6150 | 0,001601 | 0,206 | 4,3530 | 8,6838 | 465,2 | 1691,0 | 1225,9 | |
| 0,7283 | 0,001619 | 0,175 | 4,4346 | 8,6240 | 488,6 | 1695,6 | 1207,1 | |
| 0,8572 | 0,001639 | 0,149 | 4,5155 | 8,5658 | 512,5 | 1699,4 | 1186,9 | |
| 1,0027 | 0,001659 | 0,128 | 4,5954 | 8,5092 | 536,3 | 1703,2 | 1166,9 | |
| 1,1665 | 0,001680 | 0,111 | 4,6746 | 8,4563 | 581,1 | 1705,7 | 1145,5 | |
| 1,3499 | 0,001702 | 0,096 | 4,7528 | 8,3991 | 584,9 | 1708,2 | 1123,3 | |
| 1,5544 | 0,001726 | 0,083 | 4,8307 | 8,3455 | 609,2 | 1709,9 | 1100,7 | |
| 1,7814 | 0,001750 | 0,073 | 4,9078 | 8,2928 | 633,9 | 1710,7 | 1076,8 | |
| 2,0326 | 0,001777 | 0,064 | 4,9840 | 8,2400 | 659,0 | 1711,1 | 1052,1 |
V. НАСЫЩЕННЫЙ ВОДЯНОЙ ПАР (ПО ТЕМПЕРАТУРАМ)
| tв°С | p в МПа | v́ в м³/кг | v́́ в м³/кг | ρ ̋ в кг/м | i ́в кДж/кг | i “ в кДж/кг | r в кДж/кг | ś в кДж/(кг·К) | s˝ в кДж/(кг·К) | |||
| 0,01 | 0,0006108 | 0,0010002 | 206,3 | 0,004847 | 9,1544 | |||||||
| 0,0008719 | 0,0010001 | 147,2 | 0,006793 | 21,05 | 0,0762 | 9,0241 | ||||||
| 0,0012277 | 0,0010004 | 106,42 | 0,009398 | 42,04 | 0,1510 | 8,8994 | ||||||
| 0,0017041 | 0,0010010 | 77,97 | 0,01282 | 62,97 | 0,2244 | 8,7806 | ||||||
| 0,002337 | 0,0010018 | 57,84 | 0,01729 | 83,90 | 0,2964 | 8,6665 | ||||||
| 0,003166 | 0,0010030 | 43,40 | 0,02304 | 104,81 | 0,3672 | 8,5570 | ||||||
| 0,004241 | 0,0010044 | 32,93 | 0,03037 | 125,71 | 0,4366 | 8,4523 | ||||||
| 0,005622 | 0,0010061 | 26,24 | 0,03962 | 146,60 | 0,5049 | 8,3519 | ||||||
| 0,007375 | 0,0010079 | 19,55 | 0,05115 | 167,50 | 0,5723 | 8,2559 | ||||||
| 0,009584 | 0,0010099 | 15,28 | 0,06544 | 188,40 | 0,6384 | 8,1638 | ||||||
| 0,012335 | 0,0010121 | 12,04 | 0,08306 | 209,3 | 0,7038 | 8,0753 | ||||||
| 0,015740 | 0,0010145 | 9,578 | 0,1044 | 230,2 | 0,7679 | 7,9901 | ||||||
| 0,019917 | 0,0010171 | 7,678 | 0,1302 | 251,1 | 0,8311 | 7,9084 | ||||||
| 0,02601 | 0,0010199 | 6,201 | 0,1613 | 272,1 | 0,8934 | 7,8297 | ||||||
| 0,03117 | 0,0010228 | 5,045 | 0,1982 | 293,0 | 0,9549 | 7,7544 | ||||||
| 0,03855 | 0,0010258 | 4,133 | 0,2420 | 314,0 | 1,0157 | 7,6815 | ||||||
| 0,04736 | 0,0010290 | 3,408 | 0,2934 | 334,9 | 1,0753 | 7,6116 | ||||||
| 0,05781 | 0,0010324 | 2,828 | 0,3536 | 355,9 | 1,1342 | 7,5438 | ||||||
| 0,07011 | 0,0010359 | 2,361 | 0,4235 | 377,0 | 1,1925 | 7,4787 | ||||||
| 0,08451 | 0,0010396 | 1,982 | 0,5045 | 398,0 | 1,2502 | 7,4155 | ||||||
| 0,10132 | 0,0010435 | 1.673 | 0,5977 | 419,1 | 1,3071 | 7,3547 | ||||||
| 0,12079 | 0,0010474 | 1,419 | 0,7047 | 440,2 | 1,3632 | 7,2959 | ||||||
| 0,14326 | 0,0010515 | 1,210 | 0,8264 | 461,3 | 1,4184 | 7,2387 | ||||||
| 0,16905 | 0,0010569 | 1,036 | 0,9652 | 482,5 | 1,4733 | 7,1832 | ||||||
| 0,19854 | 0,0010603 | 0,8917 | 1,121 | 503,7 | 1,5277 | 7,1298 | ||||||
| 0,23208 0,27011 0,3130 0,3614 0,4155 0,4760 0,5433 0,6180 0,7008 0,7920 0,8925 1,0027 1,1234 1,2553 1,3989 1,5551 1,7245 1,9080 2,1062 2,3201 2,5504 2,7979 3,0635 3,3480 3,6524 3,9776 | 0,0010649 0,0010697 0,0010747 0,0010798 0,0010851 0,0010906 0,0010962 0,0011021 0,0011081 0,0011144 0,0011208 0,0011275 0,0011344 0,0011415 0,0011489 0,0011565 0,0011644 0,0011726 0,0011812 0,0011900 0,0011992 0,0012087 0,0012187 0,0012291 0,0012399 0,0012512 | 0,7704 0,6663 0,5820 0,5087 0,4461 0,3926 0,3466 0,3068 0,2725 0,2426 0,2166 0,1939 0,1739 0,1564 0.1409 0,1272 0,1151 0,1043 0,09465 0,08606 0,07837 0,07147 0,06527 0,05967 0,05462 0,05006 | 1,298 1,496 1,718 1,966 2,242 2,547 2,885 3,258 3,,670 4,122 4,617 5,750 6,157 6,394 7,097 7,862 8,688 9,588 10,56 11,62 12,76 13,99 15,32 16,76 18,30 19,98 | 525,0 546,3 567,5 589,0 610,5 632,2 653,9 675,5 697,3 719,2 741,1 763,1 785,2 807,5 829,9 852,4 875,0 897,7 920,7 943,7 966,9 990,4 1013,9 1037,5 1061,6 1085,7 | 1,5814 1,6345 1,6869 1,7392 1,7907 1,8418 1,8924 1,9427 1,9924 2,0417 2,0909 2,1395 2,1876 2,2357 2,2834 2,3308 2,3777 2,4246 2,4715 2,5179 2,5640 2,6101 2,6561 2,7021 2,7478 2,7934 | 7,0777
7,0272
6,9781
6,9304
6,8839
6,8383
6,7940
6,7508
6,7081
6,6666
6,6256
6,5858
6,5465
6,5074
6,4694
6,4318
6,3945
6,3577
6,3212
6,2849
6,2488
6,
Поиск по сайту©2015-2024 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование. Дата создания страницы: 2016-04-26 Нарушение авторских прав и Нарушение персональных данных |
Поиск по сайту: Читайте также: Деталирование сборочного чертежа Когда производственнику особенно важно наличие гибких производственных мощностей? Собственные движения и пространственные скорости звезд |