Второй тип задач является обратным по отношению к первому. Одной из задач второго типа может быть, например, следующая: при заданной точечной характеристике поля, заданной форме и расположении электродов и свойствах среды найти интенсивность источников, создающих это поле.
Задачи расчета электрического поля в проводящей среде могут быть решены:
1) непосредственным интегрированием уравнений, описывающих поле (см. примеры 200 и 202);
2) использованием аналитических решений для других статических невихревых полей (см. примеры 204 и 203);
3) экспериментальным (см. § 20.8) или графическим путем; графический метод построения картины поля применительно к плоскопараллельному электростатическому полю рассмотрен в § 19.44, а к плоскомеридианному полю — в § 19.45; изложенная в этих параграфах методика пригодна и для построения картины плоскопараллельного и плоскомеридианного электрического полей в проводящей среде;
4) методом зеркальных изображений, в соответствии с аналогией, рассмотренной в § 20.7, формулы для расчетных токов I2 и I3 в задаче, дуальной задаче § 19.32, следуют из формул для т2 и т3, если в них е1а заменить на y1 а ε2а — на у2. Метод применим и в том случае, когда проводимость γ2 = 0.
Применительно к электрическому полю проводящей среды вводят понятия собственных и взаимных проводимостёй тел, определяемых но аналогии с собственными и взаимными емкостями тел (частичными емкостями — см. § 19.34);
-5) методом конформных преобразований (см. приложение И).
§ 20.11. Расчет электрического поля в диэлектрике, окружающем проводники с токами. Принято считать, что картина электрического поля в диэлектрике, окружающем проводники с токами, тождественна картине электрического поля в условиях электростатики.
|
|
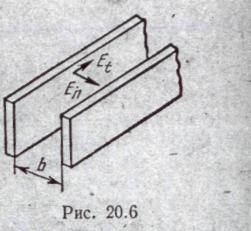Строго говоря, это верно лишь приближенно, так как в условиях электростатики тангенциальная составляющая напряженности электрического поля на поверхности проводящего тела равна нулю, тогда при протекании постоянного тока по проводнику тангенциальная составляющая напряженности электрического поля на поверхности проводника, хотя и очень мала по сравнению с нормальной составляющей напряженности в той же точке, но не равна нулю. На числовом примере убедимся в том, что тангенциальная составляющая напряженности поля Е( во много раз меньше нормальной составляющей напряженности поля Еп.
Положим, что разность потенциалов, U между
двумя параллельными токонесущими медными
Пример 199. Определить ток утечки коаксиального кабеля на 1 км длины. Пространство между жилой и оболочкой заполнено неидеальным диэлектриком, который обладает проводимостью у = 10-8 Ом-1 
м-1.Радиус жилы rи радиус оболочки r2 = еr1 где е — основание натуральных логарифмов. Напряжение между жилой и оболочкой 10 кВ. Решен и е. Ток утечки I = UG. Проводимость
Ток утечки через несовершенную изоляцию I= 104 0,628 10-4 = =0,628 А/км.
Пример 200. Рассмотрим простейшую задачу расчета поля заземления. Подвод тока к земле производится с помощью погруженных в землю заземлений. Ток стекает через заземлитель в землю и расте-: кается по ее толще, с тем чтобы собраться у другого электрода заземлителя. Земля выполняет роль обратного провода.
Если погрузить в землю металлическую полусферу, через которую в землю стекает ток I (рис. 20.7), и принять, что второй электрод,, к которому будет подтекать ток, находится очень далеко, то плотность тока в земле на поверхности полусферы радиусом R будет 
= I/2πR2 (поверхность сферы 4πR2, поверхность полусферы 2πR2).
|
|
Напряженность поля
На рис. 20.7 изображена кривая изменения потенциала на поверх-
ности земли.
|
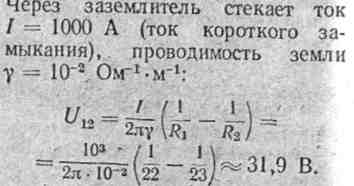Найдем напряжение между точками 1 и 2, расположенными на расстоянии, примерно равном шагу человека (R1 = 22 м, R2 = 23 м).
Пример 201. В морскую воду при γ = 0,1 Ом-1 
м-1 вертикально опущены две металлические трубы
наружным диаметром 5 см и длиной 3 м. Найти проводимость G между трубами. Оси труб удалены на расстояние d = 25 м. Решение.
Пример 202. Вывести формулу для определения проводимости G между плоскостями S1 И S2 проводящего тела проводимостью, γ имеющего форму клина (рис. 20.8).
|
|
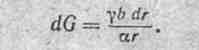
| Проводимость |
|
Решение. Проводимость заштрихованного пояска высотой rα, толщиной dr и шириной b:
Пример 203. В пластинке из алюминия (γе = 3,57 107 Ом-1-м-1) создано равномерное электрическое поле напряженностью E0 = 0,1 В/м. Определить плотность тока в медном теле (yt = 5,6 107 Ом-1 м_1), имеющем цилиндрическую форму и расположенном перпендикулярно полю.
Пример 204. Используя результат примера 195, вывести формулу для определения проводимости заземления, выполненного в виде
стальной трубы длиной l, радиусом r, забитой в землю перпендикулярно ее поверхности. Полагать, как и в примере 200, что второй электрод находится в бесконечности, удельная проводимость земли у, Lir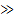 
1.
Решение. Картина поля заземлителя показана на рис. 20.9. Труба длиной L, находящаяся в земле, на рисунке дополнена такой же трубой, находящейся в воздухе. Проводимость зазем
|
|
Вопросы для самопроверки
1. Почему уравнение 
= у (Е + EСтор) называют обобщенным законом Ома» а также вторым законом Кирхгофа? 2. Почему несправедливо уравнение 
2φ =0
для поля, в котором проводимость у есть функция координат? 3. Обоснуйте возможность моделирования электростатического поля полем постоянного тока в проводящей среде. 4. Каким образом можно приспособить аналитические решения задач электростатики для решения родственных задач в поле проводящей среды? Приве-
дите примеры. 5. Составьте аналоги трем группам формул Максвелла для поля постоянного тока в проводящей среде. 6. Металлический шарик радиуса R окружен бесконечно протяженной проводящей средой с проводимостью у; с шарика в среду стекает ток / (второй электрод в бесконечности); определите энергию в единицу вре-
мени, доставляемую источником (ответ: 
27. В неоднородной проводящей среде
с проводимостью γ(х, у, z) и диэлектрической проницаемостью 
(х, у, z) обеспечивается неизменное распределение плотности тока (х, у, z). Определите объемное
.распределение зарядов рсвоб (ответ:.рСВОб = 
(gradεа - 
grad γ) 8.Решите
задачи 20.2; 20.6; 20.8; 20.11; 20.14; 20.17; 20.24.
ГЛАВА ДВАДЦАТЬ ПЕРВАЯ
МАГНИТНОЕ ПОПЕ ПОСТОЯННОГО ТОКА
§ 21.1. Связь основных величин, характеризующих магнитное поле. Механические силы в магнитном поле. Магнитное поле постоянного тока это одна из компонент электромагнитного поля, не изменяющегося во времени. Оно создается неизменными во времени токами,
протекающими по проводящим телам, неподвижным в пространстве по отношению к наблюдателю. Хотя при протекании постоянных токов имеется и вторая компонента электромагнитного поля, а именно электрическое поле, но оно во времени не изменяется и потому не влияет на магнитное поле. Благодаря этому магнитное поле постоянного тока можно рассматривать независимо от электрического.
Магнитное поле характеризуется индукцией В, намагниченностью j
|
| где µ0— магнитная постоянная, в системе СИ равная 4π-10-7 Гн/м; µ— относительная магнитная проницаемость; µа — абсолютная магнитная проницаемость. |
|
и напряженностью магнитного поля Н. Эти три величины связаны соотношением:
Одним из основных проявлений магнитного поля является воздействие его на проводник с током, помещенный в это поле **. Опыт показывает, что сила F, с которой магнитное поле действует на элемент проводника длиной dl с током I, определяется следующим образом:
F = I[dlB]. (21.2)
Эта сила направлена перпендикулярно индукции в данной точке поля и перпендикулярна элементу тока I dl (рис. 21.1, а).
Если индукция В и элемент длиной dl параллельны, то элемент тока не испытывает механического воздействия со стороны магнитного поля. Механическое воздействие магнитного поля на элемент тока максимально, когда В и dl взаимно перпендикулярны.
Из (21.2) следует, что индукция — это силовая характеристика поля, определенная при условии, что внесенный в данную точку поля элемент тока I dl, расположенный перпендикулярно В, не исказил магнитного поля, существовавшего до внесения в эту точку элемента
--------------------------------------
* Пояснения к формуле (21.1) см. в § 14.24. ** А в более общем случае воздействие его на движущийся заряд (§ 2.30).
 тока. Другими словами, при оговоренном расположении элемента тока индукция численно определяется так —
|
Имея в виду это условие не gискажения поля внесением элемента тока, соответствии с (21.2) говорят также, что индукция может быть опре- делена как сила, действующая на проводник длиной dl, равной единице, если по нему протекает ток I, равный единице.
В СИ единицей измерения индукции является тесла (1 Т = 1В • с/м2) в системе С ГСМ — гаусс — Гс.
Механическое воздействие магнитного поля на ток можно пояснить, исходя из представления о деформации силовых, линий магнитного поля или из понятия о силах Лоренца (§ 2,30). Деформация силовых линий иллюстрируется рис. 21.1,6 — г. На рис. 21.1 изображены: б — силовые линии равномерного магнитного поля до внесения в него провода с током; в — силовые линии уединенного провода с током;
г — силовые линии результирующего поля. Слева от провода силовые линии собственного поля провода направлены встречно силовым линиям внешнего равномерного поля, а справа — согласно с ним. Поэтому результирующее поле слева от провода разрежено, а справа сгущено. Силовые линии, стремясь выпрямиться, производят давление на провод справа налево.
Обратим внимание на то, что силовая линия, показанная пунктиром на рис. 21.1, г, является как бы граничной между силовыми линиями, расположенными справа и слева от провода. В точке с этой линии магнитная индукция равна нулю.
При взаимно перпендикулярном, расположении магнитного поля и провода с током направление действия силы часто определяют по мнемоническому правилу, получившему название правила левой руки; если расположить левую руку таким образом, что силовые линии будут входить в ладонь, вытянутые пальцы направить по току, то отогнутый большой палец покажет направление действующей силы. Взаимодействие поля с током имеет место независимо от причин возникновения магнитного поля, в результате ли протекания макротоков в электрических контурах, или вследствие протекания микро--
токов в ферромагнитных материалах, или потока электронов в вакуумном приборе и т. п. Оно наблюдается как в постоянном, так и в изменяющемся во времени поле *.
Пример 205. На рис. 21.1, д изображены два параллельных прохода, расстояние между которыми а — 10 см. По первому проводу
течет ток 11 — 1000 А, по второму I2 = 500 А (направления токов показаны стрелками). Определить силу взаимодействия между проводами на длине 1м.
Решение. Воспользуемся формулой (21.2). Учтем, что угол
между элементом длины второго провода dl и индукцией В от левого
-----------------------------------------------
* В § 21.28 показано, что силу можно определить как производную от энергии магнитного поля по изменяющейся координате контура с током.
провода равен 90°. Поэтому модуль векторного произведения [dlB] равен dl В sin 90° = dl В.
Магнитная индукция, создаваемая первым проводом в точках, где расположен второй провод, по закону полного тока B=µ0I1/2πа
Сила
Под действием силы провода стремятся сблизиться.
§21.2 Интегральная форма закона полного тока. Количественная связь между циркуляцией вектора H по замкнутому контуру и током внутри контура определяется законом полного тока в интегральной форме —- линейный интеграл от напряженности магнитного поля
вдоль любого замкнутого контура равен пол
ному току, пронизывающему замкнутый кон
тур:,
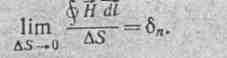
Hdl =I. (21.3)
Под полным током, понимают весь ток (ток проводимости и ток смещения), пронизывающий контур интегрирования.
Интегральную форму закона полного тока применяют, когда может быть использована симметрия в поле. Так, например, напряжен-
ность поля в некоторой точке А в поле уединенного прямого провода с током / (рис. 21.2) по закону полного тока определяют следующим образом. Проведем через точку А окружность радиусом R в плоскости, перпендикулярной оси провода, так что центр ее находится на этой оси. В силу симметрии напряженность поля во всех точках окружности численно одна и та же. Направление напряженности совпадает с касательной к окружности. Поэтому
Hdl = Hdlcos0° = H dl = H 
2πR = I; H =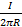 
С увеличением радиуса R напряженность магнитного поля убывает по гиперболическому закону.
Если какое-либо поле имеет сложный характер и не удается составить замкнутый контур, все точки которого находились бы в симметричных условиях, то хотя интегральная форма записи закона полного тока справедлива и для такого контура, использовать ее для нахождения напряженности в любой точке поля так просто не удается
(H нельзя вынести из-под знака интеграла).
§ 21.3. Дифференциальная форма закона полного тока. Соотношение (21.3) пригодно для контура любых размеров, в том числе и для весьма малого.
Выделим в какой-либо среде небольшой контур («жирно» обведен
на рис. 21.3) и составим вдоль него циркуляцию вектора H. Цирку-
ляция напряженности поля вдоль этого контура равна току, прони
зывающему обведенную площадь.
Если площадь мала, то можно полагать, что плотность тока в пре-
делах этой площади одинакова и тогда ток, пронизывающий площадь,
== 
S = 
nS. Здесь n— проекция вектора плотности тока 
на нормаль к площади, т. е. на направление 
S; Н dl = nS.
| направление движения острия правого винта головка которого вращается в направлении, принятом за положительное. при обходе контура и составлении циркуляции.
Разделим обе части равенства на S и устремим S к нулю. Это будет соответ ствовать стягиванию рассматриваемой площади щади к нулю. Предел полученного отно- 'Щенпя, _\,
|
За положительное направление нормали к площади принимают
щади к нулю. Предел полученного отношения
В левой части равенства находится величина, которая является
роекцией ротора H на направление нормали к площади S. Следо-
ательно, rotn H = n
Если площадь S ориентировать в пространстве так, что напра-
ление нормали к ней совпадет с направлением вектора плотности
ока б в данной точке поля, то тогда вместо равенства проекций двух
екторов (rotn H и n) можно записать равенство самих векторов
rotn H = (21.4)
Формула (21.4) и представляет собой закон полного тока в дифференциальной форме.
Ротор — это функция, характеризующая поле в рассматриваемой точке в отношении способности к образованию вихрей.
Уравнение (21.4) записано в общей форме, безотносительно к системе координат, и в каждой конкретной системе координат оно раскрывается по-своему.
§21.4. Раскрытие выражения rot H — 
в декартовой системе | координат. Равенство двух векторов rot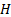 
и означает, что равны проекции их на ось х, проекции на ocь y и проекции на ось z. Проекция rot H на ось z равна rot z H = H 
dl проекция вектора на ось
sz 
0 sz
z есть 
и и т. д.
На рис. 21.4 в декартовой системе координат изображен малый прямоугольный контур mnpq. Обойдем этот контур против часовой
стрелки и составим циркуляцию вектора H; при ее составлении необходимо учесть, изменение вектора H от точки к точке. Обозначим проекции H на оси х и у в точке т соответственно через Нх и Hy.
при составлении циркуляции на участках тп и рq необходимо принимать во внимание лишь «иксовые» составляющие H («игрековые» составляющие перпендикулярны элементу пути).
Составляющую 
Н dl на участке тп находят как произведение среднего значения «иксовой» составляющей напряженности на этом
участке на длину пути dх
§.21.5. Запись ротора в виде векторного произведения. Формально rot 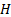можно представить в виде векторного произведения оператора пространственного дифференцирования 
на вектор H, т. е. rot H = 
В этом нетрудно убедиться путем непосредственного умножения 
§ 21.6. Раскрытие rot Н в виде определителя в декартовой системе. Ротор любого вектора, используемого в теории электромагнитного поля, можно представить в виде определителя третьего порядка. Так, rot H в декартовой системе записывают в виде следующего определителя:
Непосредственное раскрытие определителя показывает, что получается выражение (21.5).
§ 21.7. Выражение проекций ротора в цилиндрической и сферической системах координат. Без вывода приведем выражение проекций
ротора H:
| всферической системе координат: |
в цилиндрической системе координат:
§ 21.8. Принцип непрерывности магнитного потока и запись его в дифференциальной форме. Магнитный, поток есть поток вектора магнитной индукции через некоторую поверхность: Ф = ∫ В dS.
. S.
Индекс S под знаком.интеграла свидетельствует о том, что интеграл взят по поверхности S. Если поверхность замкнута сама на себя (например, поверхность шара), то поток, пронизывающий замкнутую поверхность, Ф = BdS.
Опыт показывает, что вошедший внутрь любого объема магнитный поток равен магнитному потоку, вышедшему из того же объема.
Следовательно, алгебраическая сумма вошедшего в объем и вышедшего из объема потоков равна нулю:
BdS. = 0. (21.9)
Выражение (21.9) представляет собой математическую запись прин-
ципа непрерывности магнитного потока.
Разделим обе части (21.9) на объем V, находящийся внутри замк-
нутой поверхности S, и найдем предел отношения, когда объем V
стремится к нулю:
Соотношение (21.10) можно трактовать как дифференциальную форму принципа непрерывности магнитного потока. Оно пригодно для любой точки магнитного поля. Следовательно, в любой точке этого поля нет ни истока, ни стока линий вектора магнитной индукции. Линии вектора Д нигде не прерываются, они представляют собой замкнутые сами на себя линии (окружность — пример замкнутой на себя линии).
Но линии H в точках, где изменяется j (например, на границах сред с разными
µ.), прерывны. Это следует из (21.10); div В — divµ0 (H+j).= 0. Отсюда div H = —div J. Сопоставьте с прерывностью линий Е и непрерывностью линий D в электрическом поле (см. § 19.39)., -
§21.9. Магнитное поле в областях «занятых» и «не занятых» постоянным током. Вихревыми принято называть поля, ротор которых отличен от нуля. Так как для магнитного поля постоянного тока rot H= , то во всех. точках пространства, где 
0, поле вектора H является вихревым. В областях пространства, где = 0, rot H = 0, магнитное поле можно рассматривать как потенциальное,
§ 21.10. Скалярный потенциал магнитного поля. Для совокупности точек, где = 0, rot H= 0,магнитное поле можно рассматривать как потенциальное, т. е. как поле, каждая точка которого имеет скалярный магнитный потенциал φм. Следовательно, для таких областей можно принять
H=-gradφм
Так как div В = div µa H = 0, то при µa = const div H= 0. Подставив в последнее выражение —grad φм, вместо H, получим div grad φм, = 0.
Таким образом, скалярный потенциал магнитного поля φм, о котором может идти речь, только для областей, не занятых током, под-
чиняется уравнению Лапласа:
2φм= 0. (21.12) '
Разность скалярных магнитных потенциалов между точками 1 и 2 называют падением магнитного напряжения между точками 1 и 2
(см. стр. 352): UM12 = φм1- φм2 = ∫2 H dl.
Падение магнитного напряжения между точками 1 и 2 по какому-то одному пути (например, по пути 132, рис. 21.5, а) равно падению маг- нитного напряжения между теми же точками по какому-то другому
пути (например, по пути 142) в том случае, когда эти пути образуют замкнутый контур, ток внутри которого равен нулю.
Если же замкнутый контур, образованный двумя путями, охватывает; некоторый ток, то падение магнитного напряжения по первому пути не равно падению магнитного напряжения по второму пути — они будут различаться на величину тока, охваченного контуром. Последнее вытекает из закона полного тока. Так, применительно к рис. 21.5, a ∫ Hdl 
∫ Hdl (ибо из закона полного тока следует,