построение картины плоскопараллельного поля. 7 глава

Ψ=∑M_kJ_k, l_k

где M_k —взаимная индуктивность катушки k с контуром а.

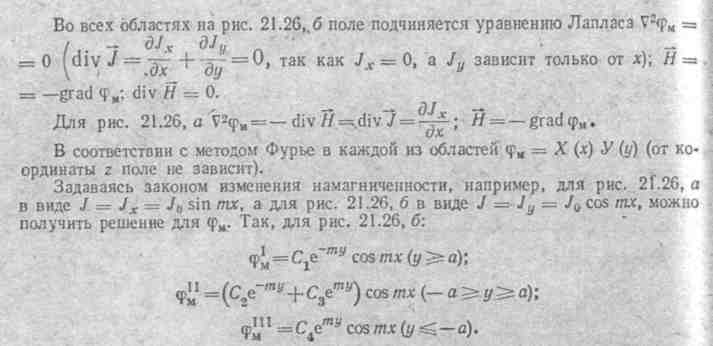
§ 21.28. Выражение механической силы в виде производной от энергии маг­
нитного поля по координате. Положим, что в системе из п контуров с токами

один из контуров под действием механической силы F на него со стороны остальных.контуров перемещается так, что координата х его изменяется на величину dx. Требуется выяснить, какая связь существует между силой F и изменением энергии магнитного поля системы dW_M Для какого-то контура.системы запишем уравнение по 2-му закону Кирхгофа:

Все цепи от источников э.д.с.3 за вычетом тепловых потерь.

При перемещении какого-то контура на расстояние dx изменяется магнитная. энергия системы W_м на величину dW_м и совершается механическая работа Fdx, где F — составляющая силы, действующая по направлению.

Из закона сохранения энергии следует, что энергия, доставляемая источниками э.д. с. за время dt, должна равняться энергии, выделяющейся за то же время в виде

Теплоты в сопротивлениях контура, плюс энергия, которая затрачена на покрытие механической работы F dx, плюс приращение энергии магнитного поля dW_M

торую последние отдают в цепи, за вычетом тепловых потерь. Из (21.46).получим:

Из уравнения (21.47) вытекают два частных случая.

1. Если перемещение происходит таким образом, что потокосцепления контуров остаются неизменными, то d 𝜓 _k =0_,Fdx = - dW_м
и

2. Если перемещение происходит так, что токи в контурах остаются неизмен­ными {i_k = const), что возможно, например, когда перемещение происходит на­столько быстро, что токи не успевают измениться, то в соответствии с § 2.10 W_H =1/2Σί_kd𝜓_k Следовательно,

Во втором частном случае выражение для механической силы отличается от (21.18) только знаком.

При i_k = const доставляемая в цепи от источников э. д. с; энергия за выче­том тепловых потерь делится на две равные части. Одна идет на приращение энергии магнитного поля: dW_м, Другая — на механическую работу F dx. Уравнения. (21.48) и (2.1,50) часто используют для нахождения механической силы. Чтобы найти силу. F, надо либо составить аналитическое выражение для магнитной энергии си­стемы и продифференцировать его по изменяющейся координате, либо опытным путем снять зависимости магнитной энергии, от изменяющейся координаты и затем графически продифференцировать её. Если в поле двух катушек при изменении координаты индуктивности

L ₁ и L₂ остаются постоянными и меняется только взаимная индуктивность М, то F ' = I₁ I₂

Вопросы для самопроверки 1. Дайте определение магнитного поля постоянного тока. Какими точечными и интегральными величинами оно характеризуется? 2. Каков физический смысл векторов В, J,H? Каковы единицы измерения их? 3. Какие поля называют вихревыми? 4ч В каких случаях величина Н может быть определена без затруднений при помощи закона полного тока? 5. Дайте физическое толкование понятию ротора. 6. Запишите принцип непрерывности магнитного потока в интегральной и дифференциальной формах. 7. Могут ли линии Н быть прерывными? 8.. Почему понятие (φ_м неприменимо к областям, занятым током? 9. Может ли φ_м, бесконечно близко расположенных точек в поле линейного тока І различаться на конечную величину? 10. Почему вектор-потенциал А является более общей характеристикой поля, чем φ_м? 11. На каком основании можно принять В = rot А? 12. Определите характер распределения плотности тока δ в некоторой области, если в ней А= i5x³. Ответ: .

13. Какого типа соответствия могут быть в картинах магнитного и электростатического полей? 14. Поясните ход решения задачи о цилиндрическом магнитном экране и расскажите, из каких соображений находят постоянные интегрирования. 15. Чем можно объяснить, что в соответствующих формулах на метод зеркальных изображений для сходных задач в магнитном (§ 21.23) и электростатическом (§ 19.32) полях^: индексы 1 и 2 поменялись местами? 16. Почему можно сказать, что закон Био —Савара — Лапласа в некотором смысле является более общим, чем закон полного тока? 17. Ток І проходит по отрезку дуги окружности радиуса а с центральным углом α. Определите H в центре окружности ответ: Іα/4πа 18. Решите задачи 21.1;
21.4; '21.12; 21.21; 21.24; 21.25..

ГЛАЗА ДВАДЦАТЬ ВТОРАЯ

ОСНОВНЫЕ УРАВНЕНИЯ ПЕРЕМЕННОГО ЭЛЕКТРОМАГНИТНОГО ПОЛЯ

Подставим (21.49) в (21v47), получим

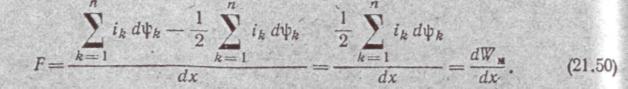
§ 22. Определение переменного электромагнитного поля. Под переменным электромагнитным полем понимают совокупность изме­няющихся во времени и взаимно связанных и обусловливающих друг друга электрического и.магнитного полей. Оно определяется двумя векторными величинами — напряженностью электрического поля Е и напряженностью магнитного поля Н.

Переменное электромагнитное поле является одним из видов материи. Оно обладает энергией, массой, количеством движения, сможет превращаться в другие виды материи и самостоятельно сущест­вовать в виде электромагнитных волн. Любые возмущения поля в диэлектрике с огромной скоростью, для вакуума равной примерно 3 10⁸ м/с, передаются на большие расстояния.

При исследовании процессов в переменном электромагнитном поле пользуются уравнениями Максвелла.

Систему уравнений Максвелла образуют четыре уравнения *
1) уравнение (22.1), выражающее связь между ротором напряжен­
ности магнитного поля и плотностью тока в той же точке поля, — пер­-
овое уравнение Максвелла;.

2) уравнение (22.4), которое определяет связь между ротором напряженности электрического поля и скоростью изменения магнит­ного поля в той же точке поля, — второе уравнение Максвелла;

3) уравнение div В — 0, выражающее принцип, непрерывности

магнитного потока [оно следует из (22.4) после взятия от обеих частей его дивергенции];

4) уравнение div Е = р_своб/ε_а, выражающее связь между истоком напряженности электрического поля и плотностью свободных зарядов в той же точке поля.

Эту систему дополняют уравнением непрерывности (см. § 22.3) и теоремой Умова-— Пойнтинга (см. § 22.6).

______________________________

* Уравнения были сформулированы английским ученым Д. Максвеллом (1831— 1879). в его книге «Трактат об электричестве и магнетизме», изданной в 1873 г.

§ 22.2. Первое уравнение Максвелла. Первое уравнениеМаксвела записывают следующим образом   Максвелла записывают следующим образом:

■

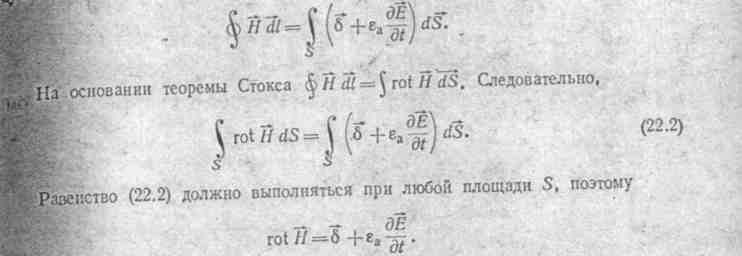
В правой части его имеются две плотности тока: плотность тока проводимости и плотность тока электрического dD/dt. Ток электрического смещения возникает в любом диэлектрике, в том числе и в. вакууме, при изменении напряженности электрического поля во времени. Ток смещения порождает магнитное поле так же, как и ток проводимости. Хотя природа тока проводимости и тока смещения неодинакова, оба они обладают одним и тем же свойством — вызывать магнитное поле.

Таким образом, смысл первого уравнения Максвелла состоит

в том, что всякое изменение электрического смещения во времени (dD/dt)

в некоторой точке поля (т. е. возникновение в ней тока смещения) на таких же правах, как и ток проводимости, вызывает в этой точке вихрь магнитного поля (rot H), т. е. вызывает вихревое магнитное поле. Если среда однородна и изотропна, то ε_а = const и тогда

С током смещения в предыдущих разделах (особенно в гл. 3 и 8) приходилось встречаться неоднократно. Так, известно,что при зарядке конденсатора через него протекает ток. Этот ток протекает через диэлектрик и является током смещения. Если, например, взять незаряженный плоский воздушный конденсатор и подключить его к источнику э. д. с. напряжением U через сопротивление R, то напряжение на обкладках конденсатора будет

Через поверхность S ток смещения в S раз больше, т. е. он равен току проводимости, протекающему по проводникам, соединяющим конденсатор с источником э. д. с.Отметим, что первое уравнение Максвелла представляет собой закон полного тока в дифференциальной форме.

Убедимся в том, что из закона полного тока следует уравнение (22.1). С этой целью возьмем произвольный контур и составим для него уравнение по закону полного тока. Полный ток, пронизывающий площадь, ограниченную контуром, равен сумме тока проводимости и тока смещения. Поэтому

§ 22.3. Уравнение непрерывности. Линии полного тока

являются непрерывными. Физически это означает, что на границе проводящей среды и диэлектрика ток проводимости переходит в ток смещения.

Можно математически сформулировать принцип непрерывности

(замкнутости) линий полного тока. С этой целью от обеих частей (22,1) дивергенция от ротора тождественно равна нулю (см. § 21.12).

Уравнение непрерывности (22.3') называют также законом сохранения заряда. Этот закон означает, что электрический заряд неуничтожаем, он может только перемещаться из одного места в другое.

§ 22.4. Второе уравнение Максвелла. Второе уравнение Максвелла

записывают следующим образом:

 

Физический смысл его состоит в том, что всякое изменение магнитного

 

поля во времени (dB/dt) в какой-либо точке поля возбуждает вихрь или

 

ротор электрического поля в той же точке поля, т. е. вызывает вихревое

 

электрическое поле

 

Второе уравнение Максвела представляет собой дифференциальную форму закона электромагнитной индукции.

Для того чтобы убедиться в этом, проведем следующие рассуждения. Мысленно возьмем некоторый замкнутый контур, расположенный в переменном электромаг нитном поле. Переменный магнитный поток, пронизывающий контур, наведет в нем. э.д.с.

Равенство (22.5) должно выполняться при любых площадях S, что возможно только в том случае, когда равны подынтегральные функции- обоих интегралов. Следовательно,

rot E=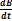

Знак «минус» в правой части второго уравнения Максвелла (как и в формуле

е= - d𝜓/dt) объясняется тем, что в основу положено правило правого винта. Если завинчивать правый винт так, что положительное направление вектора.магнитной индукции В в некоторой точке пространства при возрастании индукции этой точке совпадет с направлением движения острия винта, то положительное направление:для вектора напряженности электрического поля E при составлении циркуляции вектора Е вдоль бесконечно малого контура, окружающего эту точку и лежащего,в плоскости, перпендикулярной вектору В, совпадет с направлением вращения го-
ловки винта.

Знак «минус» в правой части (22,4) поставлен для того,_г чтобы привести в соответствие действительное направление для E при оговоренных ранее условиях с направлением, принятым для E за положительное.

Как в первом, так и во втором уравнениях Максвелла участвуют
частные (не полные) производные во времени. Объясняется это тем,
что уравнения Максвелла записаны для таких тел и контуров, кото­
рые неподвижны по отношению к выбранной системе координат.
(Вопросы электродинамики движущихся сред кратко рассмотрены
в § 22.9.)

В переменном электромагнитном поле кроме силовых линий элект-, рического поля, «начинающихся» и «оканчивающихся» на электриче- ских зарядах (как в электростатическом поле) могут быть и замкнутые на себя силовые линии электрического поля, охватывающие замкнутые на себя силовые линии магнитного Поля (см., например, рис. 26.5, а).

§ 22 5 Уравнения Максвелла в комплексной форме записи. Уравнения (22 .1) и (22 4) записаны для мгновенных значении. Если H и E изменяются во времени синусоидально, то можно воспользоваться символическим методом и записать эти уравнения (22.1) и (22 4) в иной форме. Пусть H = Н_т sin ( ωt+ 𝜓_н) и Е. = Е_т sin (ωt+ 𝜓_E ). Можно записать Н= Im H_me^iωt(Im - мнимая часть) или, условно H H_me^iωt где комплексная амплитуда H_m= H_m e^i𝜓n. ^В свою очередь Е E_me^iωt значок соответствия). Так как напряженности Е и H, кроме того, что они меняются во семени по синусоидальному закону, являются функциями векторными т.е. определенным образом ориентированными в пространстве векторами то над ними ставят стрелку и точку: Ё_т и Н_т. Стрелка означает, что речь идет о векторе в пространстве, точка - о том что проекции этого вектора на любую из координатных осей во времени изменяются синусоидально. Тогда можно заменить на γ Ee^iωt и

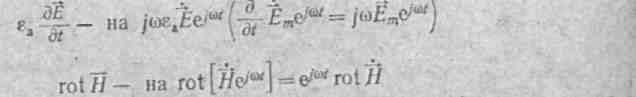
(e^iωt как постоянную величину, не зависящую от координат, можно вынести за знак ротора). При этом первое уравнение Максвелла запишем так

§ 22. 6 Теорема Умова - Пойнтинга для мгновенных значений.

Кроме уравнений Максвелла, большое значение в теории электро-

магнитного поля имеет теорема Умова - Пойнтинга, которая описывает

энергетические соотношения в поле.

Теорема Умова – Пойнтинга имеет две формы записи: первая -для мгновенных значений, вторая - комплексная форма - для синусоидально изменяющихся величин

 

.

Для сокращения записи обозначим векторное произведение Е на Н через П, т. е. примем, что П = [ЕН]; П — это вектор, называемый

вектором Пойнтинга; размерность его равна

произведению размерностей E и Н:

[П]=[Е][Н]= =ВА/м²

Таким образом, вектор Пойнтинга имеет размерность мощности (или энергии в единицу времени), отнесенной к единице поверхности, и направление его (рис. 22.1) совпадает с на­правлением движения острия правого винта.

если головку последнего вращать по кратчайшему направлению от Е к Н. Следовательно,

Распространим (22.11) на некоторый объем конечных размеров. С этой целью проинтегрируем (22.11) по объему V:

______________________________
Подобно тому, как поверхностный интеграл по теореме Стокса преобразовывается в линейный (см. § 21.14): ∫ rotАdS = ∮Adl,

s

объемный интеграл в свою очередь может быть преобразован в поверхностный. Это преобразование осуществляют с помощью теоремы

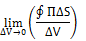
, где — элемент поверхности объема , а знак ∑ означает суммирование по всем поверхностям объема . Тогда

∫ divПdy=∑∑ =∑∑П 𝜟𝙎

𝙑

Пёрвый знак суммы означает суммирование по поверхностям малого объема, а второй - по

отдельным объемам. Сумма ∑∑П 𝜟𝙎 может быть разбита на две суммы: на сумму выражений П𝜟S по всем поверхностям, отделяющим один объем от сосед­него (по «внутренним» поверхностям), и на сумму П𝜟S по всем «периферийным»поверхностям. Первая сумма равна нулю, так как для двух смежных объемов. внешние нормали к об­щей поверхности направлены встречно. Рис. 22.3 поясняет это; mn — общая грань двух объемов. Для верхнего объема нормаль к грани направлена вниз (𝜟S₁, для нижнего — вверх (𝜟S₂); вектор П, будучи умноженным на (𝜟S₁+ 𝜟S₂),

даст нуль. Сумма П𝜟S по всем периферийным поверхностям и представляет собой ∮ПdS.

Теорему Умова — Пойнтинга для мгновенных значений записывают следующим образом:

 

Напомним вывод этого соотношения. Введем индексы а и b, указывающие, по какой переменной (А или В) производится дифференцирование, и учтем, что можно в циклическом порядке менять множители. Будем иметь:

Левая часть (22.12) представляет собой поток вектора Пойнтинга (направленный внутрь объема) сквозь любую замкнутую поверхность S, ограничивающую некоторый объем 𝙑.

Поясним смысл знака «минус» в левой части формулы (22.12). Элемент поверхности dS в любой ее точке направлен в сторону внешней по отношению к рассматриваемому объему нормали. Вектор Пойнтинга П направлен

.внутрь этого объема. Поскольку угол между П и dS больше 90^е, то скалярное про-
изведение ПdS < 0, a —ПdS> 0. Таким образом, за счет знака «минус»-левая часть
формулы (22.12) — величина положительная.

В соответствии с уравнением Джоуля — Ленца в дифференциалной. форме уЕ² есть энергия, выделяющаяся в виде теплоты в единице объема в единицу времени.

Убедимся, что энергия, передаваемая приемнику в единицу времени, равная UI, действительно канализируется по диэлектрику.

С этой целью подсчитаем поток вектора Пойнтинга через попереч­ное сечение диэлектрика, в.рассматриваемом примере представляющее собой кольцо с внутренним радиусом r₁, и наружным r ₂. Напряжен-

ность магнитного поля в диэлектрике, по за­кону полного тока:

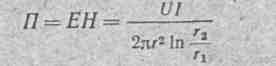
Напряженность электрического поля в ди­электрике при постоянном токе определяется так же, как и в условиях электростатики;

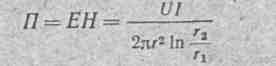
где Q — полный заряд жилы на длине L U-напряжение между жилой и оболочкой. Следовательно, в некоторой точке диэлектрика расположенной на расстоянии r от оси (r₁ r ₂),

 

Обратим внимание также на то, что формула (22.12) учитывает возможность прохождения потока вектора 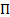транзитом через объем V.

Электромагнитная энергия от места ее генерирования передается к месту потребления по диэлектрику (провода оке в линиях передачи выполняют двоякую роль: они являются каналами; по которым проходит ток, и организаторами структуры поля в диэлектрике).

Покажем справедливость этого утверждения на простейшем при- мере. Пусть энергия постоянного тока передается по коаксиальному кабелю (рис. 22.4), Радиус жилы r₁ внутренний радиус оболочки r₂.Примем проводимость материала жилы и оболочки настолько большой (теоретически бесконечно большой), что напряженности поля Е = /γ в жиле и оболочке стремятся к нулю. Пространство между жилой и оболочкой заполнено диэлектриком.

* Н. А. Умов (1846—1915) с 1893 по 1911 г. являлся профессором Московского университета. В 1874 г. защитил докторскую диссертацию «О движении энергии в уп- ругих средах», где рассмотрен вопрос о потоке энергии в упругих средах и о плотностни потока энергии. Применительно к электромагнитному полю понятие о потоке энергии было развито английским физиком Пойнтингом в 1885 г.

 

Таким образом, вся поступающая к приемнику энергия деистви-

тельно передается по диэлектрику. По жиле и оболочке энергия к приемнику не передается. Более того, если учесть, что γ конечна

_жилы коаксиального кабеля (рис. 22.5), а также подсчитать величи­ну, потока вектора Пойнтинга через боковую поверхность жилы на длине в 1 м и сопоставить величину потока вектора Пойнтинга с потерями энергии в жиле на длине в 1 м. Радиус медной жилы r₁ ==0,3 см;

 

внутренний радиус оболочки г₂ = 1 см. Протекающий по кабелю постоянный ток / = 50 А. Напряжение между жилой и оболочкой U = 10 кВ.

Решение. Нормальная составляющая напряженности элект- рического поля на поверхности жилы:

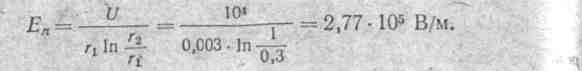
Тангенциальная составляющая напряженности электрического поля на поверхности жилы но закону Ома:

Вектор напряженности электрического поля,Е составляет с нор­малью к поверхности жилы угол α (см. рис. 22.5), тангенс которого:

Напряженность магнитного поля на поверхности жилы, по закону полного тока,

Для определения величины потока вектора Пойнтинга внутрь жилы:
на длине в 1 м следует умножить составляющую вектора Пойнтинга |
Е_tН, проникающую внутрь жилы, на величину боковой поверхности
жилы на длине в 1 м:

Пример 221. На рис. 22.6, а и б изображен сердечник трансформатора и один виток, окружающий сердечник. Концы витка обозначены а и b. Намагничивающая | обмотка трансформатора на рисунке не показана. По сердечнику проходит синусоидально изменяющийся во времени магнитный поток Ф = Ф_m sin ωt. Поток вне сердечника отсутствует. К концам витка а и b присоединим вольтметр электродинамической системы с сопротивлением R_v один раз в соответствии с рис. 22.6, а, другой -по рис. 22.6,6. Определим показание вольтметра в этих двух случаях, полагая, что активное,сопротивление самого витка R_В R_v и что индуктивность рассеяния витка L_S ничтожно мала.

щие от точек а и b витка к вольтметру на рис. 22.6, б, образуют второй виток, в ко-
тором изменяющимся магнитным потокам наводится такая же э. д. с, что и в основ-
ном витке (см. рис. 22.6, в). При обходе контура, состоящего из двух витков, убеж-
даемся, что суммарная э. д. с. в контуре равна нулю. 2. Такой же вывод сделаем,
если учтем, что суммарный поток, пронизывающий заштрихованную площадь кон-
тура. 22.6. в, равен нулю (поток'; '

вне сердечника по условию, отсутвует)

Рассмотренный пример свидетельствует' о том, что при измерениях в переменном электромагнитном поле показание вольтметра зависит от того, как расположены провода от вольтметра, до объекта измерения.

§ 22.7. Теорема Умова —

Пойнтинга в комплексной формезаписи. Перед тем как записать теорему Умова — Пойнтинга в комплексной форме, рассмотрим вопрос о полной мощности в цепи

переменного тока. Полная мощность S = UI = Р + jQ.

Пусть цепь переменного тока содержит последовательно соеди­ненные активные сопротивления R,. индуктивность L и емкость С. Тогда реактивная мощность

где U_c—напряжение на конденсаторе.

Таким образом, реактивная мощность Q равна разности между

магнитной v_м и электрической w_э энергиями цепи, умноженной на 2 .

Подобно тому как в цепи переменного тока для вычисления полной

мощности S надо умножить комплекс напряжения U на сопряженный

комплекс тока I, вводится в употребление комплексный вектор Пойнтинга

 

 

Первое слагаемое правой части (2-2.13) представляет собой активную мощность, второе — реактивную. Таким образом, теорему Умова— Пойнтинга можно записать еще следующим образом:

В таком виде ее часто используют для определения активного и внутреннего реактивного сопротивлений проводников на переменном токе (подробнее см. § 23.7).

§ 22.8. Некоторые замечания к § 22.1. Первое замечание. В уравнения Макс- велла входят параметры ε_а, γ, μ_а, характеризующие усредненные в пространственном и временном смысле свойства вещества. При низких частотах эти параметры представляют собой действительные (некомплексные) числа— такими и будем их считать в курсе ТОЭ. При высоких частотах в диэлектриках существенную роль на­чинают играть диэлектрическая вязкость и другие процессы.