основы магнитной гидродинамики

§ 28.1. Определение магнитной гидродинамики и краткая характеристика об-растей ее применения. Магнитная гидродинамика — это область науки, в которой изучают поведение плазмы пли проводящей жидкости (расплавленных металлов или. солей) в магнитном или электромагнитном полях.

Плазмой называют полностью или частично ионизованный газ, в котором кон­центрация положительных и отрицательных ионов одинакова, а суммарный заряд в единице объема равен нулю. Этот газ в магнитогидродинамическом приближении можно рассматривать как своеобразную проводящую жидкость. При движении (жидкости (плазмы) в магнитном (электромагнитном) поле в ней возникают электрические токи, взаимодействие которых с магнитным полем вызывает механические силы, влияющие на характер ее движения.

За последние 25 лет магнитная гидродинамика особенно интенсивно развивалась в трех направлениях: а) исследование космических проблем; б) изучение способов воздействия на высокотемпературную плазму (ее термоизоляцию, импульсное уско-Ирение, работы по управляемой термоядерной реакции); в) разработка методов элек­тромагнитного воздействия на жидкий металл при его плавке, транспортировке,дозировании.

В космосе имеется полностью ионизованный газ (плазма). Проводимость его в некоторых случаях по порядку величины сможет приближаться к проводимости металла. Если учесть, что ионизованные газы занимают колоссальные объемы, то несмотря на большие расстояния между космическими телами, сопротивления между ними относительно невелики. В то же время магнитное поле в космосе может быть значительньм. Так, регулярное магнитное поле солнца около 25 ^10-4 Т, а в области солнечных пятен достигает 0,2 0,4 Т. Эти магнитные шля создают огромные медленно затухающие токи в плазме, взаимодействие которых с магнитным полем создает механические силы. Даже если эти силы и оказываются небольшими по величине, их влияние на движение плазмы 'значительно, так как они воздействуют на нее в течение длительного времени.

Различают высокотемпературную и низкотемпературную плазмы. По степени концентрации^; заряженных частиц плазму различают на разреженную и плазму с большой концентрацией. У высокотемпературной плазмы температура доходит до нескольких миллионов градусов. Низкотемпературная плазма имеет место, например, в столбе ионизованного газа при тлеющем и дуговом разрядах. Плазма с тем-ВЮературой нескольких тысяч градусов образуется, например, вблизи поверхности ракеты при ее вхождении в плотные слои атмосферы.

Магнитная гидродинамика наряду с другими науками является теоретической основой при разработке магнитогидродинамических генераторов, а также плазмен-

ных и ионных двигателей.

Применение жидкометаллических теплоносителей в паровых машинах и турби-

нах, охлаждение атомных реакторов щелочными металлами, натрием и калием,

 

разлив и транспортировка жидкого металла в металлургии— все это вызвало по- требность, в магнитных насосах, вентилях, дозаторах.

При исследовании поведения проводящей жидкости в магнитном поле свойства ее характеризуют проводимостью у и магнитной проницаемостью μ_а. Значения γ и μ_a полагают известными из молекулярно-кинетической теории. Точно так же, когда изучают поведение плазмы в магнитном поле, значения γ и μ_а для нее считают известными из электронной теории. Обычно полагают, что среда является однородной и изотропной и что ее свойства не зависят от температуры. Однако при определенных условиях γ плазмы может, оказаться величиной тензорной, например γ плазмы в области солнечной короны.. Иногда необходимо рассматривать плазму как двухком- понентную (не однокомпонентную) среду.

§ 28.2. Уравнения магнитной гидродинамики. Систему уравнений магнитной гидродинамики образуют следующие группы уравнений.

Уравнения Максвелла применительно к движущейся проводящей среде. Прово­дящая среда по отношению к некоторой системе отсчета движется со скоростью v во внешнем магнитном поле индукции В. Скорость движения среды ничтожно мала по сравнению со скоростью света, поэтому релятивистские поправки в уравнения, Максвелла не вносят. Ток смещения не учитывают, так как он ничтожно мал по -. сравнению с током проводимости.

Напряженность электрического поля равна сумме электрической и магнитной

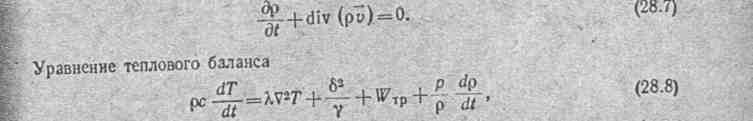
составляющих Е+ [vВ]. Тогда

Уравнение-Навье—Стокса выражает собой второй закон Ньютона применительно к единице объема проводящей среды, движущейся в магнитном поле.

Произведение массы единицы объема ρ, движущейся со скоростью v жидкости на ускорение равно сумме сил, действующих на единицу объема:

Где полная или материальная производная, учитывающая изменение v в данной точке во времени и в результате того, что точка наблюдения попадает в поле

 

с иными значениями v вследствие движения; F₁ = —grad p — сила, вызванная перепадом давления и направленная в сторону уменьшения давления (тогда как grad р направлен в сторону увеличения давления); F₂ = pg — сила тяжести, действующая на единицу объема; (g— ускорение силы тяжести в данной точке); F₃ — сила вязкого трения на единицу объема; v — кинематический коэффи­циент вязкости.

Сила вязкого трения взята пропорциональной второй производной скорости потому, что равна разности сил, действующих с каждых двух противоположных граней объема, отнесенной к расстоянию между гранями; F₄ = [δВ]—-электромаг­нитная сила. Выражение для нее получим из формулы (21.1), если ввести ток I в квадратные скобки и заменить произведением плотности тока δ на сечение , через которое он проходит; затем обе части выражения F = [ l B] разделить на выделенный объем проводящего тела l = l .

Уравнение непрерывности, выражающее собой то обстоятельство, что изменение массы в элементарном объеме обусловлено притоком жидкости (плазмы),

Силы F₂ и F₃ малы по сравнению с F₁ и F₄ и поэтому их не учитывают. Окончательно имеем:

 

Где ρс тепло расходуемое на увеличение температуры объема; с —удельная теплоемкость; λ ²T — тепло, приносимое в единичный объем за счет теплопровод­ности; λ — коэффициент теплопроводности; δ²/γ— джоулевы потери в единице объема; W_тр — тепло, выделяющееся в объеме в силу наличия трения; р — давление; ρ /р dp/ dt— тепло при изменении плотности р. В установившемся тепловом режиме температура Т неизменна и в этом случае уравнение (28.8) не используется.

§ 28.3. Просачивание (диффузия) магнитного поля. Положим, что плазма неподвижна. Из уравнений (28.5) и (28.6) при v= 0 следует:

 

 

Уравнение (28.9) является уравнением диффузии или уравнением теплопроводности где 1/γμ_а коэффициент диффузии. Если принять, что В имеет только одну
не равную нулю составляющую в декартовой системе координат В = iB_x (х, t), то
Решение (28.9) будет следующим:

где v - параметр; a (v) и b (v) - постоянные интегрирования, определяемые из начальных и граничных условий.

 

Из (28.11) следует, что поле, просачиваясь сквозь плазму, затухает с постоян- ной времени:

τ=γμ_а l ² (28.12)

где l — линейный размер области, занятой полем.

На расстоянии l укладывается одно колебание sin vx или cos vх при v = 1.

§ 28.4. Электромагнитный барьер. Согласно уравнению (28.10) grad р перпендикулярен плоскости, в которой расположены векторы δ и В (рис. 28.1). Отсюда следует, что при определенной конфигурации поля давление р может быть уравно­вешено электромагнитной силой. Это особенно важно хотя бы для кратковременной локализации плазмы с температурой порядка миллиона градусов, когда не при­ходится рассчитывать на барьеры из какого-либо вещества.

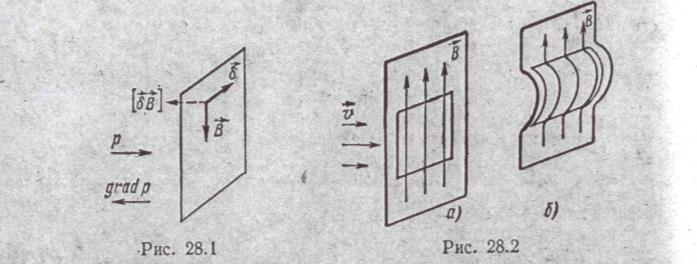
§ 28.5. Вмороженное поле. Положим, что проводимость плазмы γ очень велика, теоретически стремится к бесконечности и что плазма находится в движении со ско­ростью v. На рис. 28.2, а показана плоскость, в которой в исходном состоянии рас­положены линии магнитной индукции. Возьмем произвольный контур в этой пло­скости и допустим, что скорость движения плазмы поперек линий В стала неодина­ковой (см. стрелки для v на рис. 28.2, а). Через некоторое время плоскость дефор­мируется и примет вид, изображенный на рис. 28.2, б. Силовые линии растянутся вместе с контуром, они как бы приклеены или вморожены в плазму (поток через кон­тур останется неизменившимся). Физически это объясняется тем, [что при движе­нии плазмы поперек линий В в ней индуктируются токи, поле которых, складываясь с первоначальным, так его деформирует, что силовые линии смещаются вместе с плаз­мой. Практически проводимость v не бесконечно велика и поэтому деформация линий В несколько отстает от деформации контура.

§ 28.6. Возникновение волн в плазме. При определенных условиях в плазме могут возникать магнитогидродинамические волны. Для выяснения механизма их возникновения обратимся к рис. 28.3. Для упрощения выкладок примем, что про­водимость плазмы γ .

Прямоугольная система координат расположена в плазме так, что внешнее магнитное поле индукции В₀ направлено по оси z. Положим, что по какой-то при­чине слой плазмы / (рис. 28.3, б) начал двигаться со скоростью v в направлении оси у. Так как движение этого слоя есть движение проводящего тела в магнитном поле, то в каждой точке слоя 1 возникнет напряженность поля [vB] = i v B₀. Под ее действием в плазме возникнут токи проводимости с плотностью δ= 1/μ_а rot B

замыкающиеся через соседние слои, как показано на рис. 28.3, о. Результирующая индукция В равна сумме индукции внешнего поля В₀ и индукции b от токов проводимости: В =jb+kB₀.

 

Сила F1 действующая на слой плазмы1,начавший двигаться первым,будет замедлять его движение.Слои 2 и 3,расположенные выше и ниже слоя 1 (в них токи направлены в противоположную сторону по сравнению с током в слое 1),будут испытывать силы F₂ и F₃,под воздействием которых слои начнут двигаться по оси y,

 

Вдоль направления внешнего магнитного поля возникают две волны, распростра­няющиеся со скоростью v₁ = ± kv_1. Одна из них распространяется вверх, другая — вниз. Волны будут поперечными — слои плазмы движутся перпендикулярно направ­лению распространения волны. Рассмотренный тип волн называют волнами Альфена.

Давление р волны изменяется только в направлении оси z:

Если учесть, что γ конечна, не бесконечно велика, то вследствие потерь от вихре­вых токов и от вязкого трения амплитуда волны А по мере продвижения волны вдоль оси z будет затухать по экспоненте.

В плазме могут возникать и другие типы волн, при которых силовые линии, увлекаемые частицами плазмы или жидкости, участвуют в турбулентном движении.

§ 28.7. Эффект сжатия (пинч-эффект). В цилиндрическом столбе электрической дуги (рис. 28.4) нити тока параллельны'. Каждый элемент этой нити находится в маг-

 

(рис. 28.6, а). В перпендикулярном направлении создают сильное магнитное поле
индукции В. На ионы плазмы воздействует лоренцова сила Ё = [vB]. Под ее дей­-
ствием положительные заряды движутся по направлению Е к электроду 1, а отри-­
цательные заряды — встречно Е к электроду 2. Между электродами возникает раз-­
ность потенциалов, равная Eh. Если электроды замкнуть на сопротивление R, то по
замкнутому контуру потечет ток, а плазма будет испытывать тормозящее воздействие.
§ 28.10. Принцип работы плазменного реактивного двигателя. Сгустки плазмы
вдуваются в полость между проводящей трубкой и проводником, расположенным
на оси трубки (рис. 28.6, б). Плазма замыкает собой трубку и осевой проводник.
Ток, протекающий по трубке, плазме и осевому проводнику, создает магнитное поле,
которое выдувает плазму вправо. Плазма, получив ускорение, с силой выбрасывается из трубки в вакуум вправо, а трубка получает импульс движения влево.

 

нитном.поле индукции В, направленной по касательной к нити тока. На каждый элемент тока с плотностью δ действует сила. F= [δSJ. Под действием этих сил нити тока стремятся сжаться, а столб дуги уплотниться. Но температура газа (плазмы,) а следовательно, и давление будут максимальны на оси. Силе сжатия противостоит давление. Система находится в равновесии, когда электромагнитная сила сжатия уравновешена силой давления.

§ 28.8. Принцип работы магнитного насоса и маг­нитного вентиля. В магнитном насосе механическое воз­действие на проводящую жидкость создается магнитным полем. Принцип работы насоса кондукционного типа пояс­няет рис 28.5..Участок трубопровода находится в скре-

щенных магнитном и электрическом полях; Магнитное поле направлено сверху вниз, электрическое — от точки т. к точке n. Под действием электрического поля в напра-. влении от т к п через жидкость течет ток. На каждый элемент объема жидкости с плотностью тока δ действует сила F.= [δB], направленная согласно с направлением движения жидкости по трубопроводу, т.е. устройство действует как насос.

Если при прочих равных условиях изменить направление электрического или магнитного поля, то возникнет сила, препятствующая движению. В этом случае устройство будет работать в качестве тормоза или вентиля. Управлять величиной силы можно, изменяя величину В.

§ 28.9. Принцип работы магнитного гидродинамического генератора. Через канал с большой скоростью v продувают плазму, нагретую до высокой температуры

ПРИЛОЖЕНИЯ К ЧАСТИ III

ПРИЛОЖЕНИЕ Е'

РАСЧЕТ ПОЛЕЙ ПО МЕТОДХ СЕТОК

И МОДЕЛИРОВАНИЕ ПОЛЕЙ ПО МЕТОДУ

ЭЛЕКТРИЧЕСКИХ СЕТОК

Довольно широко, распространены: а) числовой расчет электрических и маг­нитных полей' по методу сеток; б) моделирование электрических и неэлектрических (магнитных) полей по методу электрических сеток. Несмотря на близость названий, содержание методов существенно различно.

_ § Е .1. Расчет полей по методу сеток. Метод сеток представляет собой число­вой метод интегрирования дифференциальных уравнений в частных производных путем сведения их к уравнениям в конечных разностях.

На рис. Е'1, а изображен участок двухмерного поля. На нем показаны оси х и у декартовой системы и квадратная сетка со стороной b. Точки (узлы) сетки обозна­чены цифрами 0, 1, 2, 3, 4. Примем φ₀ — потенциал точки 0, φ₁ — потенциал точки 1 и т. д. Выведем приближенное соотношение между потенциалами φ₀ φ_4,вытекающее из уравнения Пуассона. Среднее значение первой производной ∂φ/∂х на участке

 

Уравнения (Е',1) и (Е'.2) определяют связь между потенциалами квадратной сетки. Они являются основными в методе сеток. Чем меньше шаг сетки b, тем меньше погрешность от замены уравнений Пуассона или Лапласа соответственно на уравне­ния (E'.l) или (Е',2). При расчете по методу сеток применяют не только квадратные, но и иные сетки, например полярные. Для них имеются формулы в конечных раз­ностях, в общем случае отличные от формул (E'.l) и (Е'.2).

Допустим, что двухмерное поле, подчиняющееся уравнению Лапласа, ограничено некоторыми поверхностями и известны потенциалы этих поверхностей (задача Дирихле), либо известны значения производной от потенциала по нормали к каж­дой граничной поверхности во всех точках (задача Неймана). Возможны и комбиниро­ванные типы задач, когда для одной части граничных поверхностей известны зна­чения потенциалов, а для другой — значения нормальной производной от потен­циала.

Требуется найти значения потенциалов прямоугольной сетки этого поля. Пос­ледовательность расчета для задачи Дирихле проиллюстрируем на примере расчета поля, образованного двумя параллельными прямыми углами рис. Е'1,-б. В месте поворота расстояние между параллельными сторонами угла изменяется. Потенциал верхней границы положим равным 75 единицам, нижней — нулю. Будем полагать, что

объемные заряды отсутствуют.

1. Тонкими сплошными линиями нанесем квадратную сетку. Обозначим узлы получившихся квадратов буквами а, б, в, г, д,... (расположены в кружках).

2. Произвольно выберем значения потенциалов узлов а, б, в,... Объем дальней­шей вычислительной работы в значительной мере зависит от того, насколько близко к действительному выбрано первоначальное распределение потенциала. Поэтому следует стремиться к возможно более правдоподобному первоначальному распреде­лению потенциала.

Для этой цели нанесем на рис. E'.l приближенную картину силовых и экви­потенциальных линий и, руководствуясь ею, запишем начальные значения потен­циалов узлов (цифры слева и вверху у каждого узла).

7* 203

узла находим величину остатка в формуле (Е'.2). Так, остаток для точки б равен 53+ 50+75+ 25- 4 50 = 3. Записываем величину остатка в правом верхнем углу у каждого узла.

4. Поскольку в каждом узле остаток должен быть равен нулю, то дальнейший и наиболее трудоемкий этап расчета состоит в таком изменении потенциалов узлов, чтобы остатки во всех узлах не превышали некоторой заданной величины (скажем, 1 или 2).

Поэтому в одной из точек с наибольшим значением остатка изменяем потенциал приблизительно на ¹/₄ от остатка (в рассматриваемом случае в точке б уменьшаем потенциал на единицу) и затем пересчитываем остатки во всех остальных узлах. Вновь полученные остатки записываем в левом нижнем углу у каждого узла (на рисунке они выписаны не для всех узлов). Такая операция выполняется несколько раз до тех пор, пока все остатки не станут равны или меньше заданной величины. Процесс является сходящимся. При расчетах используют счетные машины.

Метод применим для магнитных и электрических полей, линейных и нелинейных сред, для неизменных и изменяющихся во времени полей.

§ Е'.2. Моделирование полей по методу электрических сеток. Моделирование полей с помощью электрических сеток представляет собой метод экспериментального исследования полей, подчиняющихся уравнению Пуассона, путем измерения потен­циалов узлов электрической сетки, которой заменяется сплошная среда. Положим, что. требуется выяснить распределение потенциалов в некоторой области (сплошной среде), потенциалы границ которой заданы. Кроме того, известны электрическая или соответственно магнитная проницаемость среды, а также плотность распределенных источников в исследуемом поле (например, плотность свободных зарядов р_своб в моде­лируемом электростатическом поле).

Исследуемое поле заменим полем в проводящей среде, с проводимостью γ. Моде­лируемую область разделим на элементарные объемы, например на кубы. Каж­дый элементарный объем заменим электрической схемой замещения в соответствии с рис. Е'1, в.

Пусть ребро куба имеет длину 2а. Центр куба обозначим цифрой 0, а точки,

лежащие в серединах его граней, — цифрами 1—6. Шаг сетки в направлении осей

х, у, z обозначим х, у, z ( х = у = z = а). Проводимость между любой

 

из точек 1-6 и центральной точкой 0 g = γ = 4γа.

К узлу 0 от источника тока подтекает ток I₀ = 2δ (х, у, z) а³. К остальным узлам, не показанным на рис. E'.l, в, подтекают своп токи. Эти токи, подводимые в центры кубов, выполняют функции распределенных источников в исходном поле. Значения токов определяются по заданной плотности распределенных источников. По первому закону Кирхгофа, сумма токов, подтекающих к узлу 0, должна быть равна нулю, т. е.

Проделав аналогичные выкладки с остальными слагаемыми уравнения (Е.З), подставив в него выражение для I₀ и сократив на 4а³, получим уравнение Пуассона

Таким образом, распределение потенциалов в электрической сетке с точностью до частных производных четвертого порядка от φ, умноженных на а²/ 4!, удовлетво­ряет тому же уравнению что и распределение потенциалов в сплошной среде.

Распределение, потенциалов в узлах 0 элементарных объемов измеряется ком­пенсационным способом.

Моделирование позволяет на относительно дешевой модели исследовать поля, с трудом или совсем не поддающиеся аналитическому расчету.

приложение ж

МЕТОД ГРИНА

§ Ж. 1. Формулы Грина. Формулы Грина получают из теоремы Остроград­ского — Гavcca

где D_n — нормальная составляющая некоторого вектора D на поверхности S, огра-­
ничивающей объем V; D_n направлена в сторону внешней нормали п по отношению
к объему V.

Положим, D = αF, где α — произвольный скаляр, а вектор F представим как градиент некоторой скалярной функции,φ: F=grad φ. Тогда

divD = div (α grad φ)= (α ) = α ² φ+

Подстановка в (Ж.1) дает:

§ Ж.2. Гармонические функции. Гармонической называют функцию, непрерыв­ную в рассматриваемой области вместе со своими производными до второго порядка включительно и удовлетворяющую уравнению Лапласа в этой области. Центрально симметричная функция 1/r, где r — расстояние от некоторой фиксированной точки объема (например, от точки А рис. Ж.1,а) до текущей точки В, является гармони­ческой функцией. Для плоскопараллельного поля гармоническая функция равна In r. Примем в формуле (Ж.3). что α и φ — гармонические функции, α = 1/r и функция φ

выполняет роль потенциала φ. Тогда ² φ= 0, ² α= 0 для поверхности, ограни­чивающей область V, имеет место соотношение

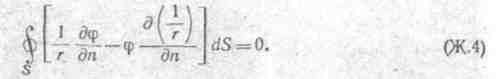
§ Ж.З. Интеграл Грина для гармонических функций. Применим формулу (Ж.4) для определения потенциала в произвольной точке В объема V. С этой целью окружим точку В сферой S_B малого радиуса р (рис. Ж.1, б) и применим формулу (Ж.4) к по­верхностям S и S_В

Он определяется значением потенциала и нормальной Производной потенциала на поверхности, ограничивающей область V. Физически первое слагаемое фор-

мулы (Ж.5) обусловлено поверхностными зарядами, как бы вкрапленными в поверх­ность S, а второе — зарядами диполей на поверхности, т. е. двойным заряженным слоем.

§ Ж.4. Функция Грина. Положим, что в точке А рис. Ж.1, в находится точеч­ный заряд q = 4πε_а, а поверхность S является проводящей и заземлена, т. е. потен­циал ее равен нулю. Вследствие электростатической индукции на внутренней стороне поверхности возникают отрицательные наведенные заряды плотностью —σ, а на на­ружной +σ. Суммарный отрицательный заряд на внутренней поверхности равен сум­марному положительному заряду на внешней поверхности и каждый из них численно равен q.

Обозначим расстояние произвольной точки В до точки А через r, а до произ­вольной точки на поверхности — через R. Тогда

Если точка В будет находиться на поверхности S, то ее потенциал по условию задачи должен быть равен нулю.

Функцией Грина G = + g называют функцию, которая обладает свойством потенциала произвольной точки В в рассматриваемой задаче, т..е. она является гармонической функцией и принимает нулевое значение на поверхности S. Функ­ция G определена через функцию g, которая представляет собой решение уравнения Лапласа для рассматриваемой задачи. Основная трудность решения методом функ­ций Грина заключается в отыскании функции g. Она найдена лишь для некоторых частных случаев: например, в поле точечного заряда q = 4πε_а, расположенного на расстоянии h от проводящей плоскости (рис. Ж.1, в G = - _'

§ Ж.5. Определение потенциала φ через функцию Грина в общем случае. В объ­еме V, ограниченном поверхностью S, имеются объемные заряды ρ, распределенные с заданной плотностью, известны потенциалы поверхностей и функция Грина. Положим в формуле (Ж.4) α= g = G – 1/ r, учтем, что ²α = 0, а ²φ = — ρ/ε_а. Тогда

Кроме того, из физических соображений следует, что потенциал произволь­ной точки В определяется объемными и поверхностными зарядами, а также двойным заряженным слоем (диполями) на границе :

Вычтем (Ж.6) из (Ж.7), учтем, что функция Грина на поверхности S равна нулю. Получим формулу для определения потенциала произвольной точки φ_в через функ­цию Грина и ее нормальную производную:

 

где n – внешняя нормаль к объему. Примеры на применение формулы (Ж.8) см.в (9)

МЕТОД ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ

Метод интегральных уравнений (ИУ) представляет собой метод расчета маг­нитных и электрических полей, основанный на введении вторичных источников и состоящий в сведении задачи к интегральным уравнениям, и их числового решения на ЭВМ. В настоящее время его применяют главным образом для решения двух­мерных задач, но с увеличением объема памяти ЭВМ он может быть применен и к трех­мерным полям.

Имеется два варианта: метода интегральных уравнений, отличающихся, видом вторичных источников. Идея метода и его первый вариант предложены Г. А. Грин­бергом [6]. Дальнейшее развитие метода и, доведение его до практических расчетов осуществлено О. В. Тозони [15], Э. В. Колесниковым, И. Д. Маергоиз и др. Раз­работка второго варианта метода осуществлена О. В. Тозони [16] й др. ''

§ 3.1. Первый вариант метода интегральных уравнений. Идею метода рассмо-­
трим применительно к магнитному полю, образованному намагничивающими обмот­-
ками, геометрия и ток в которых известны, и намагниченными ферромагнитными
телами. Однородно намагниченные ферромагнитные тела в расчетном смысле можно заменить вакуумом (воздухом), поместив на поверхность ферромагнитных тел поверх­-
ностные токи с плотностью σ на_единицу длины (пояснения о поверхностных токах
см. в §14.24, где они были обозначены δ_м). Значение а в различных точках поверхности
неизвестно и подлежит определению. Значение плотности тока проводимости δ
в обмотках известно.

Рассмотрим условия на границе между ферромагнитным телом (среда е) и воз­духом (среда i) — рис. 3.1, а. На рис. 3.1, б показана та же граница, что и на рис. 3.1, а, но ферромагнитное (ф.м.) тело заменено воздухом, а на границе помещен поверхностный ток с плотностью σ на единицу длины.

Тангенциальные (о чем свидетельствует индекс t) составляющие напряженности поля на границе Нⁱ _t р среде i и Н ^е_tв среде е состоят каждая из двух компонент: из составляющей H'_t, обусловленной всеми токами проводимости, протекающими по обмоткам электрического аппарата, и всеми поверхностными токами (их называют связанными токами) на границе ферромагнитной области, кроме поверхностного тока σdl, протекающего по рассматриваемому элементу поверхности, и из составляющей H^" _t ., обусловленной поверхностным током σdl в рассматриваемом элементе поверх­ности ферромагнитного тела (выбран направленным к читателю).. Тангенциальные составляющие индукции на границе:

Применим закон полного тока к пунктирному контуру на рис. 3.1, б, охва­тывающему кусочек границы длиной dl Получим

 

 

Применим закон полного тока к пунктирному контуру на рис. 3.1, б, охва­тывающему кусочек границы длиной dl Получим

2Н"_{t = σ} (3.3)

При составлении циркуляции по этому контуру учли, что по верхней и по ниж­-
ней границам контура составляющих Н'_tв соответствии с рис. 3.1, б нет. Так как
тангенциальные составляющие напряженности поля на границе воздух — ферро­-
магнитное тело равны, то

 

где А — значение вектора потенциала в произвольной точке наблюдения Q, рас­положенной на контуре ферромагнитного тела L; N — произвольная точка сечения, обмотки с током, плотность тока в которой δ (N); r _QN — расстояние от точки Q до точки N (рис. 3.1, в); М — произвольная точка на контуре L с плотностью поверх­ностного тока σ (М).

Обход контура выберем против часовой стрелки, а нормаль n направим во внеш-

нюю область по отношению к контуру L. Тогда В'_t = — . Так как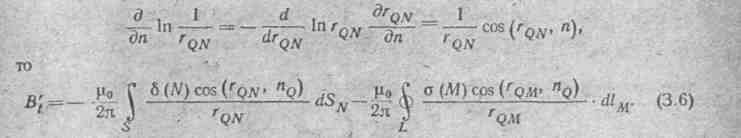

Подставив формулу (3.6) в (3.5), получим интегральное уравнение второго рода Фредгольма относительно плотности поверхностного тока на контуре L фер­ромагнитного тела:

Для каждой точки Q контура L функцию F (Q) можно подсчитать заранее [до решения уравнения (3.7)], так как распределение тока проводимости δ (N) и гео­метрия магнитной системы известны. Если контуров, ограничивающих ферромаг­нитную область, несколько (т. е. область многосвязна) — например, на рис. 3.1, г область ограничивают два контура £._х и L₂ —то уравнение (3.7) заменяют системой уравнений (число уравнений равно числу контуров). В каждое уравнение входят слагаемые от поверхностных токов и в других контурах (а не только от поверхност­ных токов в своем контуре).

Уравнение типа (3.7) решают на ЭВМ итерационным методом, заменяя интегралы конечными суммами. Чтобы итерационный процесс сходился, используют интеграль­ные соотношения для контуров L, вытекающие.из закона полного тока. После, на­хождения σ (Q) определяют B'_t, а по ним и по А — любую точечную или интеграль­ную характеристику поля.

Подробное рассмотрение первого варианта метода, составление программ для ЭВМ, числовые примеры и распространение метода на нелинейные магнитные системы -читатель найдет в [15], О применении метода к электростатическим полям см. [9].

§ 3.2. Второй вариант метода интегральных уравнений. Первый вариант ме­тода ИУ имеет тот недостаток, что если параметра в уравнении (3.7) окажется близок к 1, то малая погрешность, допущенная при подсчете F (Q) по формуле (3.8), приведет к большой погрешности при определении закона распределения ст. Чтобы этого недостатка избежать, в [16] описан второй вариант метода ИУ с иными вторич­ными источниками. Рассмотрим основы второго варианта. С этой целью запишем систему уравнений Максвелла сначала через векторы В и Е, а затем через векторы D и Н, полагая, что е и ц являются функциями координат.

Первое уравнение Максвелла:

 

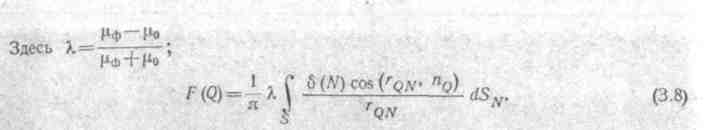
Система (3.14 3.16) свидетельствует о том, что поле векторов D и Н в ва­кууме создается системой первичных источников — плотностей токов проводи­мости δ объемных зарядов ρ и системой вторичных источников — плотностями фиктивных магнитных токов:

 

Если расчет магнитного поля постоянного тока в кусочно-неоднородной среде вести с использованием вторичных источников второго типа, т.е. фиктивных маг­нитных зарядов р_m (Q, t) и поверхностной плотности токов на поверхностях фер­ромагнитных тел ∂_m (Q, ), то, выразив Н (Q, t) через первичные и вторичные источ­ники и подставив ее в формулы

 

 

где S_ф, — поверхность; V_ф — объем ферромагнетика; D — объем, занятый токами проводимости δ; n_q — единичная нормаль к поверхности в точке Q.

Систему уравнений (3.21—3.22) решают совместно с уравнением (3.19) либо прямым, либо итерационным методом. Методику решения и программы для ЭВМ см. в [16].

приложение и

МЕТОД КОНФОРМНЫХ ПРЕОБРАЗОВАНИЙ (ОТОБРАЖЕНИИ)

Метод конформных преобразований — это метод анализа и расчета неизменных во времени двухмерных электрических и магнитных полей, удовлетворяющих урав­нению Лапласа, основу которого составляет конформное преобразование совокуп­ности точек одной плоскости комплексного переменного в совокупность точек другой плоскости.

§ И.1. Комплексный потенциал. Расположим оси декартовой системы в иссле­дуемом поле так, что ось zбудет перпендикулярна полю. Плоскость хоy будем назы­вать плоскостью z. Каждая точка поля имеет некоторые координаты х и y. Плоскость хоу можно считать комплексной плоскостью. Тогда положение точки на плоскости будет характеризоваться комплексным числом z = х -f- jy.

совокупность точек х, у, принадлежащих эквипотенциальной линии, обозначим U (х, у) = U, а совокупность точек, принадлежащих силовой линии, назовем V (х, у) — V. Из § 19.5 известно, что в