Абсолютно конвергентна, т.е. сумма абсолютных значений имеет предел.

7. Для всех u P и t T, ,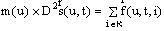

где D² - вторая производная 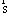; это хорошо известное уравнение: масса ускорение = сила.

По Сниду и Штегмюллеру, это чисто теоретико-множественное определение позволяет сделать эмпирическое утверждение: данная структура имеет некоторое применение a к реальным системам. Например, в виде такой структуры можно представить солнечную систему. Такого рода эмпирические утверждения могут выражаться следующим образом: a имеет структуру, определяемую специальной теорией, сокращенно: a имеет s, где под s понимается фундаментальный закон данной теории (например, КМЧ).

Затем Снид и Штегмюллер определяют понятие " теоретической величины " как величины, полученной при помощи теоретически зависимого измерения. Это значит, что определение величины зависит от предшествующего успешного применения именно тех теорий, в которых эта величина фигурирует. Например, сила и масса - теоретические величины в КМЧ, а положение частицы и время - не являются таковыми, поскольку они могут быть измерены немеханическим способом, скажем, оптическим.

Всякое применение теории a называется моделью S и отличается от возможной (потенциальной) частной модели КМЧ. Например, кинематика частицы (КЧ) - возможная частная модель КМЧ. В соответствии с предыдущим определением:

КЧ (x) существуют множества P,T и функция 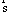, удовлетворяющая условиям 1-4. Здесь уже не фигурируют масса и сила (то же самое относится к пункту 1, где также фигурировали эти функции). Таким образом, КМЧ предстает как "теоретическое расширение" КЧ. Тогда вместо того, чтобы говорить: " a имеет S", можно сказать иначе:

(1) a - возможная частная модель S, и существует теоретическое расширение, обозначаемое x, являющееся моделью S. Это так называемая "примитивная форма Рамсея, выражающая эмпирическое содержание теории".

Но зачем нужна усложненная формулировка (1) вместо более простой " a есть S"? Снид и Штегмюллер объясняют это так: чтобы проверить " a есть S", необходимо определить значения некоторых теоретических величин. Но по определению для этого нужны успешные применения теории, обладающей структурой S. А чтобы проверить эти применения, надо предположить другие, более ранние применения, и т.д. В результате получается регресс в бесконечность или логический круг. Чтобы избежать этого и выявить эмпирическую истинность (1), утверждают Снид и Штегмюллер, достаточно знать, удовлетворяют ли этой формулировке те величины, которые фигурируют в a. Например, в рамках КЧ и/или КМЧ подтверждение (1) должно основываться на доказательстве той гипотезы, что для некоторых частиц интервал времени и вектор их положения соответствуют друг другу. В таком случае возможно такое теоретическое расширение, которое является моделью КМЧ, другими словами, теоретические функции КМЧ могут быть применены к такой системе a, которая станет возможной частной моделью КМЧ. Таким образом, по сравнению с выражением " a есть S" (1) представляет собой более слабое эмпирическое утверждение, то есть утверждение о лишь возможном, а не об актуальном применении теоретически зависимых величин.