Смысл статистических методов контроля качества заключается в значительном снижении затрат на его проведение по сравнению c органолептическими (визуальными, слуховыми и т.п.) со сплошным контролем, с одной стороны, и в исключении случайных изменений качества продукции – с другой.
Различаются две области применения статистических методов в производстве (рис. 4):
- при регулировании хода технологического процесса с целью удержания его в заданных рамках (левая часть схемы);
- при приемке изготовленной продукции (правая часть схемы).
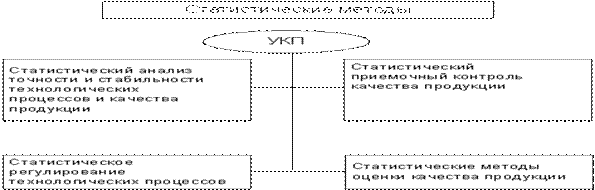
Рис. 4. Области применения статистических методов управления качеством продукции
Для контроля технологических процессов решаются задачи статистического анализа точности и стабильности технологических процессов и их статистического регулирования. При этом за эталон принимаются допуски на контролируемые параметры, заданные в технологической документации, и задача заключается в жёстком удержании этих параметров в установленных пределах. Может быть поставлена также задача поиска новых режимов выполнения операций с целью повышения качества конечного производства.
Прежде чем браться за применение статистических методов в производственном процессе, необходимо четко представлять цель применения этих методов и выгоду производства от их применения. Очень редко данные используются для заключения о качестве в том виде, в каком они были получены. Обычно для анализа данных используются семь, так называемых, статистических методов или инструментов контроля качества.
1. Расслаивание (стратефикация).
При разделении данных на группы в соответствии с их особенностями группы именуют слоями (стратами), а сам процесс разделения – расслаиванием (стратификацией). Желательно, чтобы различия внутри слоя были как можно меньше, а между слоями – как можно больше.
|
|
В результатах измерений всегда есть больший или меньший разброс параметров. Если осуществлять стратификацию по факторам, порождающим этот разброс, легко выявить главную причину его появления, уменьшить его и добиться повышения качества продукции.
Применение различных способов расслаивания зависит от конкретных задач. В производстве часто используется способ, называемый 4М, учитывающий факторы, зависящие от: человека (man); машины (machine); материала (material); метода (method).
То есть расслаивание можно осуществить так:
- по исполнителям (по полу, стажу работы, квалификации и т.д.);
- по машинам и оборудованию (по новому или старому, марке, типу и т.д.);
- по материалу (по месту производства, партии, виду, качеству сырья и т.д.);
- по способу производства (по температуре, технологическому приему и т.д.).
Метод расслаивания в чистом виде применяется при расчете стоимости изделия, когда требуется оценка прямых и косвенных расходов отдельно по изделиям и партиям, при оценке прибыли от продажи изделий отдельно по клиентам и по изделиям и т.д. Расслаивание также используется в случае применения других статистических методов: при построении причинно-следственных диаграмм, диаграмм Парето, гистограмм и контрольных карт.
2. Графическое представление данных широко применяется в производственной практике для наглядности и облегчения понимания смысла данных. Различают следующие виды графиков:
|
|
А). График, представляющий собой ломанную линию (рис. 5), применяется, например, для выражения изменения каких-либо данных с течением времени.
Рис. 5.Пример «ломаного» графика и его аппроксимации
Б) Круговой и ленточный графики (рис. 6 и 7) применяются для выражения процентного соотношения рассматриваемых данных.
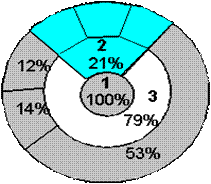
Рис. 6. Пример кругового графика
Соотношение составляющих себестоимости производства:
1 – себестоимость производства продукции в целом;
2– косвенные расходы;
3 – прямые расходы и т.д.
Рис. 7. Пример ленточного графика
На рисунке 7 показано соотношение сумм выручки от продажи по отдельным видам изделий (A,B,C), видна тенденция: изделие B перспективно, а A и C – нет.
В). Z-образный график (рис. 8) применяется для выражения условий достижений данных значений. Например, для оценки общей тенденции при регистрации по месяцам фактических данных (объём сбыта, объём производства и т.д.)
График строится следующим образом:
1) откладываются значения параметра (например, объём сбыта) по месяцам (за период одного года) с января по декабрь и соединяются отрезками прямой (ломаная линия 1 на рис. 9);
2) вычисляется кумулятивная сумма за каждый месяц и строится соответствующий график (ломаная линия 2 на рис. 8);
3) вычисляются итоговые значения (меняющийся итог) и строится соответствующий график. За меняющийся итог в данном случае принимается итог за год, предшествующий данному месяцу (ломаная линия 3 на рис. 8).
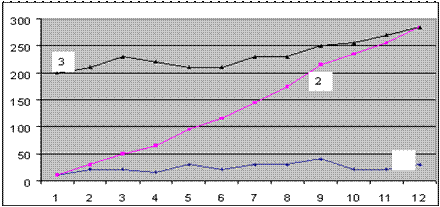
Рис. 8. Пример Z-образного графика.
Ось ординат – выручка по месяцам, ось абсцисс – месяцы года.
По меняющемуся итогу можно определить тенденцию изменения за длительный период. Вместо меняющегося итога можно наносить на график планируемые значения и проверять условия их достижения.
|
|
Г). Столбчатый график (рис. 9) представляет количественную зависимость, выражаемую высотой столбика, таких факторов, как себестоимость изделия от его вида, сумма потерь в результате брака от процесса и т.д. Разновидности столбчатого графика – гистограмма и диаграмма Парето. При построении графика по оси ординат откладывают количество факторов, влияющих на изучаемый процесс (в данном случае изучение стимулов к покупке изделий). По оси абсцисс – факторы, каждому из которых соответствует высота столбика, зависящая от числа (частоты) проявления данного фактора.
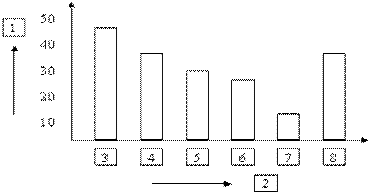
Рис. 9. Пример столбчатого графика.
1 – число стимулов к покупке; 2 – стимулы к покупке;
3 – качество; 4 – снижение цены;
5 – гарантийные сроки; 6 – дизайн; 7 –доставка; 8 – прочие;
Если упорядочить стимулы к покупке по частоте их проявления и построить кумулятивную сумму, то получим диаграмму Парето.
3. Диаграмма Парето.
Схема, построенная на основе группирования по дискретным признакам, ранжированная в порядке убывания (например, по частоте появления) и показывающая кумулятивную (накопленную) частоту, называется диаграммой Парето (рис. 10). Парето – итальянский экономист и социолог, использовавший свою диаграмму для анализа богатств Италии.
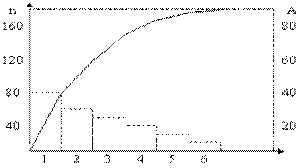
Рис. 10. Пример диаграммы Парето:
1 – ошибки в процессе производства; 2 – некачественное сырье;
3 – некачественные орудия труда; 4 – некачественные шаблоны;
5 – некачественные чертежи; 6 – прочее;
А – относительная кумулятивная (накопленная) частота, %;
n – число бракованных единиц продукции.
Приведенная диаграмма построена на основе группирования бракованной продукции по видам брака и расположения в порядке убывания числа единиц бракованной продукции каждого вида. Диаграмму Парето можно использовать очень широко. С ее помощью можно оценить эффективность принятых мер по улучшению качества продукции, построив ее до и после внесения изменений.
4. Причинно-следственная диаграмма
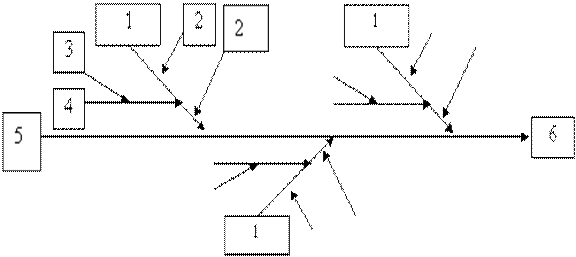
Рис. 11. Причинно-следственная диаграмма
а) пример условной диаграммы, где:
1 – факторы (причины); 2 – большая «кость»;
3 – малая «кость»; 4 – средняя «кость»;
5 – «хребет»; 6 – характеристика (результат).
б) пример причинно-следственной диаграммы факторов, влияющих на качество продукции
Рис. 12. Пример причинно-следственной диаграммы.
Причинно-следственная диаграмма используется, когда требуется исследовать и изобразить возможные причины определенной проблемы. Ее применение позволяет выявить и сгруппировать условия и факторы, влияющие на данную проблему.
Рассмотрим формупричинно-следственной диаграммы на рис. 12 (она называется еще «рыбий скелет» или диаграмма Исикавы).
Порядок составления диаграммы:
1. Выбирается проблема для решения – «хребет».
2. Выявляются наиболее существенные факторы и условия, влияющие на проблему – причины первого порядка.
3. Выявляется совокупность причин, влияющих на существенные факторы и условия (причины 2-, 3- и последующих порядков).
4. Анализируется диаграмма: факторы и условия расставляются по значимости, устанавливаются те причины, которые в данный момент поддаются корректировке..
5. Составляется план дальнейших действий.
5. Контрольный листок (таблица накопленных частот) составляется для построения гистограммы распределения, включает в себя следующие графы: (табл.2).
Таблица 2- Контрольный листок
| № интервала | Измеренные значения | Частота | Накопленная частота | Накопленная относительная частота |
На основании контрольного листка строится гистограмма (рис. 13), или, при большом количестве измерений, кривая распределения плотности вероятностей (рис. 14).
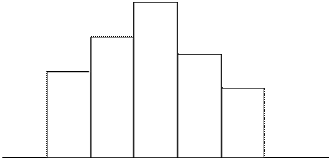
Рис. 13. Пример представления данных в виде гистограммы
Рис. 14. Виды кривых распределения плотности вероятностей.
Гистограмма представляет собой столбчатый график и применяется для наглядного изображения распределения конкретных значений параметра по частоте появления за определенный период времени. При нанесении на график допустимых значений параметра можно определить, как часто этот параметр попадает в допустимый диапазон или выходит за его предел.
При исследовании гистограммы можно выяснить, в удовлетворительном ли состоянии находятся партия изделий и технологический процесс. Рассматривают следующие вопросы:
- какова ширина распределения по отношению к ширине допуска;
- каков центр распределения по отношению к центру поля допуска;
- какова форма распределения.
6. Диаграмма разброса (рассеяния) применяется для выявления зависимости (корреляции) одних показателей от других или для определения степени корреляции между n парами данных для переменных x и y:
(x1,y1), (x2,y2),..., (xn, yn).
Эти данные наносятся на график (диаграмму разброса), и для них вычисляется коэффициент корреляции по формуле
,
,
,
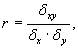
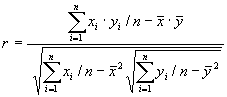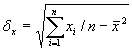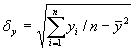где
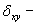ковариация; 
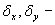стандартные отклонения случайных переменных x и у;n – размер выборки (количество пар данных – хi и уi); 
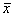и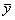 
– среднеарифметические значения хi и уi cоответственно.
Рассмотрим различные варианты диаграмм разброса (или полей корреляции) на рис. 15:
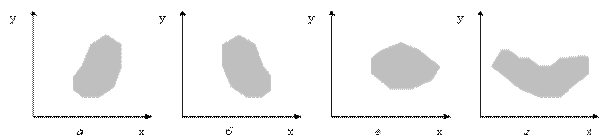
Рис. 15. Варианты диаграмм разброса
В случае:
а) можно говорить о положительной корреляции (с ростом x увеличивается y);
б) проявляется отрицательная корреляция (с ростом x уменьшается y);
в) при росте x y может как расти, так и уменьшаться, говорят об отсутствии корреляции. Но это не означает, что между ними нет зависимости, между ними нет линейной зависимости. Очевидная нелинейная (экспоненциальная) зависимость представлена и на диаграмме разброса г).
Коэффициент корреляции всегда принимает значения в интервале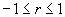 
, т.е. при r>0 – положительная корреляция, при r=0 – нет корреляции, при r <0 – отрицательная корреляция.
Для тех же n пар данных (x1,y1), (x2,y2),..., (xn, yn) можно установить зависимость между x и y. Формула, выражающая эту зависимость, называется уравнением регрессии (или линией регрессии), и ее представляют в общем виде функцией
у = а + bх.
Для определения линии регрессии (рис.4.19) необходимо статистически оценить коэффициент регрессии b и постоянную a. Для этого должны быть выполнены следующие условия:
1) линия регрессии должна проходить через точки (x,y) средних значений x и y.
2) сумма квадратов отклонений от линии регрессии значений y по всем точкам должна быть наименьшей.
3) для расчета коэффициентов а и b используются формулы
.
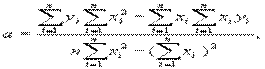
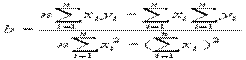Т.е. уравнением регрессии можно аппроксимировать реальные данные.
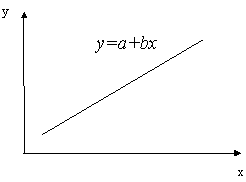
Рис. 16. Пример линии регрессии
7. Контрольная карта.
Одним из способов достижения удовлетворительного качества и поддержания его на этом уровне является применение контрольных карт. Для управления качеством технологического процесса необходимо иметь возможность контролировать те моменты, когда выпускаемая продукция отклоняется от заданных техническими условиями допусков. Рассмотрим простой пример. Проследим за работой токарного станка в течение определённого времени и будем измерять диаметр детали, изготавливаемой на нем (за смену, час). По полученным результатам построим график и получим простейшую контрольную карту (рис. 17):
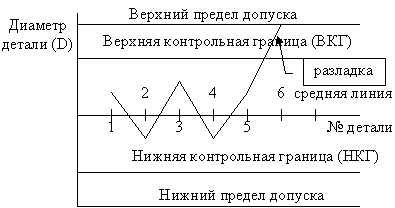
Рис. 17. Пример контрольной карты
В точке 6 произошла разладка технологического процесса, необходимо его регулирование. Положение ВКГ и НКГ определяется аналитически либо по специальным таблицам и зависит от объёма выборки. При достаточно большом объеме выборки пределы ВКГ и НКГ определяют по формулам
ВКГ = +3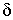 
,
НКГ = –3 ,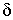
.
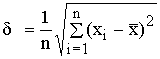ВКГ и НКГ служат для предупреждения разладки процесса, когда изделия еще соответствуют техническим требованиям.
Контрольные карты применяются, когда требуется установить характер неисправностей и дать оценку стабильности процесса; когда необходимо установить, нуждается ли процесс в регулировании или его необходимо оставить таким, каков он есть.
Контрольной картой можно также подтвердить улучшение процесса.
Контрольная карта является средством распознания отклонений из-за неслучайных или особых причин от вероятных изменений, присущих процессу. Вероятные изменения редко повторяются в прогнозируемых пределах. Отклонения из-за неслучайных или особых причин сигнализируют о том, что некоторые факторы, влияющие на процесс, необходимо идентифицировать, расследовать и поставить под контроль.Контрольные карты основываются на математической статистике.
Существуют два основных типа контрольных карт: для качественных (годен – негоден) и для количественных признаков. Для качественных признаков возможны четыре вида контрольных карт: число дефектов на единицу продукции; число дефектов в выборке; доля дефектных изделий в выборке; число дефектных изделий в выборке. При этом в первом и третьем случаях объем выборки будет переменным, а во втором и четвертом – постоянным.
Существуют следующие виды контрольных карт:
1. Контрольные карты для регулирования по количественным признакам (измеренные величины выражаются количественными значениями):
а) контрольная карта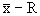 
состоит из контрольной карты 
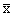, отражающей контроль за изменением среднего арифметического, и контрольной карты R, служащей для контроля изменений рассеивания значений показателей качества. Применяется при измерении таких показателей, как длина, масса, диаметр, время, предел прочности при растяжении, шероховатость, прибыль и т.д.;
б) Контрольная карта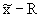 
состоит из контрольной карты 
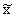, осуществляющей контроль за изменением значения медианы, и контрольной карты R. Применяется в тех же случаях, что и предыдущая карта. Однако она более проста, поэтому более пригодна для заполнения на рабочем месте.
2. Контрольные карты для регулирования по качественным признакам:
а) контрольная карта p (для доли дефектных изделий) или процента брака, применяется для контроля и регулирования технологического процесса после проверки небольшой партии изделий и разделения их на доброкачественные и дефектные, т.е. определения их по качественным признакам. Доля дефектных изделий получена путём деления числа обнаруженных дефектных изделий на число проверенных изделий. Может применяться также для определения интенсивности выпуска продукции, процента неявки на работу и т.д.;
б) контрольная карта pn (количество брака), применяется в случаях, когда контролируемым параметром является число дефектных изделий при постоянном объеме выборки n. Практически совпадает с картой p;
в) контрольная карта c (число дефектов на одно изделие), используется, когда контролируется число дефектов, обнаруживаемых среди постоянных объемов продукции (автомобили – одна или 5 транспортных единиц, листовая сталь – один или 10 листов);
г) контрольная карта n (число дефектов на единицу площади), используется, когда площадь, длина, масса, объём, сорт непостоянны и обращаться с выборкой как с постоянным объемом невозможно.
Выводы
Правильная организация контроля качества на предприятии, безусловно, играет очень важную роль.Успешность управления в компании зависит от того, насколько результативно осуществляется руководством контроль за деятельностью предприятия и насколько адекватны возникшие в результате этого контроля изменения в текущих бизнес-процессах компании.
Каждый процесс производства должен тщательно контролироваться и тогда предприятие сможет рассчитывать на высокий, а не приемлемый уровень качества.
На сегодняшний день важное значение предаётся внедрению на предприятии системы менеджмента качества ИСО 9001, которая направлена на достижение результатов, в соответствии с целями в области качества, чтобы удовлетворять потребности, ожидания и требования заинтересованных сторон. Система менеджмента качества даёт уверенность самой организации и потребителям в её способности поставлять продукцию, полностью соответствующую требованиям.
В данной главе также были рассмотрены основные методы, с помощью которых осуществляется контроль качества. Основу всех этих методов составляют статистические методы управления качеством.