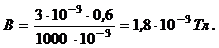Основные формулы
· Связь между индукцией и напряженностью магнитного поля:
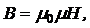
где m0 – магнитная постоянная, m0 = 4pּ10-7 Гн/м,
m –магнитная проницаемость среды.
· Закон Био-Савара-Лапласа:
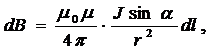
где dB – магнитная индукция поля, создаваемая элементом проводника длиной dl с током J; r – радиус-вектор, направленный от элемента проводника к точке, в которой вычисляется магнитная индукция; a - угол между радиус-вектором и направлением тока в элементе проводника.
· Магнитная индукция в центре кругового тока:
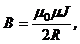
где R – радиус кругового витка.
· Магнитная индукция поля прямого тока:
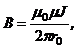
где r0 – расстояние от оси проводника до точки, в которой вычисляется магнитная индукция.
· Магнитная индукция поля, создаваемая отрезком провода с током J:
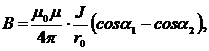
где a1 и a2 – углы между направлением тока и радиус – вектора, проведенные из начала и конца проводника в рассматриваемую точку.
· Напряженность магнитного поля внутри соленоида:
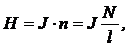
где п – число витков на единицу длины соленоида, N – общее число витков,
l – длина соленоида.
· Поток магнитной индукции, связанной с контуром:
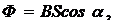
где S – площадь, ограниченная контуром, a – угол между нормалью к плоскости контура и направлением вектора магнитной индукции.
· На прямолинейный проводник длиной l c током J, находящийся в магнитном поле, действует сила Ампера:
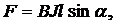
где a – угол между направлениями тока и вектора индукции.
· На заряженную частицу, движущуюся со скоростью n в магнитном поле, действует сила Лоренца:
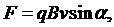
где q - заряд частицы, a - угол между направлением поля и скорости частицы.
· При перемещении проводника с током J в магнитном поле (перпендикулярно полю) совершается работа:
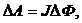
где D Ф – магнитный поток через площадь, описываемую проводником при перемещении.
· Закон Фарадея для электродвижущей силы индукции:
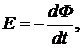
где 
– скорость изменения магнитного потока через площадь, ограниченную контуром.
· Возникающая в контуре ЭДС самоиндукции:
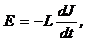
где L – индуктивность в контуре,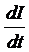 
– скорость изменения тока в контуре.
· Индуктивность соленоида:
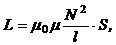
где N – число витков, S – площадь поперечного сечения соленоида, l – длина соленоида.
· Индуктивность контура L связана с пронизывающим его магнитным потоком Ф следующим соотношением:
,
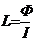где I – ток в контуре, обуславливающий магнитный поток.
· Энергия магнитного поля, создаваемого током I в контуре с и индуктивностью L:
.
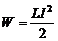· Плотность энергии магнитного поля:
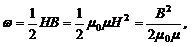
где Н – напряженность, В – индукция магнитного поля.
· ЭДС индукции, возникающая в рамке площадью S, содержащей N витков, при вращении ее с угловой скоростью w в магнитном поле с индукцией В, определяется соотношением:
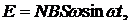
где wt – угол поворота рамки к моменту времени t.
Период собственных колебаний в контуре, не содержащим омическое сопротивление (ф.Томсона):
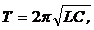
Полное сопротивление цепи переменного тока, содержащей последовательно соединенное омическое сопротивление R0, индуктивность L и емкость С:
.
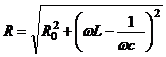Примеры решения задач
Задача №1
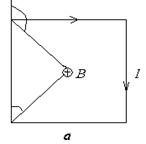Определите индукцию магнитного поля в центре проволочной квадратной рамки со стороной = 20 см, если по рамке течет ток 3А. 
Решение:
= 20 см=0,2 м Индукция магнитного поля в центре
I = 3A рамки равна векторной сумме индукций
______________ магнитного поля, создаваемых всеми её 
B -? сторонами: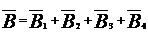 
.
Все эти векторы направлены в одну сторону перпендикулярно к плоскости рамки и вследствие симметрии B = 4B1
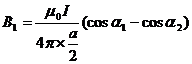, где 1=450, 2=1800-450=1350.
Окончательно имеем: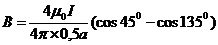 
.
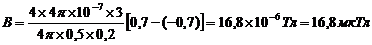Задача №2
Катушка длиной l = 40 см и диаметром 5 см содержит 300 витков. По катушке течет ток I = 1A. Определите: 1) индуктивность катушки; 2) магнитный поток, пронизывающий площадь её поперечного сечения.
Решение:
l=40 cм=0,4м 1) Индуктивность соленоида:
d=5cм=5*10-2м L=μ0 μ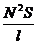 
. (1)
N=300 витков Площадь поперечного сечения:
I=1A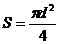 
. (2)
μ0= 4π *10-7Гн /м С учетом (2) индуктивность: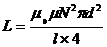 
, (3)
1) L-? 2)Ф -?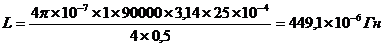 
2) Магнитный поток: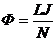 
, (4)
.
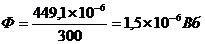Задача №3
В однородном магнитном поле с индукцией В = 0,1 Тл равномерно с частотой n = 600 мин-1 вращается рамка, содержащая 1000 витков, плотно прилегающих друг к другу. Площадь рамки 200 см2. Ось вращения лежит в плоскости рамки и перпендикулярна направлению магнитной индукции. Определите максимальную ЭДС, индуцируемую в рамке.
Решение:
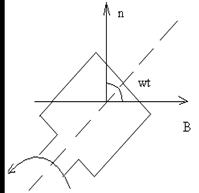
B = 0,1 Тл ЭДС по закону Фарадея:
n = 600 об/мин=10 об/с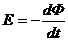 
. (1)
N = 1000 витков Магнитный поток:
S = 200 см2=2 ּ 10-2м2
_________________ 
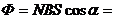
E max -?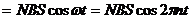 
(2)
Подставив (2) в (1), получим:
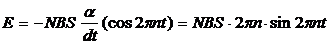. (3)
Emax – при sin 2πnt=1.
Emax=2πnNBS; Emax=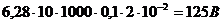 
.
Задача №4
По обмотке соленоида индуктивностью L = 3 мГн, находящегося в диамагнитной среде, течет ток I = 0,4 А. Площадь поперечного сечения S = 10 см2 и число витков N = 1000. Определить внутри соленоида: 1)энергию магнитного поля; 2) магнитную индукцию.
Решение
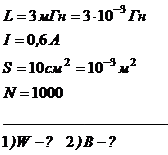1) Энергия магнитного поля: 
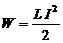, (1)
.
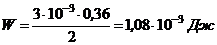2) Индукция магнитного поля соленоида: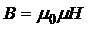 
, (2)
где Н – напряженность магнитного поля.
Зная индуктивность, можно определить магнитную проницаемость: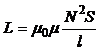 
,
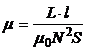, (3)
где l – длина соленоида.
Напряженность магнитного поля: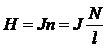 
. (4)
Подставив (4) и (3) в (2), получим: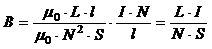 
. (5)
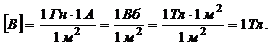
Вычислим В: 