1.1. От одной пристани до другой вниз по реке теплоход идет 8 ч. Возвращается он (против течения) за 10 ч. Скорость теплохода в стоячей воде νт = 18 км/ч. Определите расстояние между пристанями.
1.2. Свободно падающее тело в последнюю секунду своего падения проходит половину своего пути. Определите: 1) с какой высоты падало тело, 2) время падения.
1.3. За последнюю секунду свободно падающее без начальной скорости тело пролетело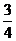 
всего пути. Сколько времени падало тело?
1.4. С башни высотой 25 м горизонтально брошен камень со скоростью 15 м/с. Найти: 1) сколько времени камень будет в движении, 2) на каком расстоянии Ѕx от основания башни он упадет на землю, 3) с какой скоростью он упадет на землю?
1.5. Зависимость пройденного телом пути S от времени дается уравнением S = A + Bt + Ct² + Dt³, где A = 0,1 м, B = 0,12 м/c², С = 0,2 м/с2 и D = 0,01 м/с³. Через, сколько времени после начала движения ускорение тела будет равно 1,6 м/с²?
1.6. Тело массой 1кг движется прямолинейно согласно уравнению
S = A – Bt + Ct² – Dt³, где A = 1 м, B = 3 м/с, С = 6 м/с² и D = 1 м/с³. Определите скорость и ускорение в конце первой секунды.
1.7. Движение материальной точки задано уравнением S = 4t + 0,05t³ (S – в метрах, t – в секундах). Определите ускорение точки в момент времени t1 = 2 c и t2 =10 c. Определите также среднее значение ускорения точки в промежутке времени от t1 до t2.
1.8. Зависимость пройденного телом пути от времени задается уравнением S = A + Ct2 + Dt3, где А = 1 м/с, С = 0,1 м/с2 и D = 0,03 м/с3. Определите:
1) время после начала движения, через которое ускорение будет равно 2 м/с2., 2) среднее ускорение <а> тела за этот промежуток времени.
1.9. Движение тела массой 0,5кг задано уравнением S = 2 + 3t + 6t3 (S – в метрах t – в секундах). Найти: 1) зависимость скорости и ускорения от времени, 2) силы, действующие на тело в конце второй и пятой секунд.
1.10. Вагон движется равнозамедленно с отрицательным ускорением 0,75 м/с2. Начальная скорость 54 км/ч.
Через сколько времени и на каком расстоянии от начальной точки вагон остановится?
1.11. Тело А начало движение с начальной скоростью ν'0 = 2 м/с и движется с постоянным ускорением а. Через 10 с из этой же точки начнёт движение тело В с начальной скоростью ν"0 = 12,5 м/с и тем же ускорением а.
Какова наибольшая величина ускорения а, при котором тело В сможет догнать тело А?
1.12. Два автомобиля начали движение одновременно в одном направлении из одного пункта. Зависимость пройденного пути задано уравнениями S1 = At + Bt2 + Ct3 и S2 = Dt + Et2. Определите относительную скорость автомобилей спустя 10 с после начала движения. (А = 10 м/с, В = 0,5 м/с2, С = 0,1 м/с3, D = 5 м/с, Е = 2 м/с2).
1.13. Тело движется равноускоренно с начальной скоростью ν0. Определите ускорение тела, если за время t = 3 с оно прошло путь S =18 м и его скорость оказалась равной 3ν0.
1.14. Уравнения движения двух материальных точек имеют вид x1 = At + Bt2 + Ct3 и x2 = Dt + Et2 + Ft3, где В = 8 м/с2, С = –3 м/с3, Е = – 4 м/с2, F = 1 м/с3. Определите момент времени, для которого ускорения этих точек будут равны.
1.15. Маховик вращается с постоянным угловым ускорением 3,14 рад/с2. Найти угловую скорость маховика через 25 полных оборотов.
1.16. Колесо, вращаясь равноускоренно, достигло угловой скорости ω = 20 рад/с через 10 оборотов после начала вращения. Найти угловое ускорение колеса.
1.17. Колесо, спустя 30 с после начала вращения приобретает скорость, соответствующую 720 об/мин. Найти угловое ускорение колеса и число сделанных оборотов за 30 с. Движение равноускоренное.
1.18. Вентилятор вращается с частотой 900 об/мин. После выключения вентилятор, вращаясь равнозамедленно, сделал до остановки 80 оборотов. Сколько времени прошло с момента выключения вентилятора до полной остановки?
1.19. Вал вращается с постоянной частотой 180 об/мин. С некоторого момента времени вал тормозится и начинает вращаться равнозамедленно с ε = 2 рад/с2. Определите: 1) через сколько времени вал остановится? 2) сколько оборотов сделает вал до остановки?
1.20. Колесо радиусом R = 20 см вращается с постоянным угловым ускорением ε = 3 рад/с2. Найти для точек на ободе колеса к концу первой секунды после начала движения: 1) угловую скорость, 4)линейную скорость, 3) тангенциальное ускорение, 4) нормальное ускорение.
1.21. Колесо радиусом 15 см вращается с постоянным угловым ускорением ε = 2 рад/с2. Найти для точек, лежащих на ободе колеса к концу десятой секунды тангенциальное, нормальное и полное ускорение.
1.22. Измельчитель кормов «Волгарь – 5» имеет барабан диаметром 450 мм. Угол поворота барабана после его включения изменяется по закону φ=At2+B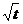 
, где А = 0,18 рад/с2иВ = 15 рад·с½. Найти угловую скорость вращения барабана через 25 с после начала вращения и линейную скорость точек на поверхности барабана.
1.23. Диаметр молотильных барабанов комбайна СКД – 5 равен 550 мм. Число оборотов барабанов регулируется вариатором в пределах 430÷1390. В каких пределах изменяется линейная скорость точек барабана, лежащих на его поверхности?
1.24. Битер льноуборочного комбайна вращается с постоянным угловым ускорением 2,5 рад/с2. Определите полное ускорение битера через 1 с после начала движения. Диаметр битера 450 мм.
1.25. Через неподвижный блок перекинута нить, к концам которой подвешены гири массой 5 и 3 кг. Определите силу натяжения нити и ускорение при движении гирь. Весом блока и трением пренебречь.
1.26. Два грузика с массами m1 = 300 г и m2 = 200 г соединены нитью, перекинутой через блок, подвешенный на пружинных весах. Определите ускорение грузов, показание пружинных весов и натяжение нити. Трением в оси блока и его массой пренебречь.
1.27. Автомобиль массой m = 5 т движется с постоянной скоростью ν =10 м/с: a) по выпуклому мосту, б) по вогнутому мосту. С какой силой нормального давления действует автомобиль на мост в его средней части? Радиус кривизны моста R = 50 м.
1.28. Велосипедист массой 80 кг движется со скоростью 10 м/с по выпуклому мосту радиуса 25 м. Определите силу упругости, действующую на велосипедиста в верхней точки моста.
1.29. Определите радиус R горбатого моста, имеющего вид дуги окружности, при условии, что давление автомобиля, движущегося со скоростью 90 км/ч, в верхней точке моста уменьшилось вдвое.
1.30. Масса автомобиля ГАЗ-24 – 1820 кг. Во время движения на автомобиль действует сила трения, равная 0,1 его веса. Чему должна быть равна сила тяги, развиваемая мотором автомобиля, чтобы он двигался с ускорением 2 м/с2?
1.31. Тело массой 1кг движется прямолинейно согласно уравнения
S = A – Bt + Ct2 – Dt3, где А = 1 м, В = 3 м/с, С = 5 м/с2 и D = 1 м/с3. Определите силу, действующую на тело в конце первой секунды.
1.32. Тело, массой m=2 кг двигалось под действием постоянной силы по закону S = A – Bt + Ct2 – Dt3, где В = 3 м/с, С = 5 м/с2 и D = 1 м/с3. Определите мощность N, затраченную на движение тела за время t = 1 c.
1.33. Трактор с сельскохозяйственной машиной испытывает тяговое сопротивление 40кН. При работе трактор имел среднюю скорость 4,6 км/ч. Определите работу, совершенную трактором за 6 ч.
1.34. Ведро с водой массой 8 кг подняли из колодца глубиной 10 м равноускоренно за 3,6 секунды. Определите величину совершенной при этом работу.
1.35. Пуля массой 10 г вылетевшая из винтовки с начальной скоростью ν0=1000 м/с, упала на землю со скоростью 400 м/с. Какая работа была затрачена во время полёта на преодоление силы сопротивления воздуха?
1.36. Какую работу надо совершить, чтобы заставить движущееся тело массой 4 кг: 1) увеличить свою скорость от 2 м/с до 6 м/с, 2) остановиться при начальной скорости 8 м/с.
1.37. С башни высотой H = 25 м горизонтально брошен камень со скоростью 15 м/с. Найти кинетическую и потенциальную энергии камня спустя одну секунду после начала движения. Масса камня m = 0,2 кг. Сопротивление воздуха не учитывать.
1.38. Автомобиль массой 5200 кг движется с постоянной скоростью в гору с уклоном 5 м на каждые 100 м пути. Определите мощность, развиваемую двигателем. Коэффициент трения к = 0,07.
1.39. Определите мощность электродвигателя, если его ротор вращается с частотой n = 24 м/с, а момент силы равен M = 16 Н·м.
1.40. Тело массой m = 10 кг поднимается с ускорением а = 2 м/с2. Определите работу силы в течение первых пяти секунд.
1.41. Молекула массой m = 4,65·10-26 кг ударяется о стенку под углом 60 ° к нормали и под таким же углом отскакивает без потери скорости. Определите импульс, полученный при ударе, если скорость молекулы ν = 600 м/с.
1.42. Определите импульс Р, полученный при ударе о стенку шарика массой 150 г, если шарик двигался со скоростью ν = 8 м/с под углом α = 30 ° к плоскости стенки. Удар считать упругим.
1.43. Снаряд, летевший со скоростью 400 м/с разорвался на два осколка. Меньший осколок, масса которого составила 30 % от массы снаряда, полетел в обратную сторону со скоростью 200 м/с. Определите скорость большого осколка.
1.44. Орудие, жестко закрепленное на железнодорожной платформе, производит выстрел вдоль полотна железной дороги под углом α = 30⁰ к линии горизонта. Определите скорость отката платформы орудия, если снаряд вылетел со скоростью 500 м/с. Масса платформы с орудием 16 т, масса снаряда 50 кг.
1.45. Граната, летящая со скоростью ν = 10 м/с при взрыве разлетелась на два осколка. Большой осколок, масса которого составила 70 % массы всей гранаты, продолжал двигаться в том же направлении со скоростью 20 м/с. Определите скорость меньшего осколка.
1.46. Орудие, жестко закрепленное на железнодорожной платформе, производит выстрел вдоль полотна железной дороги под углом α = 30 ⁰ к линии гарнизона. Определите скорость отката платформы, если снаряд вылетел со скоростью 480 м/с. Масса платформы с орудием и снарядами m = 18 т, а масса снаряда m1 = 60 кг.
1.47. С неподвижной лодки массой 50 кг на берег прыгает человек, масса которого 80 кг и скорость 1 м/с. Определите с какой скоростью начинает двигаться лодка.
1.48. На пол с высоты 2 м падает мяч массой 150 г и упруго отскакивает на высоту 1,6 м. Определите переданный полу импульс.
1.49. Молотильный барабан вращается с частотой, соответствующей 1200 об/мин. Под действием постоянного тормозного момента Мт = 20 Н·м барабан останавливается в течение 3 минут. Определите момент инерции барабана.
1.50. Молотильный барабан вращается с частотой n = 20 c-1. Момент инерции барабана J = 30 кг·м2. Определите момент силы, под действием которого барабан остановится за время t = 120 с.
1.51. Маховое колесо с моментом инерции J = 300 кг·м2 вращается, делая 20 об/с. Через 60 с после того, как на колесо перестал действовать вращающий момент, оно остановилось. Определите момент сил трения и число оборотов сделанных колесом до полной остановки после прекращения действия сил.
1.52. Маховик массой 50 кг и радиусом 20 см был раскручен до частоты вращения 480 об/мин и затем предоставлен самому себе. Под влиянием трения он остановился через 50 с. Найти момент силы трения.
1.53. Шар радиусом R = 10 см и массой m = 15 кг вращается вокруг оси симметрии согласно уравнению φ = A + Bt2 + Ct3, где В = 2 рад/с2, С = – 0,2 рад/с3. Определите момент силы М для t = 3 c.
1.54. Человек, расставив руки, стоит на скамье Жуковского, вращающейся относительно вертикальной оси с частотой 1 об/с. Какова будет частота вращения, если человек прижмет руки к туловищу? Момент инерции туловища (без рук) 0,8 кг·м2; момент инерции рук в горизонтальном положении 1,6 кг·м2 и в вертикальном положении – 0,6 кг·м2. Момент инерции скамьи Жуковского 0,15 кг·м2.
1.55. На краю платформы в виде диска диаметром D = 2 м вращающейся по инерции вокруг вертикальной оси с частотой n1 = 6 об/мин, стоит человек массой 75 кг. Когда человек перешел в центр платформы, она стала вращаться с частотой n2 = 8 об/мин. Определите массу платформы. Момент инерции человека на краю платформы рассчитать как для материальной точки.
1.56. Платформа в виде диска радиусом 1,2 м вращается по инерции, делая 6 об/мин. На краю платформы стоит человек массой 75 кг. Определите частоту вращения платформы, если человек перейдёт в её центр. Момент инерции платформы 120 кг·м2. Момент инерции человека на краю платформы рассчитать как для материальной точки.
1.57. Определите скорость поступательного движения сплошного цилиндра, скатившегося с наклонной плоскости высотой h = 20 см.
1.58. Диск массой m = 1,8 кг катится без скольжения по горизонтальной плоскости со скоростью 2 м/с. Определите кинетическую энергию диска.
1.59. Обруч скатывается по наклонной плоскости без скольжения. Высота наклонной плоскости 0,5 м. Определите скорость обруча в момент скатывания с плоскости.
1.60. Шар массой 2 кг катится без скольжения по горизонтальной плоскости со скоростью 4 м/с. Определите его кинетическую энергию.
1.61. Шар массой 0,5 кг и диаметром 8 см катится без скольжения по горизонтальной плоскости, делая 4 об/мин. Определите кинетическую энергию шара.
1.62. Сколько времени будет скатываться без скольжения обруч с наклонной плоскости длинной 2 м и высотой 10 см?
1.63. Тонкий прямой стержень длинной 1 м прикреплён к горизонтальной оси, проходящий через его конец. Стержень отклонили на угол 60 ° от положения равновесия и отпустили. Определите линейную скорость нижнего конца стержня в момент прохождения через положение равновесия.
1.64. Определите линейную скорость движения центра масс шара, скатывающегося без скольжения с наклонной плоскости, высота которой h = 0,5 м. Начальная скорость шара равна нулю.
1.65. Тело массой 1кг под действием постоянной силы движется прямолинейно по закону S = 2t2 + 8t + 1. Определите его кинетическую энергию через 10с.
1.66. Кинетическая энергия вала, вращающегося с постоянной скоростью, соответствующей 6 об/с, равна 60Дж. Определите момент количества движения вала.
1.67. К катящемуся шару, масса которого 2 кг, приложили силу 2Н, под действием которой шар остановился, пройдя путь 1 м. Определите скорость, с которой двигался шар до начала торможения.
1.68. По горизонтальной поверхности катится диск со скоростью ν = 6 м/с. Определите коэффициент сопротивления, если диск, будучи предоставленным самому себе, остановился, пройдя путь 18 м.
1.69. Определите первую космическую скорость спутника Земли на высоте, равной радиусу Земли (Rз = 6400км).
1.70. Вычислить период обращения спутника на высоте 300 км над Землёй. Радиус Земли Rз = 6400 км.
1.71. Искусственный спутник Земли движется по круговой орбите на высоте h = 500 км. Определите скорость его движения.
1.72. На какой высоте h ускорение свободного падения вдвое меньше его значения на поверхности Земли?
1.73. Определите скорость v, угловую скорость ω и центростремительное ускорение для движения Земли вокруг Солнца. Расстояние между ними r= 1,5·1011 м.
1.74. Материальная точка совершает гармонические колебания с амплитудой 0,32 м. Круговая частота ω0 = 2πt, начальная фаза ω0 = π/6. Записать уравнение и вычислить максимальное ускорение колеблющейся точки.
1.75. Точка совершает гармонические колебания с амплитудой А=10 см и периодом Т=5 с. Определить для этой точки: 1) максимальную скорость, 2) максимальное ускорение.
1.76. Тело массой 0,025 кг совершает гармоническое колебание с амплитудой 0,04 м и частотой ν = 8с-1. Начальная фаза равна нулю. Определите полезную энергию и напишите уравнение гармонического колебания.
1.77. Материальная точка массой m = 10г совершает гармонические колебания по закону х = 0,1 cos (4πt + π/4), м. Определите полную энергию этой точки.
1.78. Найти отношение длин двух математических маятников, если отношение периодов их колебаний равно 1.5.
1.79. Определите период гармонических колебаний диска радиусом 18 см вокруг горизонтальной оси, отстоящей от центра масс на 5 см.
1.80. Определите период (Т) и частоту (ν) гармонических колебаний диска радиусом R=20 см около горизонтальной оси, походящей через середину радиуса диска перпендикулярно его плоскости.
1.81. Определите период гармонических колебаний математического маятника на Луне, если принять, что масса Луны в 81 раз меньше массы Земли, а радиус Земли в 3,7 раза больше радиуса Луны. Длина нити маятника l = 1 м.
1.82. К пружине подвешен груз Р =13 кг. Зная, что пружина под влиянием силы в 2 кг растягивается на 3 см. Определите период вертикальных колебаний груза.
1.83. Налетая на пружинный буфер, вагон массой m =16 т, двигавшийся со скоростью 0,5 м/с останавливается, сжав пружину на 7 см. Определите жесткость к пружины буфера.
1.84. Чтобы растянуть пружину на 5 см требуется сила F = 10-5 Н. Какая сила требуется, чтобы растянуть ту же пружину на 20 см? Какая работа совершается при этом?