Основные формулы
· Количество вещества однородного газа (в молях):
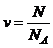 , или
, или 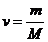 ,
,
где N – число молекул газа; NA – число Авогадро; m – масса газа; М – молярная масса газа.
· Уравнение Клапейрона-Менделеева (уравнение состояния газа):
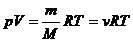 ,
,
где p – давление газа; V – его объем; T – температура; R – молярная газовая постоянная.
· Масса молекулы mi:
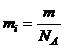
· Концентрация молекул (число молекул в единице объема) n0:
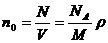 ,
,
где N – число молекул, содержащихся в данном объеме; r – плотность вещества.
· Средняя кинетическая энергия движения молекулы:
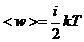 ,
,
где i - число степеней свободы; k - постоянная Больцмана.
· Основное уравнение кинетической теории газов:
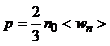 ,
, 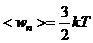 ,
,
где n0 – концентрация молекул; <wп> – средняя кинетическая энергия поступательного движения молекул.
· Зависимость давления газа от концентрации молекул n0 и температуры Т:
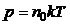 .
.
· Средняя квадратичная скорость молекулы:
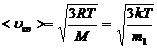 .
.
· Средняя арифметическая скорость молекулы:
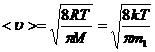 .
.
· Наиболее вероятная скорость молекулы:
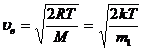 ,
,
где m1 – масса одной молекулы.
· Удельная теплоемкость газа при постоянном объеме (сv) и при постоянном давлении (ср):
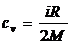 ;
; 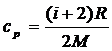 .
.
· Связь между удельной (с) и молярной (С) теплоемкостями:
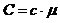 .
.
· Уравнение Роберта Майера:
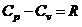 .
.
· Среднее число соударений молекул:
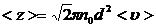 ,
,
где d – эффективный диаметр молекулы.
· Средняя длина свободного пробега молекулы:
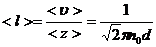 .
.
· Масса, переносимая при диффузии сквозь площадку D S за промежуток времени D t (закон Фика):
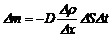 ,
,
где D – коэффициент диффузии; Dr /Dх – градиент плотности.
· Энергия, переносимая вследствие теплопроводности через площадку D S за промежуток времени D t (закон Фурье):
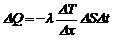 ,
,
где l – коэффициент теплопроводности; 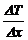 – градиент температуры.
– градиент температуры.
· Сила внутреннего трения F, действующая между слоями жидкости, пропорциональна площадке соприкасающихся двух слоев жидкости D S, градиенту скорости 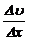 и коэффициенту внутреннего трения h (закон Ньютона):
и коэффициенту внутреннего трения h (закон Ньютона):
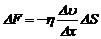 .
.
· Внутренняя энергия газа:
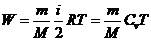 .
.
· Первое начало термодинамики:
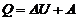 ,
,
где Q – теплота, сообщенная системе (газу); D U – изменение внутренней энергии системы; А – работа, совершаемая системой против внешних сил.
· Работа расширения газа:
а) при изобарном процессе: 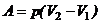 =
= 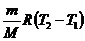 ;
;
б) при изотермическом процессе:
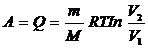 =
= 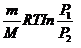
в) при адиабатном процессе:
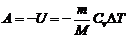 .
.
· Уравнение Пуассона для адиабатного процесса:
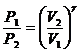 ,
, 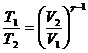 и
и 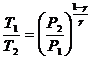
· Термический КПД идеальной тепловой машины:
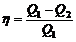 , или
, или 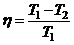 ,
,
где Q1 – теплота, полученная рабочим телом от нагревателя; Q2 – теплота, переданная рабочим телом охладителю; Т1 и Т2 – термодинамические температуры нагревателя и охладителя.
· Коэффициент поверхностного натяжения:
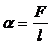 ,
,
где F – сила поверхностного натяжения, действующая на контур l, ограничивающий поверхность жидкости.
· Высота подъема жидкости в капиллярной трубке:
 ,
,
где Q - краевой угол; r - плотность жидкости; R – радиус трубки.
· Изменение энтропии системы при переходе из состояния А в состояние В: 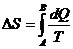 ,
,
где 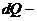 количество теплоты, переданное системой; Т - температура, при которой происходила теплопередача.
количество теплоты, переданное системой; Т - температура, при которой происходила теплопередача.
Примеры решения задач
Задача №1
Определить среднюю кинетическую энергию молекулы кислорода, находящейся при температуре 17°С. Найти также кинетическую энергию вращательного движения всех молекул, содержащихся в 4 г кислорода.
Решение:
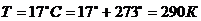 Средняя кинетическая энергия (поступательного
Средняя кинетическая энергия (поступательного
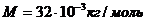 и вращательного движения) одной молекулы:
и вращательного движения) одной молекулы:
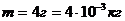
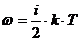 (1)
(1)
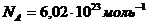 где
где 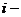 число степеней свободы, для двухатомного
число степеней свободы, для двухатомного
_____________________ газа 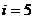 (
(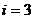 на поступательное движение и
на поступательное движение и 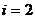
на вращательное движение); 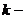 постоянная
постоянная
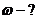
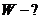 Больцмана,
Больцмана, 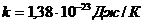 .
.
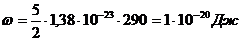 .
.
Кинетическая энергия вращательного движения всех молекул газа:
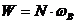 , (2)
, (2)
где 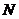 – число молекул:
– число молекул: 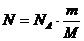 (3)
(3)
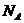
 число Авогадро;
число Авогадро;
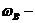 кинетическая энергия вращательного движения:
кинетическая энергия вращательного движения:
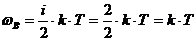 . (4)
. (4)
Подставив (3) и (4) в (2), получим: 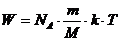 .
.
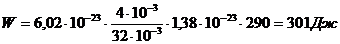 .
.
Задача №2
Азот массой m нагревается в одном случае изобарно, а в другом изохорно на D Т. Во сколько раз потребуется больше теплоты в первом случае, чем во втором?
Решение:
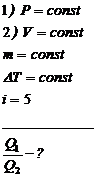 Теплота, потребляемая при изобарном процессе (P=const):
Теплота, потребляемая при изобарном процессе (P=const):
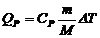 . (1) Теплота, потребляемая при изохорном процессе (V=const):
. (1) Теплота, потребляемая при изохорном процессе (V=const):
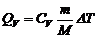 , (2)
, (2)
где СP и CV – молярные теплоемкости при постоянном давлении и объеме соответственно.
Поделив (1) на (2), получим:
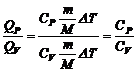 . (3)
. (3)
Так как
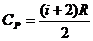 , (4)
, (4)
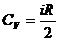 , (5)
, (5)
то подставив (4) и (5) в (3), получим:
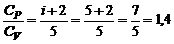 .
.
Таким образом, для любой массы газа при одинаковой разности температур отношения теплот есть величина постоянная.
Задача №3
Определите диаметр молекулы кислорода, если известно, что для кислорода коэффициент внутреннего трения при нормальных условиях равен 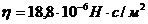 .
.
Решение:
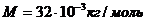 Коэффициент внутреннего трения:
Коэффициент внутреннего трения:
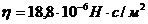
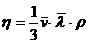 , (1)
, (1)
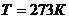
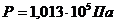 где
где 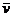 - средняя арифметическая скорость;
- средняя арифметическая скорость;
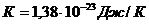
_________________ 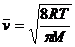 , (2)
, (2)
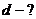
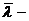 средняя длина свободного пробега молекулы
средняя длина свободного пробега молекулы
кислорода:
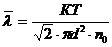 , (3)
, (3)
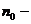 концентрация молекул:
концентрация молекул: 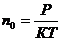 , (4)
, (4)
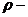 плотность кислорода:
плотность кислорода: 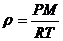 . (5)
. (5)
Подставив (2),(3),(4),(5) в уравнение (1), получим:
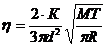 , откуда
, откуда 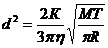 ,
,
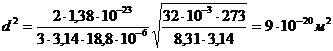 ,
, 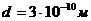 .
.
Задача №4
1 кг водорода нагрели до температуры 100 °С в условиях свободного расширения (P=const). Определите: 1) количество теплоты, сообщенное газу; 2) изменение его внутренней энергии; 3) работу расширения.
Решение:
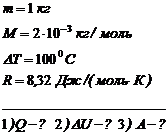 1) Количество теплоты Q, сообщенное водороду при P=const, определим по формуле:
1) Количество теплоты Q, сообщенное водороду при P=const, определим по формуле:
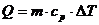 , (1)
, (1)
где ср – удельная теплоемкость газа при P=const.
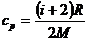 , (2)
, (2)
где i – число степеней свободы, для двухатомного газа i=5. Подставив (2) в (1), получим: 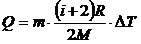 .
.
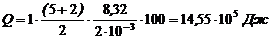 .
.
2) Внутренняя энергия газа выражается формулой:
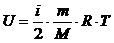 ,
,
а изменение внутренней энергии:
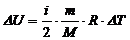 , (3)
, (3)
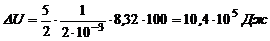 .
.
3) Работу расширения газа определим по формуле, выражающей первое начало термодинамики:
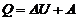 . (4)
. (4)
Откуда 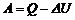 ,
,
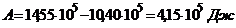 .
.
Задача№5
Азот, находящийся при температуре 27 °С и давлении в 1,5 атм, был адиабатически сжат до объема в 5 раз меньше начального объема. Определите давление и температуру азота после его сжатия.
Решение:
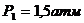 Давление после сжатия определим по формуле
Давление после сжатия определим по формуле
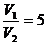 Пуассона:
Пуассона:
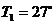
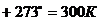
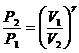 , откуда
, откуда 
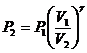 , (1)
, (1)
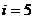 где
где 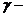 отношение теплоемкостей при постоянном
отношение теплоемкостей при постоянном
_________________ давлении и при постоянном объеме:
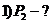
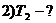
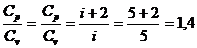 , (2)
, (2)
где 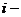 число степеней свободы,
число степеней свободы,
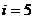 для двухатомного газа.
для двухатомного газа.
Температуру 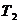 - после сжатия определим из формулы:
- после сжатия определим из формулы:
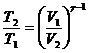 , откуда
, откуда 
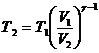 .
.
Произведем вычисления: 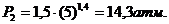
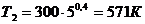 .
.