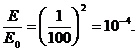· Согласно второму закону Ньютона:
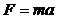 , или
, или 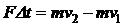 ,
,
где m - масса тела; а – ускорение, приобретенное им под действием силы F; v1 и v2 – начальная и конечная скорости.
· Закон сохранения импульса (количество движения):
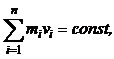
или для двух тел (i =2)
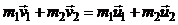 ,
,
где 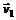 и
и 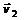 – векторы скоростей тел до взаимодействия;
– векторы скоростей тел до взаимодействия; 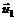 и
и 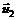 – векторы скоростей тех же тел после взаимодействия.
– векторы скоростей тех же тел после взаимодействия.
· Силы, рассматриваемые в механике:
а) сила тяжести: 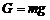 ;
;
б) сила трения скольжения: 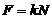 ,
,
где k – коэффициент трения скольжения; N - сила нормального давления.
в) сила упругости: 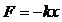 ,
,
где k – коэффициент упругости (жесткость пружины), х – абсолютная деформация;
г) сила гравитационного взаимодействия: 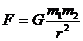 ,
,
где G – гравитационная постоянная; m1 и m2 - массы тел; r – расстояние между телами.
· Работа постоянной силы F на пути S:
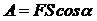 ,
,
где a – угол между направлением силы и пути.
· Мощность постоянной силы:
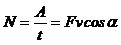 ,
,
где v – скорость движения.
· Кинетическая энергия тела массой m, движущегося поступательно со скоростью  ,
,
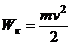 .
.
· Потенциальная энергия упруго деформируемого тела:
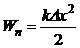 ,
,
где D х – величина деформации; k – коэффициент упругости.
· Потенциальная энергия тяготения двух шарообразных тел (или материальных точек) с массами m1 и m2:
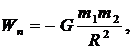
где R – расстояние между телами; G – гравитационная постоянная.
· Потенциальная энергия тела массой m, приподнятого на небольшую высоту h над землей:
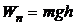 .
.
Динамика вращательного движения
· Момент силы F относительно некоторой оси вращения:
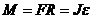 ,
,
где R – расстояние между линией действия силы и осью вращения; J – момент инерции; e – угловое ускорение.
· Моменты инерции некоторых тел массой m относительно оси, проходящей через центр масс:
а) диска (цилиндра): 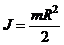 ,
,
где R - радиус диска (цилиндра);
|
|
б) материальной точки: 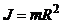 ;
;
в) тонкого стержня длиной l: 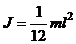 ;
;
г) шара с радиусом R: 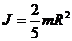 .
.
· Закон сохранения момента импульса:
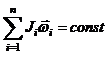 или для двух тел (i =2),
или для двух тел (i =2),
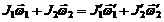 ,
,
где 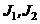 и
и 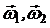 – моменты инерции тел и угловые скорости в начальный момент времени;
– моменты инерции тел и угловые скорости в начальный момент времени; 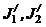 и
и 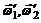 – в момент времени, принятый за конечный.
– в момент времени, принятый за конечный.
· Кинетическая энергия вращающегося тела:
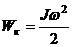 .
.
Примеры решения задач
Задача № 1
Зависимость пройденного телом пути от времени имеет вид 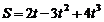 . Определите силу, действующую на тело с массой m=1 кг в конце второй секунды.
. Определите силу, действующую на тело с массой m=1 кг в конце второй секунды.
Решение:
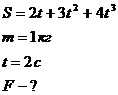 Сила, действующая на тело, по второму закону Ньютона
Сила, действующая на тело, по второму закону Ньютона
равна:

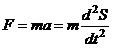 .
.
Мгновенное значение ускорения а определяется первой
производной от скорости по времени или второй производ-
ной от пути по времени:
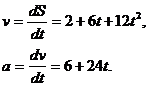
При t=2 с. 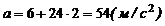 . Тогда
. Тогда 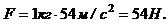
Задача №2
Тело массой 2 кг под действием постоянной силы движется прямолинейно так, что зависимость пройденного пути от времени выражается уравнением S=2t2+3t+1. Определите работу силы за 10 с сначала ее действия.
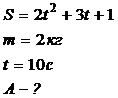 Решение:
Решение:
Работа, совершаемая силой, выражается через интеграл:
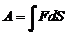 . (1)
. (1)
Сила, действующая на тело, по второму закону Ньютона:

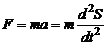 . (2)
. (2)
Мгновенное значение ускорения определяется первой производной от скорости по времени или второй производной пути по времени. В соответствии с этим получим:
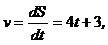 (3)
(3)
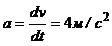 , (4)
, (4)
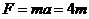 . (5)
. (5)
Тогда из формулы (3) имеем
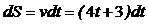 (6)
(6)
Подставив (5) и (6) в уравнение (1), получим:
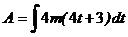
Работа, совершаемая силой за 10 с сначала движения, составит:
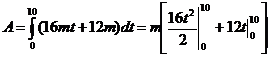
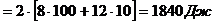 .
.
Задача №3
Диск радиусом R=10 см вращается так, что зависимость угла поворота диска от времени задается уравнением 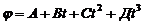
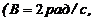
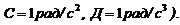 Определите для точек на ободе диска к концу второй секунды после начала движения:
Определите для точек на ободе диска к концу второй секунды после начала движения:
|
|
1) тангенциальное ускорение 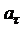 ;
;
2) нормальное ускорение 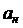 ;
;
3) полное ускорение 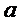 .
.
Решение:
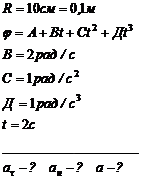 Найдем угловую скорость, взяв производную по времени от заданного уравнения:
Найдем угловую скорость, взяв производную по времени от заданного уравнения:
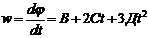 , при
, при 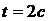
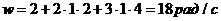 .
.
Угловое ускорение: 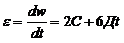 , при
, при 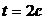
 .
.
Тангенциальное ускорение:
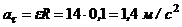 .
.
Нормальное ускорение: 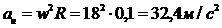 .
.
Полное ускорение: 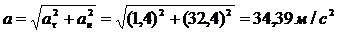 .
.
Задача №4
Шар радиусом R=10 см и массой m=15 кг вращается вокруг оси симметрии согласно уравнению 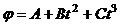
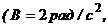 С = –0,2 рад/с3). Определите момент силы М для t=3 c.
С = –0,2 рад/с3). Определите момент силы М для t=3 c.
Решение:
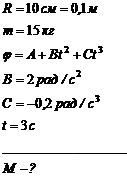 Момент силы согласно уравнению динамики вращательного движения:
Момент силы согласно уравнению динамики вращательного движения:

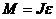 , (1)
, (1)
где J – момент инерции шара,
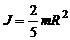 . (2)
. (2)
Угловое ускорение определяется первой производной от угловой скорости по времени или второй производной от угла поворота по времени:
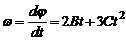 ,
,
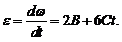 (3)
(3)
Подставив (2) и (3) в (1), получим:
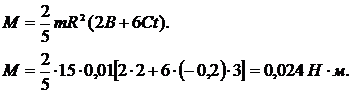
Задача №5
По горизонтальной поверхности катится диск со скоростью 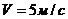 . Определите коэффициент сопротивления, если диск, будучи предоставленный самому себе, остановится, пройдя путь
. Определите коэффициент сопротивления, если диск, будучи предоставленный самому себе, остановится, пройдя путь 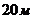 .
.
Решение:
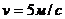 Кинетическая энергия диска:
Кинетическая энергия диска:
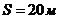
__________ 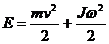 , (1)
, (1)
 где
где 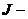 момент инерции диска,
момент инерции диска, 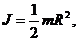
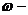 угловая скорость,
угловая скорость, 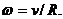
 . (2)
. (2)
Эта энергия пойдет на работу по преодоления сил сопротивления 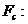
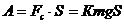 (3)
(3)
Приравнивая (2) и (3), получим:
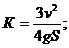
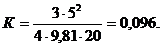
Задача №6
Радиус Луны  , а ее средняя плотность
, а ее средняя плотность 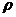
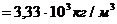 . Определите ускорение свободного падения на поверхности планеты.
. Определите ускорение свободного падения на поверхности планеты.
Решение:
 На всякое тело, расположенное вблизи
На всякое тело, расположенное вблизи
 поверхности планеты действует сила тяжести:
поверхности планеты действует сила тяжести:
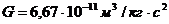
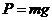 (1)
(1)
__________________ Ее можно приравнять к силе гравитационного
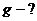 тяготения:
тяготения: 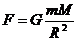 . (2)
. (2)
Откуда 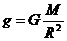 , (3)
, (3)
где 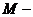 масса Луны,
масса Луны, 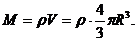 (4)
(4)
Подставив (4) в (3), получим: 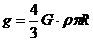 , (5)
, (5)
|
|
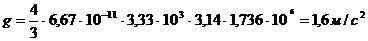 .
.
Задача №7
Логарифмический декремент затухания камертона,  колеблющегося с частотой
колеблющегося с частотой 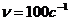 , равен
, равен 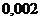 . Через какой промежуток времени амплитуда колебаний возбужденного камертона уменьшится в
. Через какой промежуток времени амплитуда колебаний возбужденного камертона уменьшится в 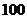 раз? Как изменится при этом энергия колебаний?
раз? Как изменится при этом энергия колебаний?
Решение:
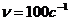 Амплитуда затухающих колебаний изменяется со временем
Амплитуда затухающих колебаний изменяется со временем
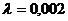 по закону:
по закону: 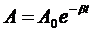 , (1)
, (1)
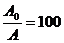 где
где 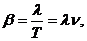
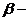 коэффициент затухания,
коэффициент затухания,
_________ 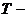 период колебаний,
период колебаний, 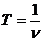 ,
,
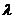 - логарифмический декремент затухания.
- логарифмический декремент затухания.
1) 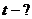 С учетом этого формулу (1) можно записать так:
С учетом этого формулу (1) можно записать так:
2) 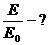
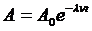 . (2)
. (2)
Откуда 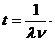
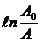 . (3)
. (3)
Энергия колебаний пропорциональна квадрату, произведения амплитуды и частоте колебаний: 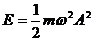 . (4)
. (4)
В данной задаче 
 поэтому
поэтому 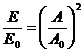 . (5)
. (5)
Проведем вычисления: 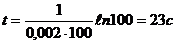 .
.