Основные формулы
По закону Кулона сила взаимодействия F между точечными зарядами Q1 и Q2, находящимися на расстоянии r один от другого в среде с диэлектрической проницаемостью e,
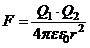 ,
,
где e0 = 8,85 10-12 Ф/м – электрическая постоянная.
· Напряженность электрического поля:
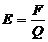 ,
,
где F – сила, с которой поле действует на пробный заряд Q.
· Напряженность поля точечного заряда Q, или поля вне равномерного заряженного шара:
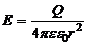 ,
,
где r – расстояние от заряда Q или от центра шара до точки, в которой определяется напряженность.
· Напряженность поля прямолинейной равномерно заряженной бесконечно длинной нити:
 ,
,
где t – линейная плотность заряда нити; r – расстояние от нити до точки, в которой определяется напряженность поля.
· Напряженность поля, образованного равномерно заряженной бесконечной плоскостью:
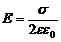 ,
,
где s – поверхностная плотность заряда плоскости.
· Разность потенциалов между двумя точками электрического поля определяется работой, совершаемой при перемещении единичного положительного заряда из одной точки плоя в другую:
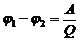 ,
,
где А – работа перемещения заряда Q.
· Потенциал поля точечного заряда:
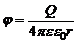 ,
,
где r – расстояние от заряда Q, создающего поле, до точки, в которой определяется потенциал.
· Для плоского конденсатора связь между напряженностью поля Е и разностью потенциалов U его пластин:
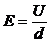 ,
,
где d – расстояние между пластинами.
· Электроемкость уединенного проводника:
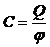 .
.
· Емкость плоского конденсатора:
 ,
,
где S - площадь пластины конденсатора.
· Емкость уединенного проводящего шара:
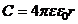 ,
,
где r – радиус шара.
· Емкость С системы конденсаторов связана с емкостями Сi, входящих в нее конденсаторов, соотношениями:
а) при последовательном соединении:
|
|
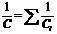 , или
, или 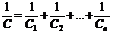 ;
;
б) при параллельном соединении:
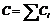 , или
, или 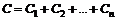
· Энергию W уединенного заряженного проводника можно определить по следующим формулам:
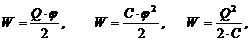
где Q, j и С – соответственно заряд, потенциал и емкость проводника.
Для плоского конденсатора
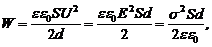
где S – площадь пластины; U – разность потенциалов между пластинами; s – поверхностная плотность заряда пластины; Е – напряженность электрического поля конденсатора.
· Плотность энергии электрического поля:
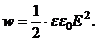
· Сила постоянного тока I связана с количеством электричества Q, проходящим через поперечное сечение проводника за время t, следующим соотношением:
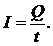
· Плотность тока:
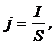
где S – площадь поперечного сечения проводника.
· Сопротивление проводника длиной l и площадью поперечного сечения S:
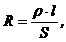
где r – удельное сопротивление материала проводника.
· Закон Ома для участка цепи:
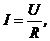
где U – разность потенциалов на концах участка; R – его сопротивление.
· Закон Ома для полной цепи:
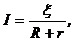
где x – электродвижущая сила источника тока; R – внешнее сопротивление цепи, r – внутреннее сопротивление источника тока.
· Удельное сопротивление r проводника связано с температурой t соотношением:
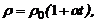
где r0 – удельное сопротивление при 0°С; a – температурный коэффициент сопротивления.
· Работа тока А на участке цепи (или количество теплоты, выделенное в нем при прохождении тока) определяется формулами:
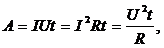
где t – время прохождения тока.
· Мощность тока, выделяемая на участке цепи, определяется соотношением:
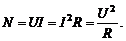
· Полная мощность, выделяемая в цепи:
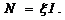
· Для расчета разветвленных цепей применяются два правила Кирхгофа.
|
|
Первое правило для алгебраической суммы токов в узле:

Второе правило для алгебраической суммы произведений токов на сопротивление участков и алгебраической суммы электродвижущих сил в контуре:
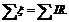
· Масса m вещества, выделившегося на электроде, пропорциональна химическому эквиваленту А/n, силе тока, протекающего через электролит, и времени прохождения тока:
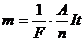 ,
,
где F – число Фарадея,
А – масса одного кг атома элемента,
n - валентность.

Примеры решения задач.
Задача №1
Два заряда Q1 = +8 нКл и Q2 = -6 нКл находятся в воздухе на расстоянии d = 8 см друг от друга. Определить напряженность и потенциал электрического поля в точке А, находящейся на расстоянии 10 см от каждого заряда.
 Решение:
Решение:
Напряженность электрического поля в точке А равна геометрической сумме напряженностей 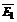 и
и 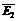 , создаваемых зарядами Q1 и Q2.
, создаваемых зарядами Q1 и Q2.


Модуль результирующей напряженности Е по теореме косинусов определяется как диагональ параллелограмма, построенного на векторах  и
и 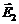 :
:
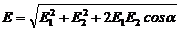 (1)
(1)
Абсолютные значения напряженностей и cosa определяем по формулам:
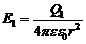 ,
,  (2)
(2)
По теореме косинусов:
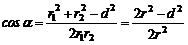 (3)
(3)
Подставив (2) и (3) в (1), получим:
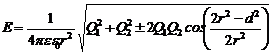 .
.
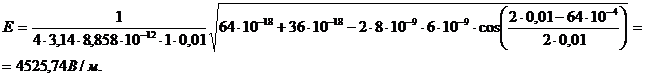
Потенциал электрического поля в точке А равен алгебраической сумме потенциалов j1 и j2 полей, создаваемых зарядами Q1 и Q2:
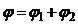 (4)
(4)
Потенциал поля точечного заряда
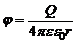 (5)
(5)
Подставив (5) в (4), получим:
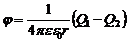 (6)
(6)
Вычислим:
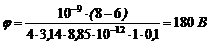 .
.
Задача №2
На помещенный между обкладками конденсатора заряд Q = 2,5 нКл действует сила F = 50 мкН. Площадь каждой пластины 100 см2, расстояние между пластинами d = 3 см. определить: 1) емкость конденсатора; 2) напряженность между обкладками; 3) разность потенциалов между обкладками; 4) энергию конденсатора; 5) объемную плотность энергии.
|
|
Решение:
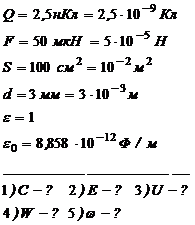 1). Емкость конденсатора:
1). Емкость конденсатора:
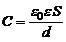 (1)
(1)
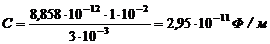
2). Напряженность между обкладками:
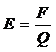 (2)
(2)
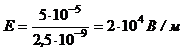 .
.
3). Разность потенциалов:
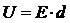 (3)
(3)
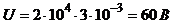 .
.
4). Энергия конденсатора:
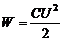 (4)
(4)
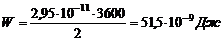 .
.
5). Объемная плотность энергии:
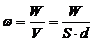 . (5)
. (5)
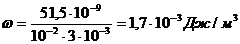 .
.
Задача №3
Сколько времени потребуется для нагревания воды массой 1,0 кг от начальной температуры 10 ⁰ С до кипячения в электрическом чайнике с нагревателем мощностью 800 Вт, если его КПД равен 90 %? Какова сила тока в электрической спирали, если напряжение в сети 220 В.
m=1,0 кг Решение:
t1 = 100C 1) Количество теплоты, необходимой для нагревания
t2 = 1000C воды: Q = cm(t2-t1)=cmΔ t. (1)
N = 800 Bт Она связана с мощностью нагревателя:
с = 4,2*10 3 Дж/кг*К Q=ηN t (2)
η = 90 % = 0,9 Приравняв (1) и (2), получим:
____________________ 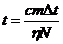 ,
,
1) t =? 2) I =? 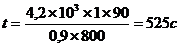 .
.
2) Сила тока: 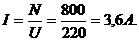
Задача№4
Внутреннее сопротивление аккумулятора 1 Ом. При силе тока 0,5 А его КПД равен 0,8. Определите ЭДС аккумулятора.
Решение:
r=1Ом КПД источника тока: 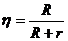 . (1)
. (1)
J=0,5А Отсюда 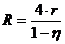 . (2)
. (2)
 Закон Ома для замкнутой цепи:
Закон Ома для замкнутой цепи: 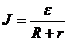 (3)
(3)
___________ Подставив (2) в (1), получим:
ε -? 
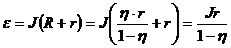 ;
; 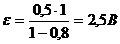 .
.
Задача№5
Два одинаковых источника тока соединены в одном случае последовательно, в другом параллельно и замкнуты на внешнее сопротивление 10 Oм. При каком внутреннем сопротивлении источника сила тока во внешней цепи будет в обоих случаях одинаковой?
Решение:
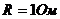 При последовательном соединении
При последовательном соединении 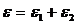 ,
,
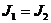 а внутреннее сопротивление
а внутреннее сопротивление 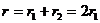 .
.
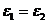 По закону Ома:
По закону Ома: 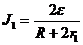
________ При параллельном соединении 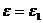 ,
,
 а внутреннее сопротивление
а внутреннее сопротивление 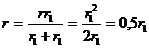
По закону Ома: 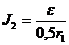
По условию 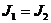 или
или 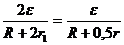 ;
; 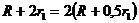 ,
, 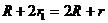 ,
,
Отсюда 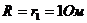 .
.