Новосибирский Государственный Аграрный Университет
Инженерный Институт
Ф И З И К А
Задачи для самостоятельного решения
Новосибирск 2020
Cоставители: М.Г.Алешкевич
Л.А.Митина
Физика. Методические указания к самостоятельной работе. Предназначены для студентов всех направлений подготовки и форм обучения реализуемых в НГАУ. / Новосиб. гос. аграр. ун-т. Инженерный институт. – Новосибирск. -2020. - 85 с.
Методические указания к самостоятельной работе составлены в соответствии с учебной программой, охватывают все разделы общей физики, а также даны задачи для решения по всем разделам. Для облегчения самостоятельной работы, перед каждым разделом приведены основные формулы и примеры решения задач, а в конце – справочные данные и ответы к задачам.
Утверждены и рекомендованы к изданию методическим советом Инженерного института, протокол № 9 от 22 апреля 2020 г.
Рецензент д.т.н., проф. С.В.Викулов (НГАВТ)
Ответственный за выпуск д.т.н., проф. А.П.Пичугин
ЗАДАНИЕ 1. Физические основы механики
Механика – часть физики, в которой рассматриваются закономерности движения и причины, вызывающие это движение. Данный материал является фундаментальным, т.к. понятия, закономерности, законы, содержащиеся в нем, применяются при изучении последующих разделов программы (законы Ньютона, закон сохранения энергии).
Для облегчения решения задач приведены основные формулы и примеры решения задач.
Поступательное движение
· Уравнения равномерного движения:
, 
, 
.
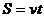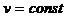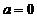· Уравнения равнопеременного движения:
, 
, 
.
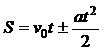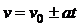· Уравнения неравномерного движения:
, 
, 
,
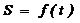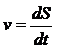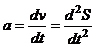где S – перемещение; n0 – начальная скорость; n – скорость в момент времени t;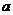 
– ускорение.
Вращательное движение
· Уравнения равномерного вращения:
, 
, 
.
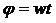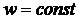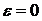· Уравнения равнопеременного вращения:
, 
, 
.
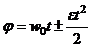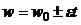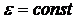· Уравнения неравномерного вращения:
, 
, 
.
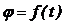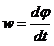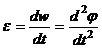где j – угловой путь, пройденный за время t; w0 – начальная угловая скорость; w – угловая скорость в момент времени t; e – угловое ускорение.
· Связь между угловой скоростью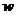 
, периодом Т и частотой вращения n:
.
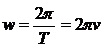· Связь между линейными и угловыми кинематическими величинами:
, 
, 
,
,
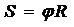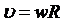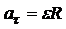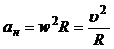где аt – тангенциальное ускорение; ан – нормальное ускорение; R – радиус окружности.
· Полное ускорение:
.
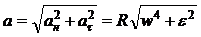Гармоническое колебательное движение. Волны
· Смещение колеблющейся точки:
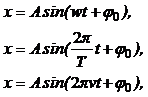
где x – смещение; А – амплитуда; w – круговая, или циклическая частота:
; 
,
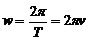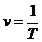где n – частота; j0 – начальная фаза.
· Скорость колеблющейся точки:
.
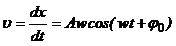· Ускорение колеблющейся точки:
.
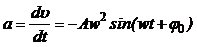· Возвращающаяся сила:
,
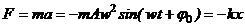где m – масса материальной точки;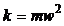 
– коэффициент возвращающейся силы.
· Кинетическая W к, потенциальная W п и полная W энергии гармонического колебания:
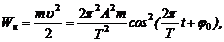
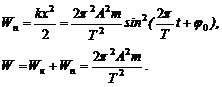
· Период колебания математического маятника:
,
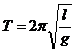где l – длина маятника; g – ускорение свободного падения.
· Период колебания пружинного маятника:
,
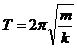где k – жесткость пружины.
· Период колебания физического маятника:
,
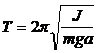где J – момент инерции маятника относительно оси вращения; а – расстояние от центра масс до оси вращения.
· Длина волны l, скорость n ее распространения и период Т связаны соотношением:
.
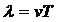· Уравнение волны:
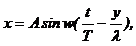
где А – амплитуда; Т – период; l – длина волны; х – смещение точки среды (участвующей в волновом процессе) в любой момент времени t; y – расстояние от этой частицы до источника волны.