· Момент количества движения (импульса) электрона в атоме на стационарной орбите:
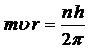 ,
,
где m – масса электрона; u – его линейная скорость; r – радиус орбиты; n – главное квантовое число; h – постоянная Планка.
· Радиус стационарной орбиты атома водорода:
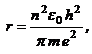
где е – заряд электрона; e0 – электрическая постоянная.
· Кинетическая, потенциальная и полная энергии электрона на орбите соответственно равны:
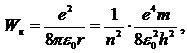
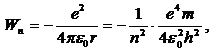
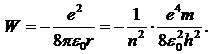
· Частота излучения атома водорода:
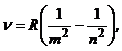
где R=3,28985×1015 с-1 – постоянная Ридберга; m – номер орбиты, на которую переходит электрон; n – номер орбиты, с которой переходит электрон.
· Частота излучения водородоподобного атома (иона):
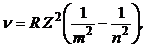
где Z – атомный номер элемента.
· Коротковолновая граница сплошного рентгеновского спектра определяется соотношением:
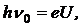
где n0 – частота, соответствующая коротковолновой границе; U – разность потенциалов, приложенная к рентгеновской трубке.
· Частота характеристического рентгеновского излучения:
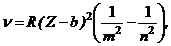
где Z – порядковый номер элемента, из которого сделан антикатод; b – постоянная экранирования.
· Закон Мозли:
· 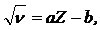
где 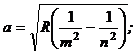 b – постоянная экранирования.
b – постоянная экранирования.
· Закон радиоактивного распада:
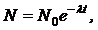
где N0 – число атомов в начальный момент времени; N – число атомов, оставшихся по истечении времени t; l - постоянная распада.
· Период полураспада Т связан с постоянной распада соотношением:
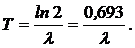
· Среднее время жизни атома радиоактивного вещества:
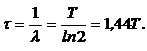
· Активность элемента:
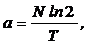
где N – число атомов элемента.
· Дефект массы атомного ядра:
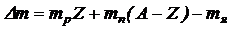 ,
,
где mр – масса протона; mn – масса нейтрона; mя – масса ядра; А – массовое число; Z – порядковый номер элемента.
· Энергия связи ядра:
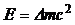 ,
,
где с – скорость света.
· Энергия связи, выраженная в мегаэлектронвольтах:
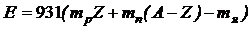
· Удельная энергия связи:
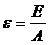 .
.
· Количество ядерной энергии DE, связанное с каждым прореагировавшим ядром, равно разности между энергией связи E2 продукта реакции и энергией связи исходного ядерного материала E1:
DE=E2 -E1
или
DE=931(m2-m1),
где m1 и m2 – массы атомов исходного материала и конечного продукта реакции. При DE>0 ядерная энергия выделяется, при DE<0 ядерная энергия поглощается.
Примеры решения задач
Задача№1
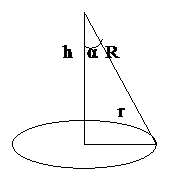
Над серединой круглого стола на высоте 2 м висит лампа в 400 к д. Определите освещенность в центре стола и на краю стола, если его диаметр равен 1м.
 Решение:
Решение:
h = 2 м 1) Освещенность в центре стола:
d = 1 м, r = 0,5 м
 J = 400 к д
J = 400 к д 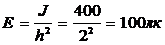 .
.
1) Е-? 2)Е-?
2) По теореме Пифагора определим R и cos 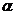 :
:
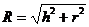 ,
, 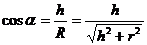
Освещенность на краю стола: 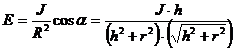 ;
;
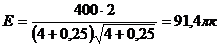 .
.
Задача №2
На дифракционную решетку нормально падает монохроматический свет с длиной l = 480 нм. Определите наибольший порядок спектра, полученный с помощью решетки и максимальный угол отклонения лучей, если ее постоянная d = 2 мкм.
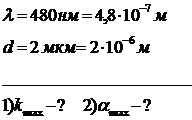 Решение
Решение
1). Для определения числа максимумов дифракционной решетки, примем во внимание, что максимальный угол отклонения лучей дифракционной решетки не может превышать 90 °. Тогда из формулы 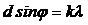 имеем
имеем
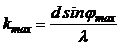 .
.
Подставляя заданные величины, имеем:
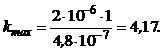
Поскольку k обязательно должно быть целым числом, принимаем 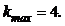
2). Максимальный угол отклонения лучей, соответствующий последнему дифракционному максимуму
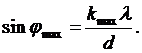
Подставляя численные значения, получим:
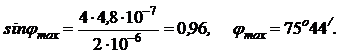
Задача №3
Максимум спектральной плотности энергетической светимости поверхности Солнца приходится на длину lmax=0,5мк. Определить:1) температуру поверхности Солнца; 2) полный поток излучения солнечной энергии; 3) световое давление на земную поверхность. Коэффициент отражения принять равным 0,6.
Решение:
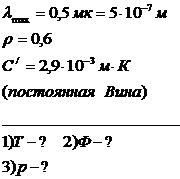 1) Приняв Солнце за черное тело, температуру
1) Приняв Солнце за черное тело, температуру
поверхности Солнца определим по закону
Вина:
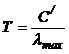 , (1)
, (1)
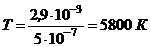 .
.
2) Полный поток излучения солнечной энергии, приходящейся на все длины волн (мощность излучния):
Ф =Rе × S,(2)
где Rе – энергетическая светимость черного тела по закону Стефана-Больцмана:
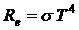 , (3)
, (3)
где s – постоянная Стефана-Больцмана, 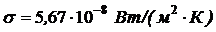 , S – площадь Солнца,
, S – площадь Солнца,
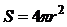 , (4)
, (4)
где r – радиус Солнца, r =6,95×108 м.
Полный поток излучения с учетом (3) и (4):
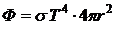 (5)
(5)
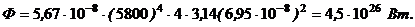
3) Световое давление р определим по формуле:
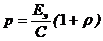 , (6)
, (6)
где Еэ – плотность потока энергии у поверхности Земли:
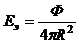 , (7)
, (7)
где R – среднее расстояние от Земли до Солнца.
Подставив (7) в (6), получим:
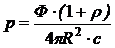 (8)
(8)
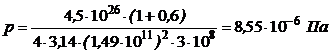 ,
,
Задача №4
Цезий освещается монохроматическим светом с длиной волны 400 нм. Определит наименьшее задерживающее напряжение, при котором фототок прекратиться. Работа выхода электронов из цезия равна 1.89 эВ.
Решение:
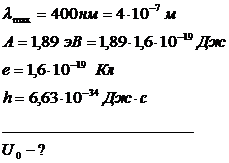 Уравнение Эйнштейна для фотоэффекта:
Уравнение Эйнштейна для фотоэффекта:
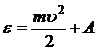 (1) или
(1) или 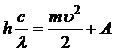 . (1/)
. (1/)
Для того чтобы ток прекратился, необходимо приложить задерживающее напряжение U0 , при
котором:
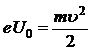 . (2)
. (2)
С учетом (2) уравнение (1) примет вид:
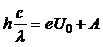 .
.
Откуда 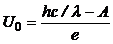 .
.
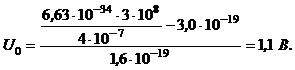
Задача №5
Определить длину волны и энергию фотона при переходе электрона в атоме водорода с четвертого энергетического уровня на второй (серия Бальмера).
Решение
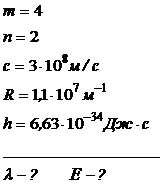 При переходе электрона с отдаленной орбиты на внутреннюю происходит излучение энергии:
При переходе электрона с отдаленной орбиты на внутреннюю происходит излучение энергии:
ε 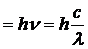 , (1)
, (1)
где ε – энергия фотона; h – постоянная Планка; с – скорость света; l – длина волны.
Величину, обратную длине волны, определим по формуле:
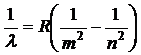 , (2)
, (2)
где R – постоянная Ридберга; m – номер орбиты, на которую переходит электрон; n – номер орбиты, с которой переходит электрон.
Подставив в (2) числовые значения, получим:
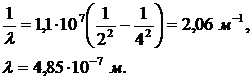
Подставив числовые значения в (1), получим:
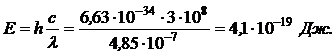
Задача №6
Радиоактивный натрий 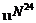 распадается с выбросом a-частиц. Период полураспада Т равен 14,8 ч. Определить: 10 количество атомов, распавшихся в 1 г данного радиоактивного препарата за 10ч.
распадается с выбросом a-частиц. Период полураспада Т равен 14,8 ч. Определить: 10 количество атомов, распавшихся в 1 г данного радиоактивного препарата за 10ч.
Решение
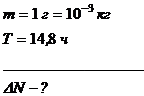 Число радиоактивных атомов убывает со временем по закону:
Число радиоактивных атомов убывает со временем по закону:

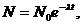 (1)
(1)
где N0 – число атомов в начальный момент времени; N – число атомов, оставшихся по истечении времени t;
l - постоянная распада:
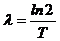 . (2)
. (2)
Число распавшихся атомов:
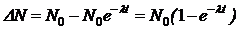 . (3)
. (3)
Выразив l через период полураспада Т, преобразуем выражение 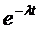 :
:
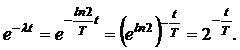
С учетом преобразования, (3) примет вид:
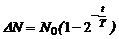 . (4)
. (4)
Определим N0. По определению 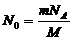 , (5)
, (5)
где NA – число Авогадро, NA=6,02×1023 моль-1; М – молярная масса, М=24×10-3 кг/моль.
С учетом (5) имеем:
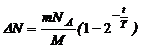 , (6)
, (6)
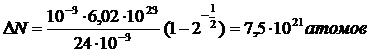
Задача №7
Вычислить энергию ядерной реакции
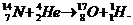
Выделяется или поглощается эта энергия?
Решение:
Энергию ядерной реакции определим по формуле:
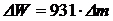 , (1)
, (1)
где Dm – изменение массы реакции, т.е. разность между массой частиц, вступивших в реакцию, и массой частиц, образовавшихся в результате реакции.
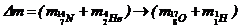 (2)
(2)
По таблице 11 находим массы этих частиц и вычисляем Dm
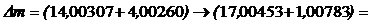
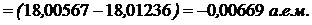
Тогда  .
.
Энергия поглощается, т.к. масса исходных ядер меньше массы ядер, образовавшихся в ходе реакции.