Статистическая гипотеза — это определённое предположение о распределении вероятностей, лежащем в основе наблюдаемой выборки данных.
Проверка статистической гипотезы — это процесс принятия решения о том, противоречит ли рассматриваемая статистическая гипотеза наблюдаемой выборке данных.
Статистический тест или статистический критерий — строгое математическое правило, по которому принимается или отвергается статистическая гипотеза.
1. Формулируется нулевая гипотеза 
о распределении вероятностей на множестве 
. Чаще всего рассматриваются две гипотезы — основная или нулевая и альтернативная 
. Иногда альтернатива не формулируется в явном виде; тогда предполагается, что означает «не ».
2. Задаётся некоторая статистика (функция выборки) 
, для которой в условиях справедливости гипотезы выводится функция распределения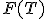 
и/или плотность распределения 
. Вопрос о том, какую статистику надо взять для проверки той или иной гипотезы, часто не имеет однозначного ответа. Есть целый ряд требований, которым должна удовлетворять «хорошая» статистика 
. Вывод функции распределения 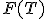при заданных и является строгой математической задачей, которая решается методами теории вероятностей; в справочниках приводятся готовые формулы для 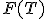; в статистических пакетах имеются готовые вычислительные процедуры.
3. Фиксируется уровень значимости — допустимая для данной задачи вероятность ошибки первого рода, то есть того, что гипотеза на самом деле верна, но будет отвергнута процедурой проверки. Это должно быть достаточно малое число 
. На практике часто полагают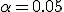 
.
4. На множестве допустимых значений статистики выделяется критическое множество 
наименее вероятных значений статистики , такое, что 
. Вычисление границ критического множества как функции от уровня значимости 
является строгой математической задачей, которая в большинстве практических случаев имеет готовое простое решение.
5. Собственно статистический тест (статистический критерий) заключается в проверке условия:
если 
, то делается вывод «данные противоречат нулевой гипотезе при уровне значимости ». Гипотеза отвергается.
если 
, то делается вывод «данные не противоречат нулевой гипотезе при уровне значимости ». Гипотеза принимается.
Итак, статистический критерий определяется статистикой .
По мере увеличения длины выборки нулевая гипотеза может сначала приниматься, но потом выявятся более тонкие несоответствия данных гипотезе, и она будет отвергнута. То есть многое зависит от объёма данных; если данных не хватает, можно принять даже самую неправдоподобную гипотезу.
Выбранная статистика может отражать не всю информацию, содержащуюся в гипотезе . В таком случае увеличивается вероятность ошибки второго рода — нулевая гипотеза может быть принята, хотя на самом деле она не верна. Допустим, например, что = «распределение нормально»;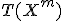 
= «коэффициент асимметрии»; тогда выборка с любым симметричным распределением будет признана нормальной. Чтобы избегать таких ошибок, следует пользоваться более мощными критериями.