Теорема. Если предпосылки 1 — 5 выполнены, то оценки, полученные по МНК, обладают следующими свойствами:
1. Оценки являются несмещенными, т.е. M[ b0 ] = b0, M[ b1 ] = b1. Это говорит об отсутствии систематической ошибки при определении положения линии регрессии.
2. Оценки состоятельны, т.к. при n ® µ D[ b0 ] ® 0, D[ b1 ] ® 0. Это означает, что с ростом n надежность оценок возрастает.
3. Оценки эффективны, т.е. они имеют наименьшую дисперсию по сравнению с любыми другими оценками данных параметров, линейными относительно величин yi.
20.Дисперсии и стандартные ошибки коэффициентов (ковариационная матрица и ее выборочная оценка)
Знание дисперсий и стандартных ошибок позволяет анализировать точность оценок, строить доверительные интервалы для теоретических коэффициентов, проверять соответствующие гипотезы. Наиболее удобно формулы расчета данных характеристик приводить в матричной форме.
Преобразуем вектор оценок 
с учетом наличия случайной составляющей:
,
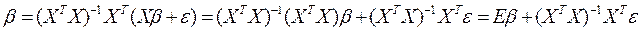Т.е. оценки параметров, найденные по выборке, будут содержать случайные ошибки.
Вариации оценок параметров будут определять точность уравнения множественной регрессии. Для их измерения в многомерном регрессионном анализе рассматривают ковариационную матрицу К, являющуюся матричным аналогом дисперсии одной переменной
, 
.
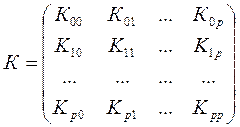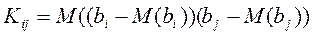Ковариация характеризует как степень рассеяния значений двух переменных относительно их математических ожиданий, так и взаимосвязь этих переменных. Так как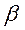 
является несмещенной оценкой, то
, 
.
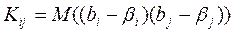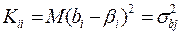В матричном виде будем иметь
,
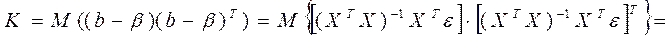
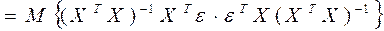
так как эти элементы Х – детерминированные величины.
В матрице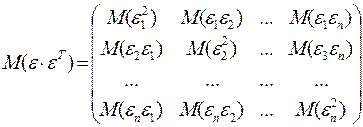 
все элементы, не лежащие на главной диагонали, равны нулю в силу некоррелируемости 
и 
между собой, а все элементы, лежащие на главной диагонали равны одной и той же дисперсии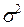 
: 
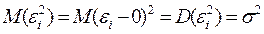. Поэтому 
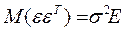и, следовательно, ковариационная матрица
.
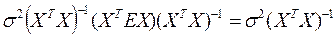Так как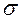 
2 неизвестна, заменив её несмещённой оценкой – выборочной дисперсией,
,
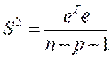где (n-p-1) – число степеней свободы, получим выборочную оценку ковариационной матрицы.
Интервальные оценки коэффициентов уравнения множественной регрессии. Проверка статистической значимости коэффициентов уравнения множественной регрессии.
Как и в случае парной регрессии, статистическая значимость коэффициентов множественной линейной регрессии с 
объясняющими переменными проверяется на основе 
-статистики:
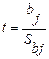
имеющей в данном случае распределение Стьюдента с числом степеней свободы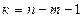 
. При требуемом уровне значимости наблюдаемое значение -статистики сравнивается с табличным значением распределения Стьюдента.
В случае, если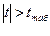 
, то статистическая значимость соответствующего коэффициента регрессии подтверждается. Это означает, что фактор 
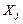линейно связан с зависимой переменной 
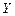. Если же установлен факт незначимости коэффициента 
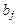, то рекомендуется исключить из уравнения переменную 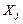. Это не приведет к существенной потере качества модели, но сделает ее более конкретной.